
Union of Sets
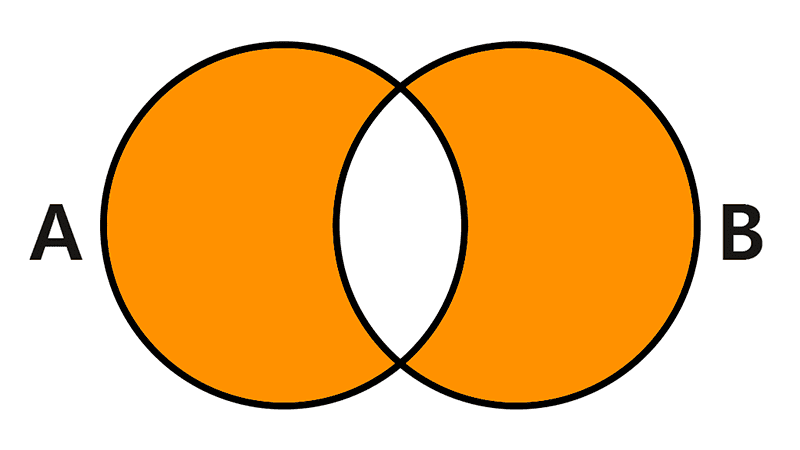
The union of sets is an operation that creates a new set containing all the elements from the original sets, without repeating common elements. It is represented by the symbol “∪”, similar to the letter U.
Formally, we define the union of two sets A and B as the set formed by the elements that belong to A, to B, or to both. It is denoted as A ∪ B and expressed in set-builder notation as:
A ∪ B = { x | x ∈ A ∨ x ∈ B }
We see that the definition uses an inclusive disjunction (the logical connective "or"), which is why an element will be part of the union if it belongs to one of the sets or to both simultaneously.
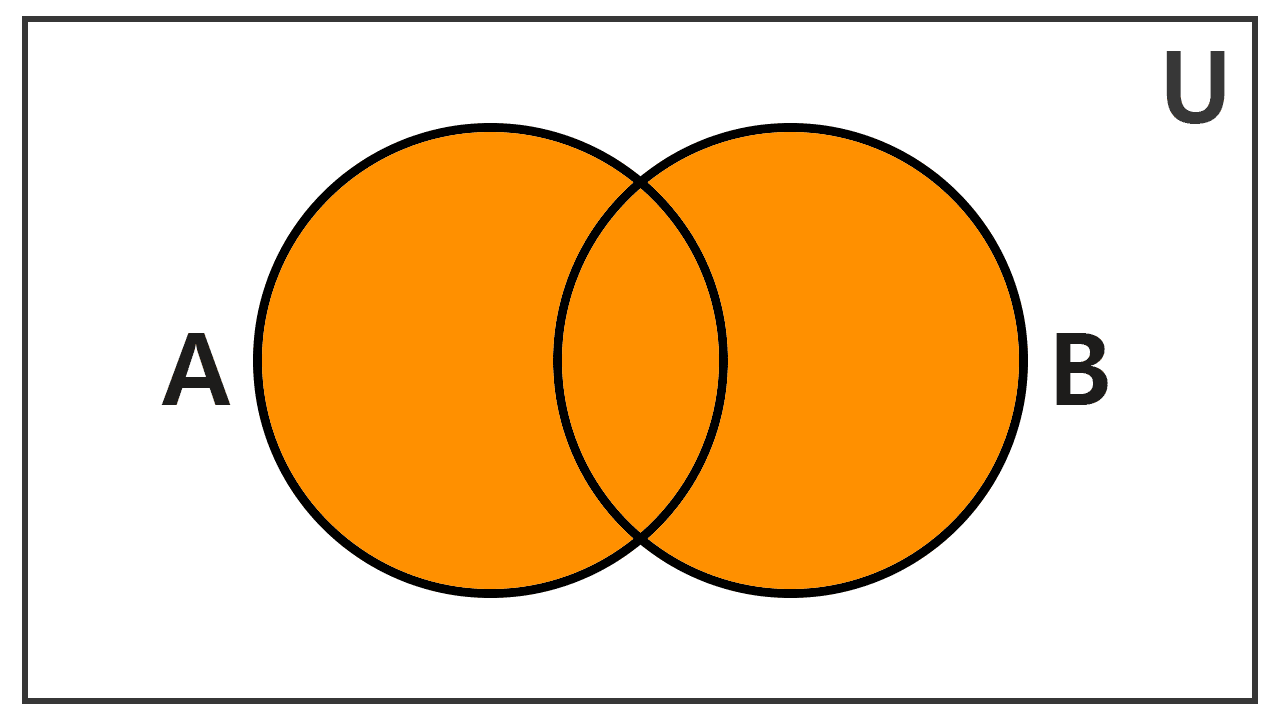
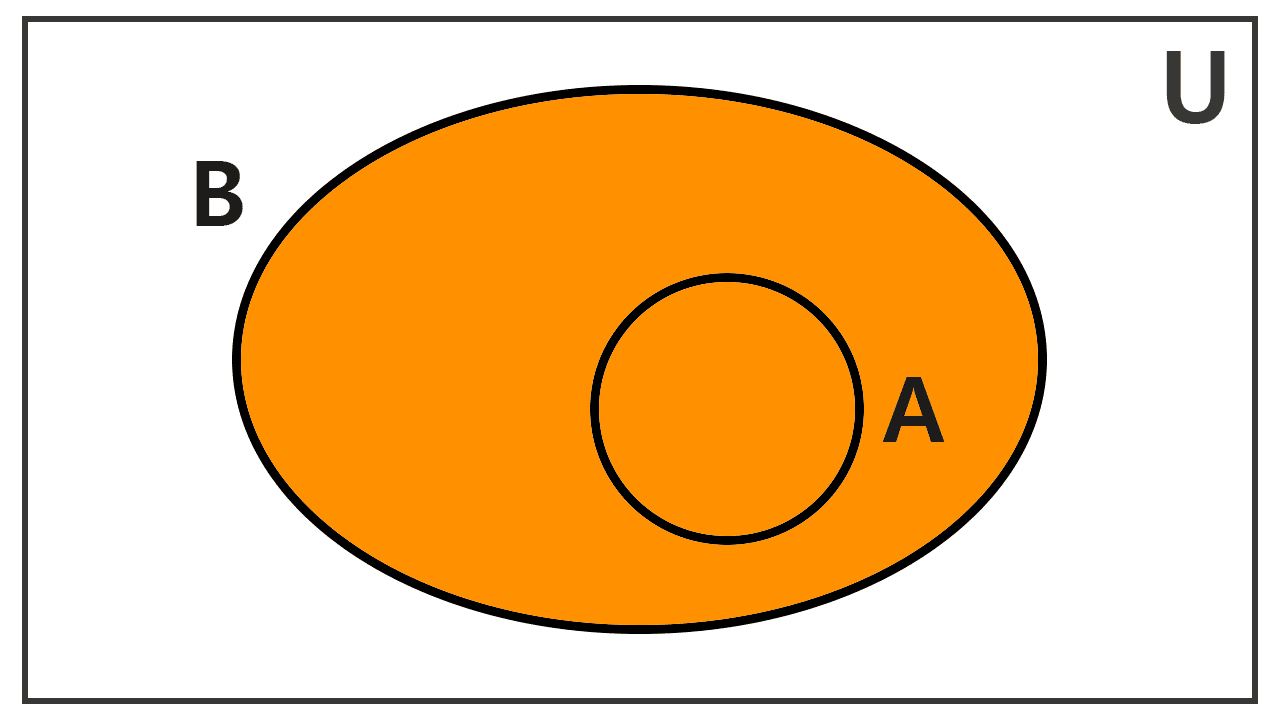
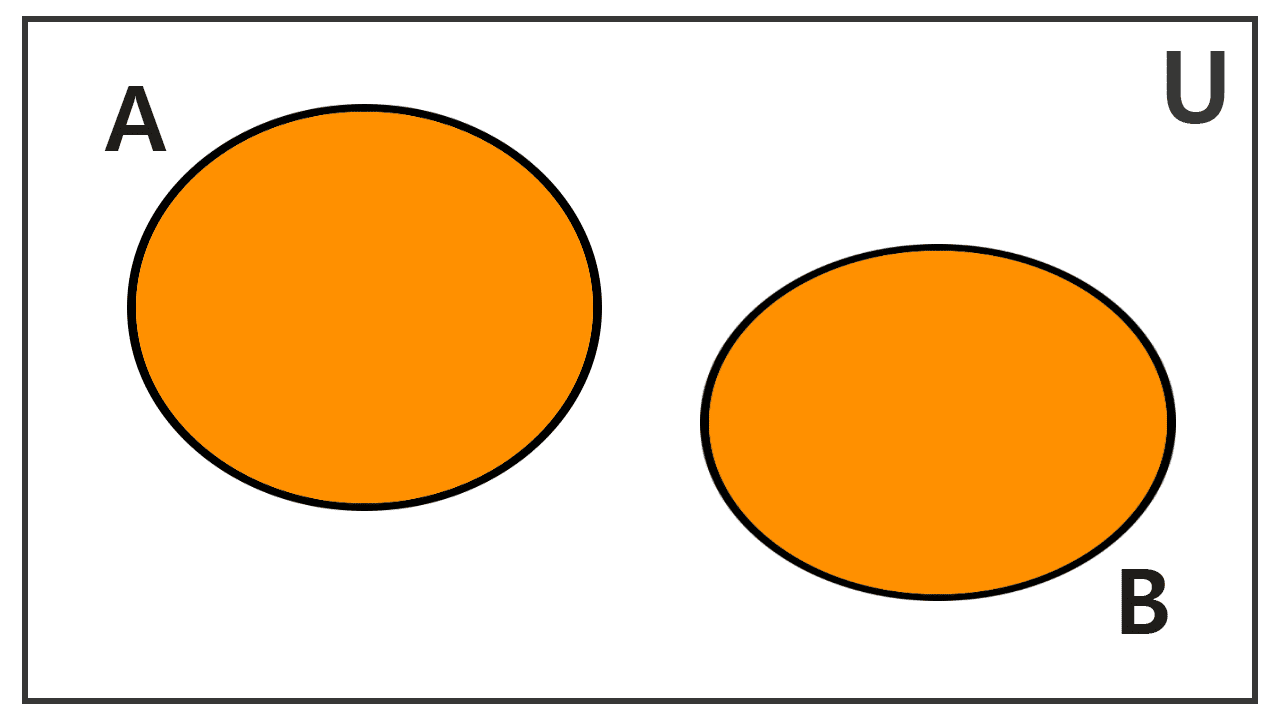
Venn diagrams allow us to visualize this operation. Although sets can be related in different ways, we can illustrate the union by considering three fundamental situations.
The fundamental difference between the union and the intersection of sets lies in the elements each includes: the union of two sets groups all elements belonging to at least one of them; in contrast, the intersection is limited exclusively to the elements shared by the involved sets.
Table of Contents
Examples
Below we will see some examples of the union of sets. It is important to note that if there are repeated elements, they are written only once in the union.
Example 1
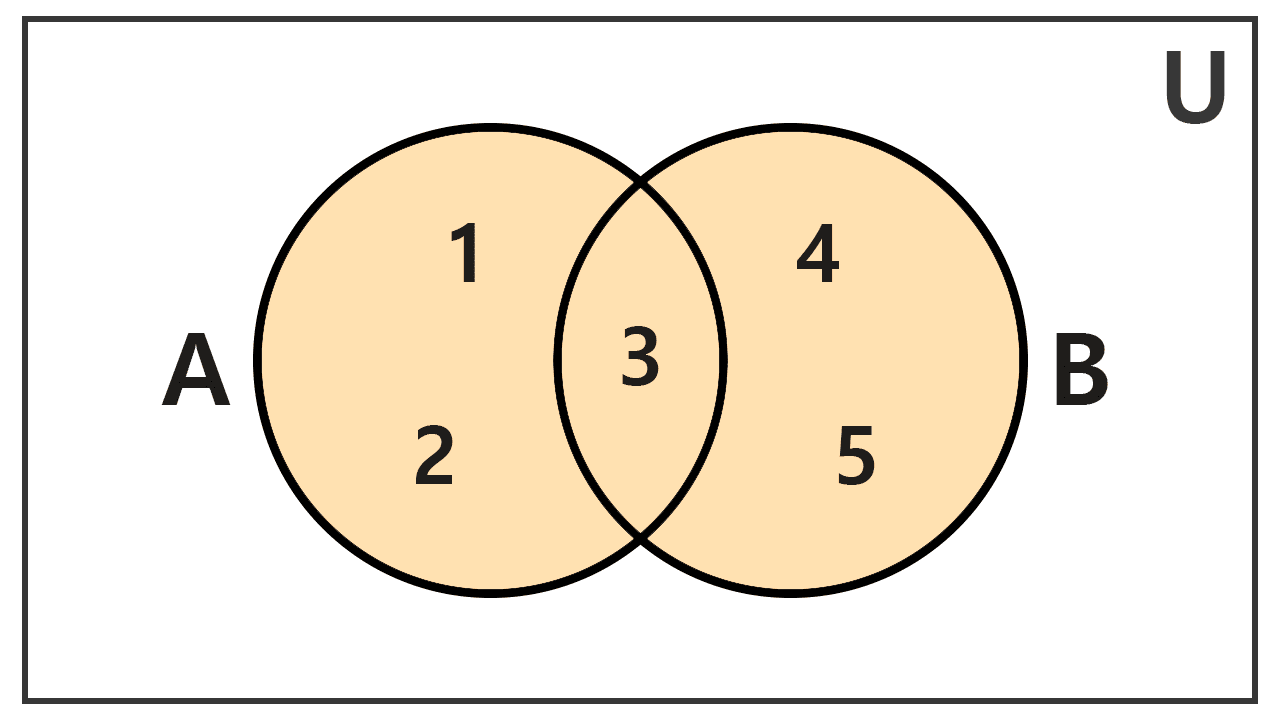
Given A = {1, 2, 3} and B = {3, 4, 5}, calculate their union.
Solution
To find the union of two sets, we combine all the elements that belong to A or B. We observe that the element 3 is present in both sets. However, in the union, repeated elements are included only once. Therefore, by uniting A and B, we get the set:
A ∪ B = {1, 2, 3, 4, 5}
Example 2
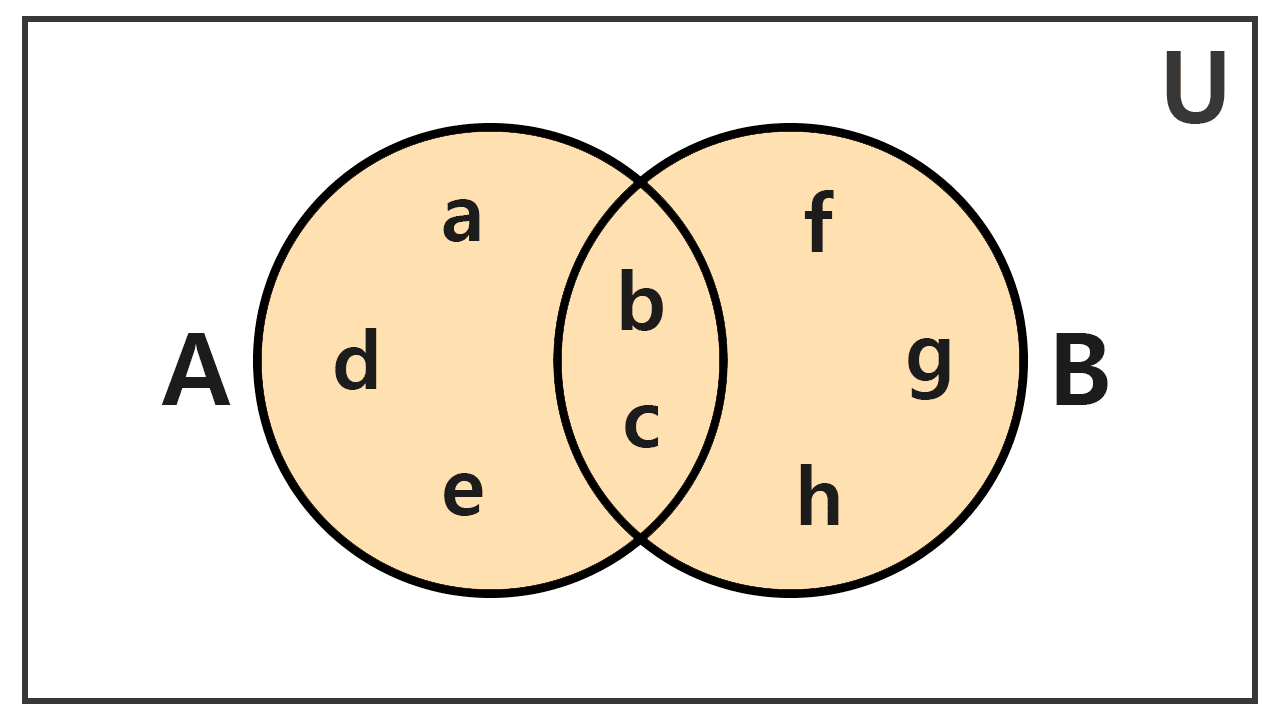
Determine the resulting set from the union of A = {a, b, c, d, e} and B = {b, c, f, g, h}.
Solution
When performing the union of these two sets, we gather all their elements. The elements 'b' and 'c' are common to both, so we only consider them once. The union set is then as follows:
A ∪ B = {a, b, c, d, e, f, g, h}
Example 3
Find the union of sets C = {-1, -2, -3} and D = {1, 2, 3}.
Solution
In this case, sets C and D do not share any elements; they are disjoint sets. The union of two disjoint sets simply groups all the elements of both. Therefore, the union is:
C ∪ D = {-1, -2, -3} ∪ {1, 2, 3} = {-1, -2, -3, 1, 2, 3}
Example 4
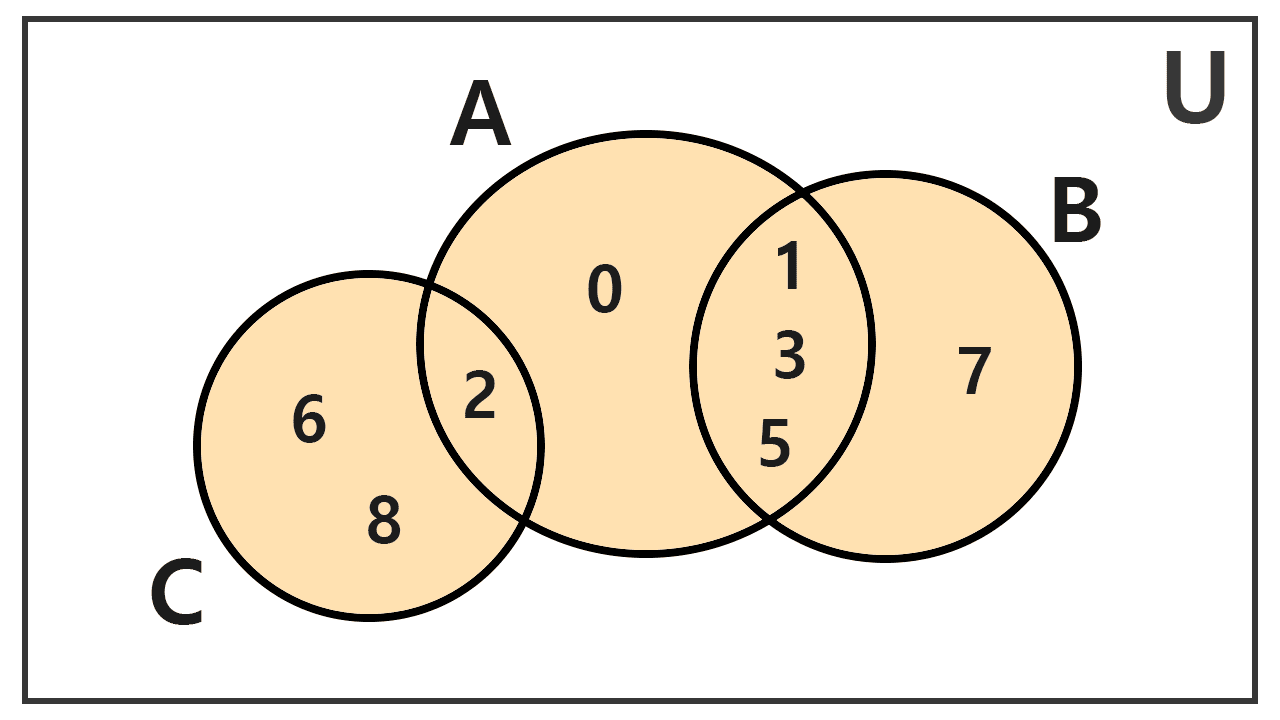
Find the union of sets A, B, and C, where A = {0, 1, 2, 3, 5}, B = {1, 3, 5, 7}, and C = {2, 6, 8}.
Solution
To calculate the union of three sets, we can proceed step by step. First, we unite A and B:
A ∪ B = {0, 1, 2, 3, 5, 7}
Next, we unite this result with set C:
(A ∪ B) ∪ C = {0, 1, 2, 3, 5, 7} ∪ {2, 6, 8}
The element 2 is repeated, but it is counted only once. The final union set is:
A ∪ B ∪ C = (A ∪ B) ∪ C = {0, 1, 2, 3, 5, 6, 7, 8}
Note: The order of the union is arbitrary; we could have first united A with C (or B with C) and the result would be the same. This is due to the associative and commutative properties of this operation.
Example 5
Solve the union of three sets J, K, and L, where J = {1, 2, 3, 4, 5, 6}, K = {1, 3, 5, 7}, and L = {2, 4, 6, 8}.
Solution
We start by uniting J and K:
J ∪ K = {1, 2, 3, 4, 5, 6, 7}
Then, we unite this new set with L:
(J ∪ K) ∪ L = {1, 2, 3, 4, 5, 6, 7} ∪ {2, 4, 6, 8}
The elements 2, 4, and 6 were already present, so the final union of the three sets is:
J ∪ K ∪ L = (J ∪ K) ∪ L = {1, 2, 3, 4, 5, 6, 7, 8}
Example 6
Solve the union of A, B, C, and D, where A = {1, 2}, B = {1}, C = {4, 5}, and D = {-1, 0}.
Solution
We start by uniting A with the singleton set B:
A ∪ B = {1, 2} ∪ {1} = {1, 2}
Then, we unite this result with C:
(A ∪ B) ∪ C = {1, 2} ∪ {4, 5} = {1, 2, 4, 5}
Finally, we unite the previous set with D to get the union of four sets:
((A ∪ B) ∪ C) ∪ D = {1, 2, 4, 5} ∪ {-1, 0}
Since there are no repeated elements between these sets, the final result is the grouping of all elements:
A ∪ B ∪ C ∪ D = {-1, 0, 1, 2, 4, 5}
Example 7
Find the union of the sets S = {x ∈ N | x < 10} and T = {x ∈ N | 2x ≤ 20}.
Solution
The sets are given in set-builder notation; it is useful to express both in roster form to visualize their elements. Set S consists of the natural numbers less than 10:
S = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Set T includes the natural numbers for which 2x ≤ 20, meaning x ≤ 10, so T = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. We see that T has one more element than S, which is “10”. The union results in:
S ∪ T = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Example 8
Let P be the set of even natural numbers and I be the set of odd natural numbers. Find P ∪ I.
Solution
Set P contains all even numbers: P = {2, 4, 6, …}; and set I contains all odd numbers: I = {1, 3, 5, 7, …}. There is no natural number that is both even and odd, so they are disjoint sets. Their union therefore includes each and every natural number. Thus, P ∪ I is equal to the set of natural numbers, N.
Properties
The union operation in set theory follows a series of fundamental properties that help us simplify its calculation. We will look at the most important ones below.
1) Commutative property: The order in which the sets are united does not alter the result.
A ∪ B = B ∪ A
2) Associative property: The way sets are grouped to perform the union does not affect the final result.
(A ∪ B) ∪ C = A ∪ (B ∪ C)
3) Idempotence: The union of a set with itself is the set itself.
A ∪ A = A
4) Identity property (or neutral element): The union of any set with the empty set is the original set.
A ∪ ∅ = A
5) Domination property: The union of any set with the universal set is the universal set.
A ∪ U = U
6) Distributivity with respect to intersection: The union of a set with the intersection of two other sets is equal to the intersection of the unions of the first set with each of the other two.
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
7) De Morgan's Law: The complement of the union of sets is equal to the intersection of their complements.
(A ∪ B)’ = A’ ∩ B’
8) Cardinality: The number of elements in the union of two finite sets is the sum of their elements minus the number of elements they share (their intersection).
|A ∪ B| = |A| + |B| - |A ∩ B|
9) Properties related to subsets:
- If two sets are a subset of a third set, their union is also a subset of it: if A ⊆ C and B ⊆ C, then A ∪ B ⊆ C.
- If one set is a subset of another, their union is equal to the larger set: if A ⊆ B, then A ∪ B = B.
- If a set is included in two sets at the same time, then it is also included in their union: if X ⊆ A and X ⊆ B, then X ⊆ A ∪ B.
Leave a Reply

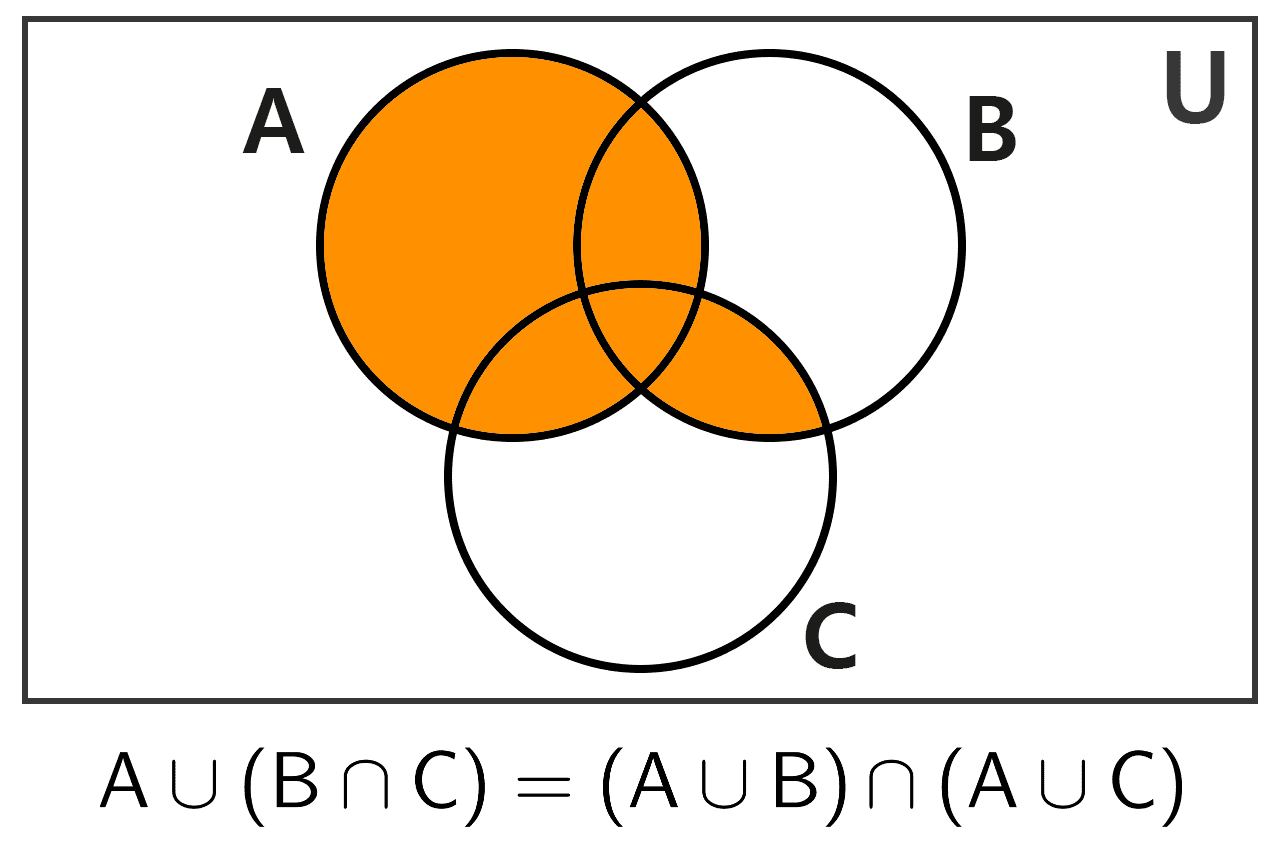

Related posts