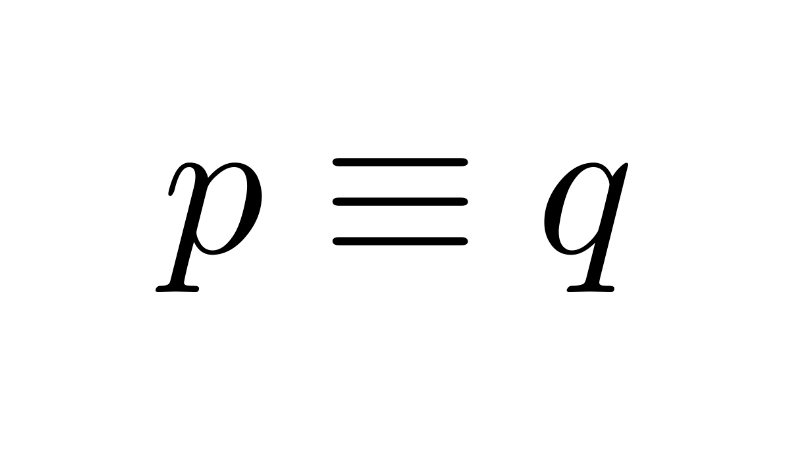
Contingency in Propositional Logic
In propositional logic, a contingency is a compound proposition that is true in some cases and false in others, and therefore is neither a tautology nor a contradiction.
Contingent propositions are the most common in natural language, as they are the ones we use to describe the real world and make statements about what happens in it. Some examples of contingent propositions in everyday language are:
- “It is cold and it is raining”, is only true when it is true that it is cold and raining at the same time. If it is only cold but not raining, or vice versa, the proposition is false; it is also false if it is neither cold nor raining.
- “John is eating bread or watching television”, is a true proposition when the first and second statements are true, or when at least one of them is true; the proposition is false when both statements are false.
Examples
To know if a proposition is a contingency, we can construct its truth table: if there is at least one true value and one false value, it is a contingency. If all values are true, it is a tautology; if all are false, it is a contradiction.
Example 1
The proposition ¬p ∧ q ↔ q ∨ ¬q is a two-variable contingency, its truth table is:
| p | q | ¬p | ¬q | ¬p ∧ q | q ∨ ¬q | ¬p ∧ q ↔ q ∨ ¬q |
|---|---|---|---|---|---|---|
| T | T | F | F | F | T | F |
| T | F | F | T | F | T | F |
| F | T | T | F | T | T | T |
| F | F | T | T | F | T | F |
Note that the proposition is only true when p is false and q is true, and is false in all other cases.
Example 2
The compound proposition ¬p ∨ q is a contingency:
| p | q | ¬p | ¬p ∨ q |
|---|---|---|---|
| T | T | F | T |
| T | F | F | F |
| F | T | T | T |
| F | F | T | T |
Example 3
¬p ∧ q → r is a three-variable contingent proposition:
| p | q | r | ¬p | ¬p ∧ q | ¬p ∧ q → r |
|---|---|---|---|---|---|
| T | T | T | F | F | T |
| T | T | F | F | F | T |
| T | F | T | F | F | T |
| T | F | F | F | F | T |
| F | T | T | T | T | T |
| F | T | F | T | T | F |
| F | F | T | T | F | T |
| F | F | F | T | F | T |
The only case where the proposition is false is when p is false, q is true, and r is false.
Other examples
- ¬p
- p ∧ q
- p ∨ q
- p → q
- p ↔ q
It can be verified that these propositions are contingent by looking at the truth tables of the logical connectives.
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Logical Quantifiers
Propositional Function
Logical Laws
Logical Connectives in Mathematics
Logical Tautology
Leave a Reply
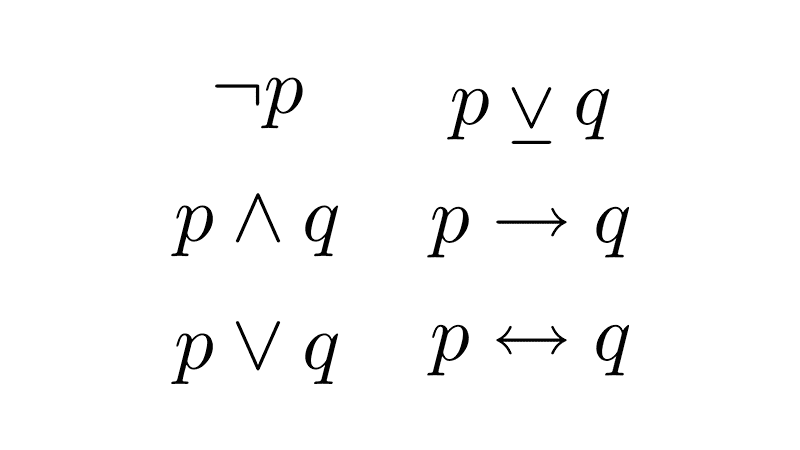
Related posts