Logical Negation
Negation is a logical connective that takes a proposition and converts it into its logical opposite. If a proposition is true, its negation is false, and vice versa. It is denoted by the symbol ¬, therefore, the negation of the proposition p is ¬p.
Examples of negation:
- If p is the proposition "it is raining," then ¬p is "it is not raining."
- If q is "the number 7 is even," then ¬q is "the number 7 is not even."
- If r is “the Sun is bright,” the proposition ¬r is “it is false that the Sun is bright.”
Table of Contents
Truth Table
The truth table for negation returns a false value when the original proposition is true and a true value when the original proposition is false.
| p | ¬p |
|---|---|
| T | F |
| F | T |
Examples
The following table shows examples of propositions in the first column and their negations in the second.
| Original Proposition | Negation |
|---|---|
| John finished his homework | John did not finish his homework |
| 2+2=5 | 2+2≠5 |
| The sky is not blue | The sky is blue |
| Mary is an engineer | Mary is not an engineer |
| Roses are plants | Roses are not plants |
| It is raining and it is cold | It is not true that it is raining and it is cold |
| Charles is at home or at the office | It is false that Charles is at home or at the office |
It is possible to negate both a simple proposition (the first five examples) and a compound proposition (the last two examples). In the case of compound propositions, the negation can be more complex and will depend on the type of logical connective that joins the simple propositions composing it.
There are specific rules for negating compound propositions involving conjunctions, disjunctions, conditionals, and biconditionals. Also, the negation of a negation (as in the example "the sky is not blue") has a particular rule. We will look at all of them below.
Properties of Negation
The logical connective of negation has the properties we will see below.
Double Negation
Also called the law of involution, it states that the negation of the negation of a proposition returns the original proposition. In symbols, this is expressed as:
¬(¬p) ≡ p
Examples
- "It is not true that the book is not on the table" is equivalent to saying "the book is on the table."
- "It is false that Peter failed the exam" is equivalent to "Peter passed the exam."
- "It is not true that Mary does not live in Buenos Aires" is equivalent to "Mary lives in Buenos Aires."
De Morgan's Laws
Negation is not distributive; however, De Morgan's laws allow for a kind of "distributivity" of negation over a conjunction and a disjunction.
Negation of a conjunction: it is obtained by negating each of the simple propositions that compose it and joining them with a disjunction.
¬(p ∧ q) ≡ ¬p ∨ ¬q
Examples
- For the compound proposition "it is raining and it is cold," the negation is "it is not raining or it is not cold."
- The proposition "Ann goes to the movies and has dinner with friends" has the negation "Ann does not go to the movies or does not have dinner with friends."
- The proposition "Peter studies hard and gets good grades" is negated as "Peter does not study hard or does not get good grades."
Negation of a disjunction: it is obtained by negating each of the simple propositions that compose it and joining them with a conjunction.
¬(p ∨ q) ≡ ¬p ∧ ¬q
Examples
- If the compound proposition is "Charles is at his house or at his office," its negation is "Charles is not at his house and is not at his office."
- The proposition "tomorrow I will go to the park or the museum" has the negation "tomorrow I will not go to the park and I will not go to the museum."
- The proposition "John eats pasta or pizza" is negated as "John does not eat pasta and does not eat pizza."
Negation of Conditional and Biconditional
Negation of a conditional: negating an implication p → q is equivalent to the conjunction of the antecedent and the negation of the consequent. In symbols:
¬(p → q) ≡ p ∧ ¬q
Example: the proposition "if it is raining (p), then I carry an umbrella (q)" has as its negation "it is not true that if it is raining I carry an umbrella," which is equivalent to saying "it is raining and I am not carrying an umbrella."
Negation of a biconditional: the negation of a double implication is equivalent to the exclusive disjunction of the component propositions. In symbols:
¬(p ↔ q) ≡ p ⊻ q
Example: for the proposition "it rains if and only if it is cold," its negation is "either it rains or it is cold, but not both."
Other Properties
- It is not possible for a proposition and its negation to be true at the same time. This is known as the principle of non-contradiction: ¬(p ∧ ¬p).
- The proposition p ∨ ¬p is always true and is known as the law of the excluded middle: a proposition is either true or false, with no intermediate option.
- The negation of a tautology (a proposition that is always true) is a contradiction (a proposition that is always false), and the negation of a contradiction is a tautology.
Negation in Set Theory
In set theory, logical negation is used to define the complement: the complement of a set A, denoted by A' or Ac, is the set of all elements that belong to the universal set but do not belong to A.
A' = {x ∈ U | x ∉ A}
Note that the expression x ∉ A is equivalent to saying ¬(x ∈ A).
Examples
- If we take the set of all people as the universal set and set A as people over 18 years old, the complement of A consists of all people who are not over 18.
- Consider the universal set U = {1, 2, 3, 4, 5} and the set A = {2, 4}. Then, the complement of A is A' = {1, 3, 5}, because it is composed of all the elements that A is missing to be equal to the universal set.
The complement of a set has a series of properties that are closely related to the properties of negation we saw earlier. Among them are:
- Involution property: the complement of the complement of a set is equal to the original set: (A')' = A.
- De Morgan's law for union: the complement of the union of two sets is equal to the intersection of their complements: (A ∪ B)' = A' ∩ B'.
- De Morgan's law for intersection: the complement of the intersection of two sets is equal to the union of their complements: (A ∩ B)' = A' ∪ B'.
Recall that, in set theory, the intersection (∩) is equivalent to the conjunction (∧), and the union (∪) is equivalent to the disjunction (∨).
Negation in Logic Circuits
In the field of digital logic and electronics, the logic circuit for negation, also known as an inverter or NOT gate, is a fundamental electronic circuit that performs the logical negation operation on an input signal. Its main function is to invert the truth value of the input signal, meaning if the input is 1 (high level), the output will be 0 (low level), and vice versa.
| A (input) | ¬A (output) |
|---|---|
| 1 | 0 |
| 0 | 1 |
Negation in Computer Science
The logical connective of negation is known as the NOT operator in computer science and plays a crucial role in building algorithms and manipulating data. Its main function is to invert the truth value of a Boolean expression.
Logical negation is represented in most programming languages as ! (exclamation mark) or not (keyword). This operator is applied before the Boolean expression to be negated.
Logical negation can be combined with other logical operators to form more complex expressions. For example:
- Negated conjunction: not (P and Q) is equivalent to not P or not Q.
- Negated disjunction: not (P or Q) is equivalent to not P and not Q.
Note that the operator's behavior is governed by De Morgan's Laws.
Logical negation, along with other operations, is fundamental to the design and operation of modern processors. It is applied in the ALU (Arithmetic Logic Unit), which is responsible for performing arithmetic operations such as addition, subtraction, multiplication, and division. It is also used in other internal components for conditional decisions and flow control in programs and operating systems.
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply


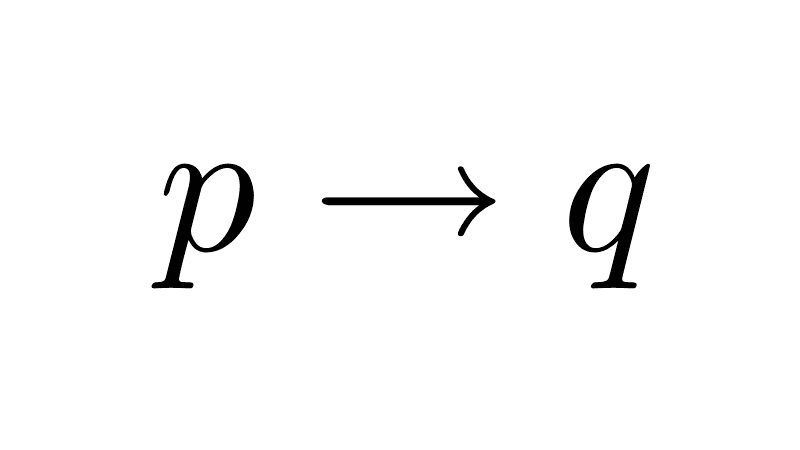
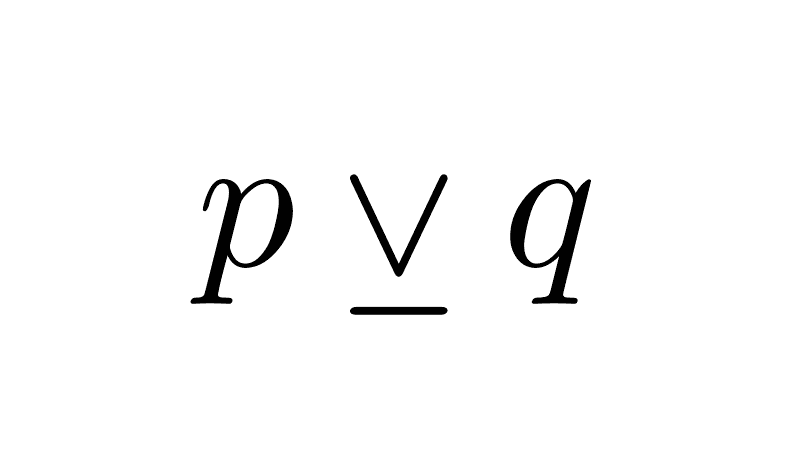
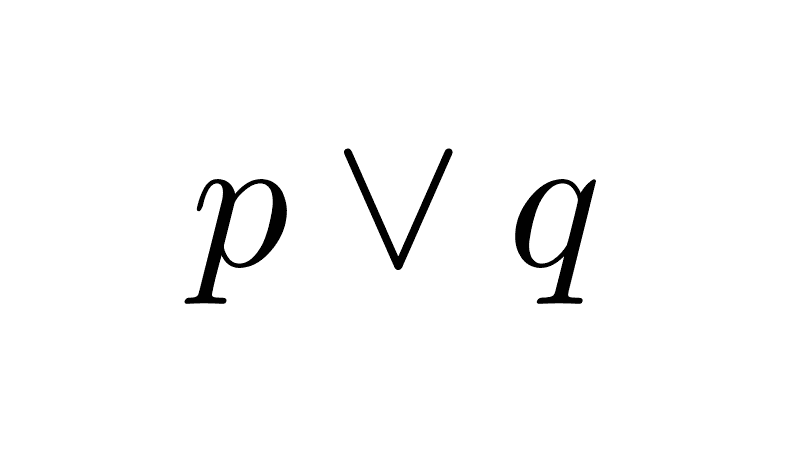

Related posts