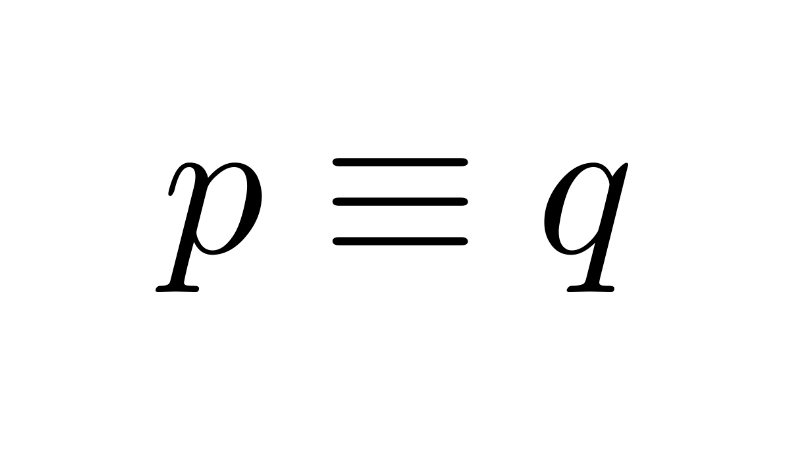
Truth Tables
Truth tables are tools that allow us to determine the truth values of compound propositions by considering all possible interpretations of the simple propositions that form them. In other words, they help us determine whether a compound proposition is true or false, depending on the truth values of its constituent simple propositions.
Table of Contents
Truth Tables of Logical Connectives
Simple propositions are those that cannot be broken down into others, while compound propositions are formed from simple propositions using logical connectives (not, and, or, if... then, if and only if).
Each connective has its own truth table. The true value is indicated by the letter T (for true) or the number 1; the false value is indicated by the letter F or the number 0. We will now see how each connective behaves.
Negation (not)
The negation of a proposition p, symbolized as ¬p and read as "not p," is false if the original proposition is true, and true if the original is false.
| p | ¬p |
|---|---|
| T | F |
| F | T |
Example
p: "It is raining"
¬p: "It is not raining"
Conjunction (and, &)
The conjunction of two propositions p and q, symbolized as p ∧ q and read as "p and q," is true only if both propositions are true; it is false in all other cases.
| p | q | p ∧ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Example
p: "It is sunny"
q: "It is hot"
p ∧ q: "It is sunny and it is hot"
Disjunction (or)
The disjunction of two propositions p and q, symbolized as p ∨ q and read as "p or q," is false only if both propositions are false; it is true in all other cases.
| p | q | p ∨ q |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Example
p: "I will buy tomatoes"
q: "I will buy lettuce"
p ∨ q: "I will buy tomatoes or lettuce, or both"
Exclusive Disjunction (either... or, but not both; XOR)
The exclusive disjunction of two propositions p and q, symbolized as p ⊻ q and read as "either p or q, but not both," is true only when one of the propositions is true and the other is false; it is false when both have the same truth value.
| p | q | p ⊻ q |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
Example
p: "It is sunny"
q: "It is cloudy"
p ⊻ q: "Either it is sunny or it is cloudy, but not both"
Conditional or Implication (if... then...)
The conditional of two propositions p and q, symbolized as p → q and read as "if p, then q," is false only when the first proposition (the antecedent) is true and the second (the consequent) is false; it is true in all other cases.
| p | q | p → q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Example
p: "It is raining"
q: "The sky is cloudy"
p → q: "If it is raining, then the sky is cloudy"
Biconditional or Double Implication (if and only if)
The biconditional of two propositions p and q, symbolized as p ↔ q and read as "p if and only if q," is true only when both propositions are true or both are false; it is false when they have different truth values.
| p | q | p ↔ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
Example
p: "It is raining"
q: "The sky is cloudy"
p ↔ q: "It is raining if and only if the sky is cloudy"
How to Make Truth Tables
Next, we will look at step-by-step examples of how to construct truth tables. Since the table will have one row for each possible interpretation, the total number of rows will be 2n plus the header row, where n is the number of simple propositions or variables.
Tables with Two Variables
When there are two simple propositions, the truth table will have 22 = 4 rows plus the header.
Example 1: (p ∧ q) → p
First, we interpret the compound proposition as an implication with the proposition "p ∧ q" as the antecedent and "p" as the consequent. We place each simple proposition in a column and write the possible combinations of truth values in each row (TT, TF, FT, FF).
| p | q | ... |
|---|---|---|
| T | T | ... |
| T | F | ... |
| F | T | ... |
| F | F | ... |
We add a third column with the antecedent of the implication: the conjunction p ∧ q. Referring to the connectives' truth tables, we know that this conjunction is true only when both p and q are true, and false in all other cases. With this information, we complete the column:
| p | q | p ∧ q | ... |
|---|---|---|---|
| T | T | T | ... |
| T | F | F | ... |
| F | T | F | ... |
| F | F | F | ... |
Now we add the fourth and final column, which will contain the complete proposition (p ∧ q) → p that we want to evaluate. To determine its truth values, we must look only at the values in the p ∧ q column and the p column, highlighted in yellow. They are connected by an implication, which is false only if the antecedent (p ∧ q) is true and the consequent (p) is false. There are no rows where this occurs, so the proposition (p ∧ q) → p is true in all cases.
| p | q | p ∧ q | (p ∧ q) → p |
|---|---|---|---|
| T | T | T | T |
| T | F | F | T |
| F | T | F | T |
| F | F | F | T |
With this, we have solved the truth table, which looks like this without the colors:
| p | q | p ∧ q | (p ∧ q) → p |
|---|---|---|---|
| T | T | T | T |
| T | F | F | T |
| F | T | F | T |
| F | F | F | T |
The step-by-step process for creating a truth table is summarized in the box below.
Steps to Create a Truth Table
- Calculate the number of rows the truth table will have. This is equal to 2n plus the header row, where n is the number of simple propositions.
- Calculate the number of columns the table will have. This is equal to the number of simple propositions plus the number of logical connectives in the expression, counting each occurrence.
- Break down the compound proposition in the header, considering the hierarchy of connectives. The first columns will contain the simple propositions, and the last column will contain the original proposition.
- Write all possible interpretations (combinations of truth values) for the simple propositions in the rows. For example, with two propositions, there are four possible interpretations.
- Complete the rest of the table using the truth tables for the logical connectives. The final column, for the original proposition we are analyzing, will show its truth value for each interpretation.
If you want to check your results, you can use this tool:
Example 2: (¬p ∧ q) ↔ (q ∨ ¬q)
First, we identify that there are two simple propositions, so the table will have four rows. The first two columns will be for p and q, followed by columns for ¬p, ¬q, ¬p ∧ q, q ∨ ¬q, and finally, the complete proposition (¬p ∧ q) ↔ (q ∨ ¬q).
Let's start with the first four columns. Since we are dealing with negation, the truth value will be the opposite of the original proposition. For example, in the third row, p is F, so ¬p will be T; likewise, q is T, so ¬q will be false.
| p | q | ¬p | ¬q | ... |
|---|---|---|---|---|
| T | T | F | F | ... |
| T | F | F | T | ... |
| F | T | T | F | ... |
| F | F | T | T | ... |
Now we add the columns for the conjunction and the disjunction:
| p | q | ¬p | ¬q | ¬p ∧ q | q ∨ ¬q | ... |
|---|---|---|---|---|---|---|
| T | T | F | F | F | T | ... |
| T | F | F | T | F | T | ... |
| F | T | T | F | T | T | ... |
| F | F | T | T | F | T | ... |
Finally, we add the original proposition. Since it's a biconditional, it will be true only when its component propositions have the same truth value. We need to look at the columns highlighted in yellow. In the third row, the propositions have the same truth value (both are T), so the biconditional will be true there, and false in the other cases.
| p | q | ¬p | ¬q | ¬p ∧ q | q ∨ ¬q | (¬p ∧ q) ↔ (q ∨ ¬q) |
|---|---|---|---|---|---|---|
| T | T | F | F | F | T | F |
| T | F | F | T | F | T | F |
| F | T | T | F | T | T | T |
| F | F | T | T | F | T | F |
With this, we have solved the truth table, which looks like this:
| p | q | ¬p | ¬q | ¬p ∧ q | q ∨ ¬q | (¬p ∧ q) ↔ (q ∨ ¬q) |
|---|---|---|---|---|---|---|
| T | T | F | F | F | T | F |
| T | F | F | T | F | T | F |
| F | T | T | F | T | T | T |
| F | F | T | T | F | T | F |
Example 3: ¬(p ∧ q → p)
We construct the table similarly to the previous cases, and it should look like this:
| p | q | p ∧ q | p ∧ q → p | ¬(p ∧ q → p) |
|---|---|---|---|---|
| T | T | T | T | F |
| T | F | F | T | F |
| F | T | F | T | F |
| F | F | F | T | F |
In Example 1, the proposition was true for every interpretation; in Example 2, it is sometimes true and sometimes false; and in Example 3, the values are always false. Each case has a special name in propositional logic.
- If a compound proposition is true for all interpretations, it is called a tautology or a logical law, as in Example 1.
- If a compound proposition is true for some interpretations and false for others, it is called a contingency, as in Example 2.
- If a compound proposition is false for all interpretations, it is called a contradiction, as in Example 3.
Example 4: (p → q) ↔ (¬q→¬p)
We create the table for this proposition in the same way as before and arrive at:
| p | q | ¬p | ¬q | p → q | ¬q → ¬p | (p → q) ↔ (¬q → ¬p) |
|---|---|---|---|---|---|---|
| T | T | F | F | T | T | T |
| T | F | F | T | F | F | T |
| F | T | T | F | T | T | T |
| F | F | T | T | T | T | T |
We have found a tautology. Specifically, this tells us that an implication is equivalent to its contrapositive.
Example 5: (p → q) ∧ (q → p)
| p | q | p → q | q → p | (p → q) ∧ (q → p) |
|---|---|---|---|---|
| T | T | T | T | T |
| T | F | F | T | F |
| F | T | T | F | F |
| F | F | T | T | T |
This time, the table results in a contingency. Note that the proposition is true when the simple propositions are both true or both false. This behavior is the same as that of the biconditional; in fact, a logical law states that the proposition (p → q) ∧ (q → p) is equivalent to p ↔ q.
Example 6: (p → q) ∨ (q → p)
| p | q | p → q | q → p | (p → q) ∨ (q → p) |
|---|---|---|---|---|
| T | T | T | T | T |
| T | F | F | T | T |
| F | T | T | F | T |
| F | F | T | T | T |
The table shows that the proposition (p → q) v (q → p) is a tautology.
Tables with Three Variables
When we have three propositions, the truth table can be constructed using the same procedure as before, just keeping in mind that the number of rows will be 23=8 plus the header.
Example 1: (¬p ∧ q) → r
Pay close attention to how the true and false values are distributed in the first three columns. The table should look like this:
| p | q | r | ¬p | ¬p ∧ q | (¬p ∧ q ) → r |
|---|---|---|---|---|---|
| T | T | T | F | F | T |
| T | T | F | F | F | T |
| T | F | T | F | T | T |
| T | F | F | F | F | T |
| F | T | T | T | T | T |
| F | T | F | T | T | F |
| F | F | T | T | F | T |
| F | F | F | T | F | T |
In this case, because the final column has both true and false values, we are dealing with a contingency.
Example 2: [(p ∧ q) ∧ r] → p
| p | q | r | p ∧ q | (p ∧ q) ∧ r | [(p ∧ q) ∧ r] → p |
|---|---|---|---|---|---|
| T | T | T | T | T | T |
| T | T | F | T | F | T |
| T | F | T | F | F | T |
| T | F | F | F | F | T |
| F | T | T | F | F | T |
| F | T | F | F | F | T |
| F | F | T | F | F | T |
| F | F | F | F | F | T |
Looking at the last column, we can see that this is a tautology.
Example 3: (p ∧ q) ∧ (r ∧¬p)
| p | q | r | ¬p | p ∧ q | r ∧¬p | (p ∧ q) ∧ (r ∧ ¬p) |
|---|---|---|---|---|---|---|
| T | T | T | F | T | F | F |
| T | T | F | F | T | F | F |
| T | F | T | F | F | F | F |
| T | F | F | F | F | F | F |
| F | T | T | T | F | T | F |
| F | T | F | T | F | F | F |
| F | F | T | T | F | T | F |
| F | F | F | T | F | F | F |
Since we have only false values for every interpretation, the proposition results in a contradiction.
Example 4: (p ∧ q) → r
| p | q | r | p ∧ q | (p ∧ q) → r |
|---|---|---|---|---|
| T | T | T | T | T |
| T | T | F | T | F |
| T | F | T | F | T |
| T | F | F | F | T |
| F | T | T | F | T |
| F | T | F | F | T |
| F | F | T | F | T |
| F | F | F | F | T |
The proposition (p ∧ q) → r is a contingency.
Example 5: (p ∨ q) → r
| p | q | r | p ∨ q | (p ∨ q) → r |
|---|---|---|---|---|
| T | T | T | T | T |
| T | T | F | T | F |
| T | F | T | T | T |
| T | F | F | T | F |
| F | T | T | T | T |
| F | T | F | T | F |
| F | F | T | F | T |
| F | F | F | F | T |
The truth table shows that the proposition is a contingency.
Example 6: (p → q) ∧ (q → r) → (p → r)
| p | q | r | p → q | q → r | p → r | (p → q) ∧ (q → r) | [(p → q) ∧ (q → r)] → (p → r) |
|---|---|---|---|---|---|---|---|
| T | T | T | T | T | T | T | T |
| T | T | F | T | F | F | F | T |
| T | F | T | F | T | T | F | T |
| T | F | F | F | T | F | F | T |
| F | T | T | T | T | T | T | T |
| F | T | F | T | F | T | F | T |
| F | F | T | T | T | T | T | T |
| F | F | F | T | T | T | T | T |
The proposition [(p → q) ∧ (q → r)] → (p → r) turns out to be a tautology. In fact, this is a rule of inference known as transitivity or hypothetical syllogism.
Tables with Four or More Variables
Logical truth tables with more than three propositional variables can be constructed, but they are impractical. For example, to build a table with four simple propositions, you would need 24=16 rows plus the header. With five propositions, 25=32 rows plus the header are required. The number of rows increases exponentially, but we can easily manage with three or fewer propositions.
Example: (p ∧ q) ∨ (r ∧ s)
| p | q | r | s | p ∧ q | r ∧ s | (p ∧ q) ∨ (r ∧ s) |
|---|---|---|---|---|---|---|
| T | T | T | T | T | T | T |
| T | T | T | F | T | F | T |
| T | T | F | T | T | F | T |
| T | T | F | F | T | F | T |
| T | F | T | T | F | T | T |
| T | F | T | F | F | F | F |
| T | F | F | T | F | F | F |
| T | F | F | F | F | F | F |
| F | T | T | T | F | T | T |
| F | T | T | F | F | F | F |
| F | T | F | T | F | F | F |
| F | T | F | F | F | F | F |
| F | F | T | T | F | T | T |
| F | F | T | F | F | F | F |
| F | F | F | T | F | F | F |
| F | F | F | F | F | F | F |
We can see that this is a contingency.
History
Truth tables emerged from a long process of development in formal logic. While their systematic structure was popularized in the 20th century, their roots trace back to earlier works. The philosopher and scientist Charles Sanders Peirce, in the 1880s, made key contributions by exploring methods to analyze propositions through combinations of truth values.
The consolidation of these tables as a system is mainly attributed to Ludwig Wittgenstein, who used them in his Tractatus Logico-Philosophicus (1921) to examine all possible combinations of truth values in propositions. Simultaneously, the mathematician Emil Post developed an equivalent approach in his doctoral thesis (1920), linking logic to primitive computation.
These advances were built on earlier foundations, such as George Boole's algebra (mid-19th century), which translated logical operations into equations. Truth tables, with their visual clarity, gained practical relevance with the rise of electronics and computing in the 20th century, becoming crucial for designing logic circuits and algorithms. Today, they remain a cornerstone in logic, philosophy, and computer science.
Additional Resources
If you're practicing, you can check your truth tables using an online truth table generator:
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

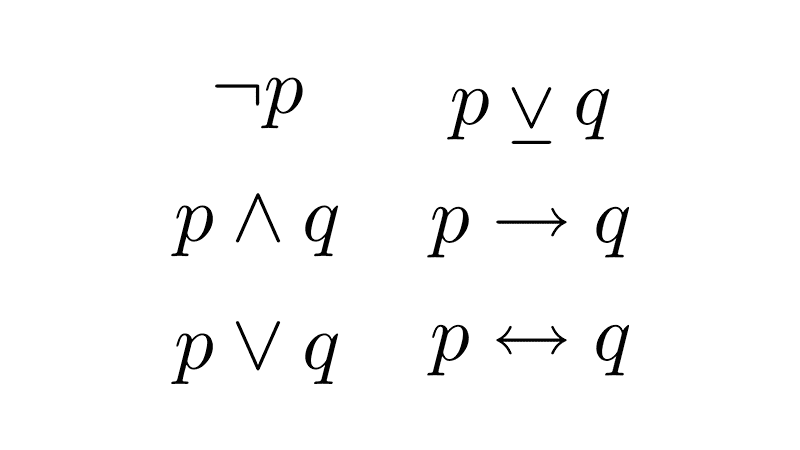
Related posts