Singleton Set
A singleton set is one that contains exactly one element. This element can be any object, number, symbol, or entity defined within the context of the set.
Table of Contents
Examples
Below are some examples of singleton sets given by roster and by set-builder notation.
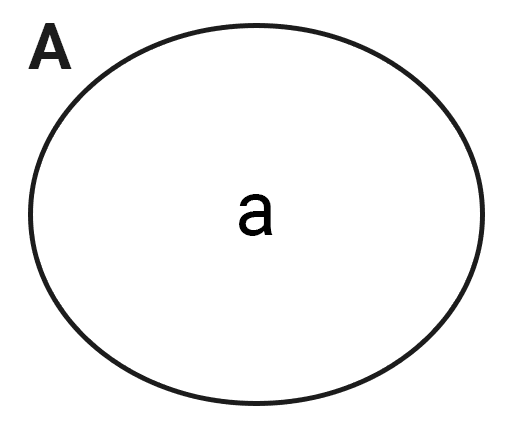
- The set A = {a} is a singleton set as it contains only one element: "a".
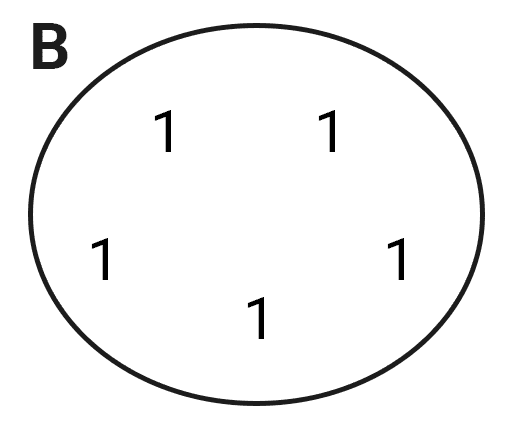
- The set B = {1, 1, 1, 1, 1} is a singleton set because it has only one object, regardless of how many times it is written.
- The set C = {x | x is the initial letter of the word "casa"} is a singleton set. Given by roster, it is C = {c}.
- The set of solutions for the linear equation 2x + 1 = 3 is a singleton set, as { x | 2x+1=3 } = {1}.
- The power set of the empty set is a singleton set, as it has only one element, the empty set itself: P(Ø) = {Ø}.
- The set M = { x | x is an integer and 2 < x < 4 } is a singleton set, as we can deduce that M = {3}.
- The set T = { x | x is the planet inhabited by humans } is a singleton set, as T = {Earth}.
- The set R = { {1, 2, 3} } is a singleton set, as its only element is the set {1, 2, 3}.
- The set L = { x | x is a natural satellite of Earth } is a singleton set, as the set can be expressed as L = {Moon}.
- The intersection of the sets P = {5, 7, 9} and Q = {0, 1, 9} is P ∩ Q = {9}, a singleton set.
Properties
Singleton sets have the following properties.
- A singleton set has only two subsets: itself and the empty set. Its power set is composed of these same two sets.
- The cardinality of a singleton set is one, meaning if A is a singleton set, then |A| = 1.
- The intersection of a singleton set with any other set will either consist of the same element or be the empty set, depending on whether they share that element.
- The intersection between two singleton sets is either the set itself or the empty set, depending on whether the singleton sets are equal or not.
- The complement of a singleton set in a universal set is the set containing all elements that are in the universal set but not in the singleton set.
Practice Exercises
Exercise 1: If the set *A=\{2,a,b\}* is a singleton set, calculate *a+b.*
Solution:
Since A is a singleton set, all its elements are equal, meaning *2=a=b.* From this, we deduce that *a=2* and *b=2,* therefore *a+b=2+2=4.*
Exercise 2: The sets *A=\{2m, 12, n+2\}* and *B=\{20, 5p, q\}* are singleton sets. Calculate the sum *m+n+p+q.*
Solution:
Since A and B are singleton sets, both have only one element, meaning:
For A: *2m=12=n+2*
We can find *m* and *n* by simultaneously solving the equations *2m=12* and *n+2=12.* From these, we deduce that *m=6* and *n=10.*
For B: *20=5p=q*
We can find *p* and *q* by solving the equations *20=5p* and *20=q.* From these, we deduce that *p=4* and *q=20.*
With the required values, we can calculate *m+n+p+q=6+10+4+20=40*
Exercise 3: The set *A=\{a+b; b+c; a+c; 6\}* is a singleton set. Calculate *a+b+c.*
Solution:
Since A is a singleton set, all its elements are equal, meaning: *a+b=b+c=a+c=6,* as a system of equations:
*\begin{cases} a+b=6 \\ b+c=6 \\ a+c=6 \end{cases}*
Solving the system reveals that *a=3,* *b=3,* and *c=3,* therefore *a+b+c=9.*
Exercise 4: Given the singleton sets: *A=\{x+7; 2x+5\}* and *B=\{y-3; 5y-15\},* what is the value of *x+y*?
Solution:
Since A is a singleton set, *x+7=2x+5,* from which we find *x=2.* Since B is also a singleton set, it must be that *y-3=5y-15,* from which we find *y=3.* Having *x* and *y,* we can calculate *x+y=2+3=5.*
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

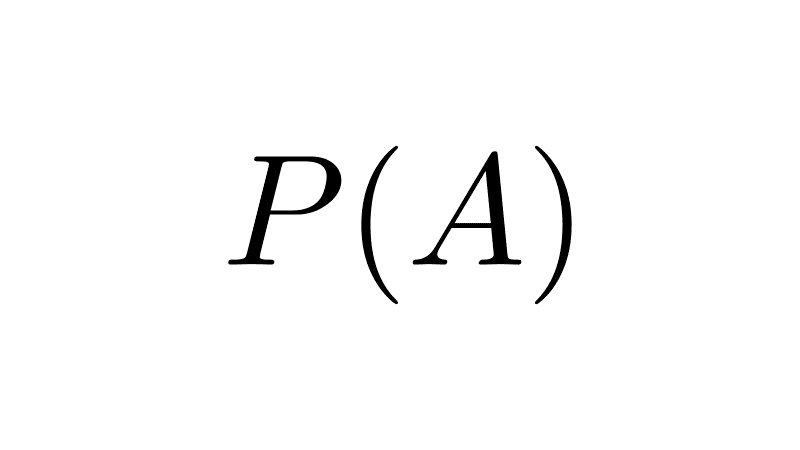
Related posts