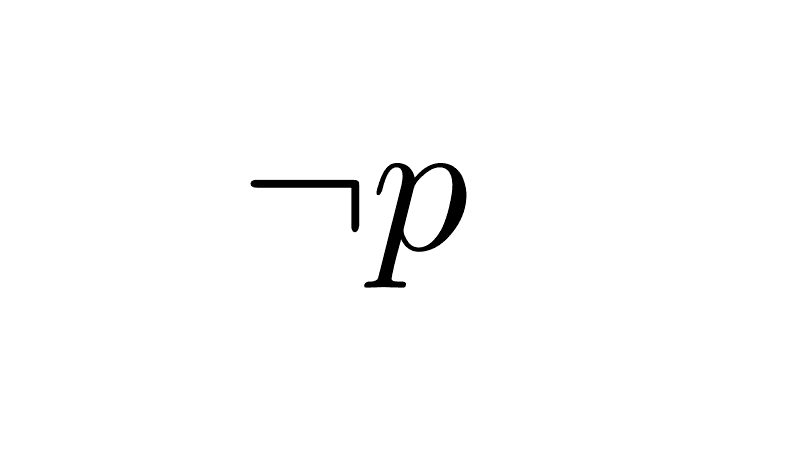
Logical Connectives in Mathematics
Logical connectives (also called connectors or operators) are symbols or words that allow for the formation of new propositions from existing ones. In propositional logic, their function is to join two or more propositions (simple or compound) to create a compound proposition, whose truth value will depend on the truth values of the propositions that compose it.
To better understand how they work, it is helpful to recall an important concept: a proposition is a declarative sentence that can be unequivocally classified as true or false, but never both at the same time. Typical examples are: "2 is an even number" (true) or "5 is less than 3" (false). In logic, we usually represent them with lowercase letters like p, q, r, etc.
Just as in arithmetic we combine numbers through operations, in logic we combine propositions using connectives. The difference is that instead of getting a number as a result, we get a compound proposition, whose truth value is defined based on the initial propositions.
In propositional logic, the most common logical connectives are negation (not), conjunction (and), disjunction (or), the conditional (if... then), and the biconditional (if and only if). For each of them, there are specific symbols and a clear way to know when they are true and when they are false.
A fundamental aspect is that compound propositions can be joined again with other connectives, allowing us to create increasingly complex logical expressions. Because of this, logical connectives become a crucial part of mathematical reasoning, being essential for constructing arguments, carrying out proofs, and solving problems rigorously.
Table of Contents
Table of Logical Connectives
| Symbol | Logical Connective | Meaning |
|---|---|---|
| ¬ (also ~) | Negation ¬p | not p it is not the case that p it does not happen that p it is false that p |
| ∧ | Conjunction p ∧ q | p and q p although q p but q p however q p nevertheless q p despite q |
| ∨ | Disjunction p ∨ q | p or q or both either p or q |
| ⊻ | Exclusive Disjunction (or symmetric difference) p ⊻ q | p or q, but not both either p or q, but not both |
| → | Conditional (or implication) p → q | if p, then q p only if q p is sufficient for q q is necessary for p not p unless q |
| ↔ | Biconditional (or double implication) p ↔ q | p if and only if q p is necessary and sufficient for q p is equivalent to q |
Negation
The negation of the proposition p is the proposition ¬p (read as "not p"). The negator has the same meaning as the word "not" in ordinary language. When we negate a statement, our intention is to say that the statement is false. If a proposition is true, its negation is false; if a proposition is false, its negation is true.
We represent the truth conditions of this connective using a table. The initial column lists the possible truth values of a given statement p. The next column indicates the truth values that correspond to the negation of the statement. For the true value, the letter "T" is used, and for the false value, the letter "F" is used; in other contexts, "1" may be used for true and "0" for false.
| p | ¬p |
|---|---|
| T | F |
| F | T |
Example 1
p: "The Moon orbits the Earth"
¬p: "The Moon does not orbit the Earth"
The proposition p is true, because the Moon does orbit the Earth, therefore the proposition ¬p is false.
Example 2
q: "Fish can breathe out of water"
¬q: "It is not the case that fish can breathe out of water"
The proposition q is false, which causes the proposition ¬q to be true.
Example 3
r: "5 is an even number"
¬r: "5 is an odd number"
In this case, the original proposition is false and its negation is true.
Example 4
If we have a negated proposition ¬p, we can negate it again, generating the proposition ¬(¬p). Thus, if we start with:
p: "7 is a prime number"
We negate it to get:
¬p: "It is not the case that 7 is a prime number"
And we negate it again:
¬(¬p): "It is not the case that it is not the case that 7 is a prime number"
Because negating p once inverts its truth value, by negating the negation we inverted it again, returning to the initial state. We can check this by looking at the truth table:
| p | ¬p | ¬(¬p) |
|---|---|---|
| T | F | T |
| F | T | F |
When two propositions have the same truth value for every possible interpretation, they are said to be equivalent and are symbolized with "≡". Thus, we have that ¬(¬p) ≡ p, this is known as the law of involution or double negation. There are other logical laws related to negation that we will see later.
Note: negation is known as a unary connective, since it negates one proposition and does not connect it with another. In contrast, the other operators are called binary connectives, as they have a dual scope: to the right and to the left, that is, they affect two variables.
Conjunction
The conjunction of propositions p and q is the proposition p ʌ q (read as "p and q"). The meaning of the conjunction operator is identical to that of "and" in ordinary language. A conjunction is true when its components are true; it is false in any other case.
We represent the truth conditions using a table analogous to the previous one. In the first two columns, the four possible combinations of truth and falsity of propositions p and q are indicated in order. The third column indicates the truth values that correspond to each case.
| p | q | p ∧ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Example 1
Let p be the proposition: "The piano is a musical instrument" and q be: "2 is an even number", then:
p ʌ q: "The piano is a musical instrument and 2 is an even number"
The proposition p ʌ q is true because both p and q are true propositions.
Example 2
Let p: "The sky is red" and q: "2 + 2 = 4", their conjunction is:
p ʌ q: "The sky is red and 2+2 = 4"
The compound proposition p ʌ q is false because, although q is true, p is false.
Example 3
Let's define p: "8 is an odd number" and q: "8 is a negative number", we form the conjunction:
p ʌ q: "8 is an odd number and is negative"
Since it is not true that 8 is odd and it is also not true that 8 is negative, the conjunction p ʌ q is false.
Example 4
Let p: "4 is an even number", q: "-2 is a negative number" and r: "2.5 is an integer".
p ʌ q: "4 is an even number and -2 is a negative number"
p ʌ r: "4 is an even number and 2.5 is an integer"
The compound proposition p ʌ q is true because p and q are true. In contrast, p ʌ r is false because r is false. We can also form a conjunction with more than two propositions:
p ʌ q ʌ r: "4 is an even number, -2 is a negative number, and 2.5 is an integer"
The proposition p ʌ q ʌ r is false because, although p and q are true, r is false. If any of the parts is false, the entire conjunction is false.
We can also apply negations to conjunctions, for example:
¬(p ʌ q): "It is not the case that '4 is an even number and -2 is a negative number'"
This proposition is false, because the original conjunction was true. In contrast:
¬(p ʌ r): "It is false that '4 is an even number and 2.5 is an integer'"
The proposition is true because the original conjunction was false. The negation of a conjunction means that it is not the case that both propositions are simultaneously true, that is, at least one of them must be false (or both). Indeed: the part that says 2.5 is an integer is false. Although the part that states 4 is even is true, what is not true is that both propositions are true.
It is important to apply parentheses correctly, as a proposition ¬(p ʌ q) is not the same as ¬p ʌ q or p ʌ ¬q. Also, the order in which the propositions appear in a conjunction does not change its meaning, that is, conjunction is commutative: p ʌ q ≡ q ʌ p. This can be confirmed by creating the corresponding truth table.
Inclusive Disjunction
The disjunction of p and q is the proposition p ∨ q (read as "p or q"). The disjunction operator can be partially considered as a formal language translation of the word "or" from ordinary language. The disjunction of two propositions is true when at least one of those propositions is true (and when both are); it is false when both are false.
| p | q | p ∨ q |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
The truth conditions for disjunction are the "counterpart" to the truth conditions for conjunction. Also, the symbol for disjunction (∨) is the inverted image of the conjunction symbol (ʌ).
To prove the truth of a conjunction, one must prove the truth of all its members; to prove the truth of a disjunction, it is sufficient to prove the truth of one. The reverse is true for falsity: the falsity of a conjunction is established by proving the falsity of one of its members; whereas the falsity of a disjunction requires proving the falsity of all of them.
Example 1
Let p: "The Sun is a planet" and q: "The Earth is a planet".
p ∨ q: "The Sun is a planet or the Earth is a planet"
The proposition is true because q is true.
Example 2
Let's define p: "Fish can fly" and q: "3 is an even number", then:
p ∨ q: "Fish can fly or 3 is an even number"
The proposition p ∨ q is false because both p and q are false.
Example 3
Let p: "4 is an even number", q: "-2 is a negative number" and r: "2.5 is an integer". We can form:
p ∨ q: "4 is an even number or -2 is negative"
The proposition p ∨ q is true because both p and q are true. We can also construct:
p ∨ q ∨ r : "4 is an even number or -2 is negative or 2.5 is an integer"
The above statement is true because at least one of the propositions that compose it is true (in this case, p and q are), even though the last one is false.
Just as we saw before, we can apply negations to this connective, and also combine it with conjunctions or other connectives that we will see later. For example:
¬(p ∨ q): "It is not the case that '4 is an even number or -2 is negative'"
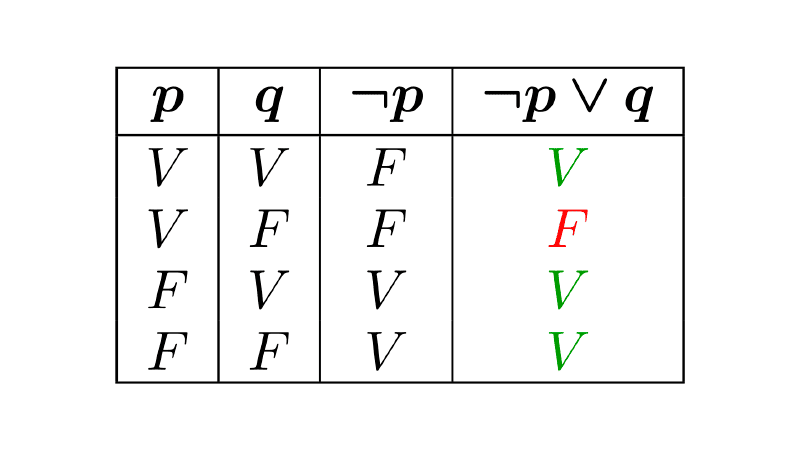
The proposition ¬(p ∨ q) is false because p ∨ q is true and the negation inverts its truth value. The negation of a disjunction means it is not true that any of the component propositions is true, but rather that both must be false. As can be seen in the truth table, the only case where ¬(p ∨ q) is true is when both p and q are false.
| p | q | p ∨ q | ¬(p ∨ q) |
|---|---|---|---|
| T | T | T | F |
| T | F | T | F |
| F | T | T | F |
| F | F | F | T |
Disjunction fulfills the commutative property, meaning the order of the propositions does not alter the meaning: p ∨ q ≡ q ∨ p.
Exclusive Disjunction
The exclusive disjunction of p and q is the proposition p ⊻ q (read as "p or q, but not both"). It is true when only one of the two propositions is true; it is false if both are false or if both are true simultaneously.
| p | q | p ⊻ q |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
This connective can be considered as the formal language translation of the word "or" in its exclusive sense, that is, when one wants to indicate that one thing happens or another happens, but not both at the same time. It differs from the other disjunction mainly for this reason.
Example 1
Let p: "4 is an even number" and q: "6 is an even number"
p ⊻ q: "4 is an even number or 6 is an even number, but not both"
The proposition p ⊻ q is false because p and q are simultaneously true.
Example 2
Let p: "The Earth is flat" and q: "The Earth is spherical"
p ⊻ q: "The Earth is flat or it is spherical, but not both"
In this case, p ⊻ q is true because only q is true while p is false.
Conditional (or Implication)
The implication or conditional of propositions p and q is the proposition p → q (read as "if p then q" or "p implies q"). The implication operator can be considered a partial formalization of the ordinary language phrase "if..., then...". The expression preceding the symbol is called the antecedent (p), and the one that follows, the consequent (q).
An implication is true when its antecedent is false or when its consequent is true; it is false when its antecedent is true and its consequent is false.
| p | q | p → q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Example 1
Let p: "John passes his exam" and q: "John's mother will give him a chocolate bar". We can form:
p → q: "If John passes his exam, then his mother will give him a chocolate bar"
The conditional connective acts like a promise: the only way to break a promise is if the one who promised something doesn't fulfill it. In this example, the only way the promise is not kept is if John passes the exam but his mother does not give him the chocolate. In that case, p will be true and q false, making p → q a false proposition.
In any other case, the promise is kept:
- John passes the exam (p is T) and his mother gives him the chocolate (q is T), then p → q is true.
- John does not pass his exam (p is F) and his mother still gives him the chocolate (q is T), then p → q is true.
- John does not pass his exam (p is F) and his mother does not give him the chocolate (q is F), making p → q true.
Note: one might think the second case is incorrect since John does not pass but still receives the gift. In reality, the initial promise was that if he passed, he would receive the gift, but it says nothing about what happens if he doesn't pass. Therefore, if John does not pass, his mother is free to decide whether or not to give him the gift as she is not breaking the initial promise.
Example 2
Let p: "Cats can fly" and q: "4 is an even number". We can form the implication
p → q: "If cats can fly, then 4 is an even number"
The proposition p → q is true because the antecedent p is false, so it doesn't matter what the truth value of the consequent q is, the implication will be true anyway.
The example may clash with our idea that in an implication there should be some relationship between the content of the antecedent and the consequent. In this case, cats have nothing to do with even numbers, but mathematical logic is not concerned with the content of propositions, but only focuses on their potential to be true or false. In other words, the mathematical conditional should not be interpreted as a cause-and-effect relationship.
Formulation of Theorems
The implication is one of the most used connectives in the formulation of mathematical theorems. Its typical structure is hypothesis → conclusion, where the hypothesis is the initial condition and the conclusion is what must be met whenever the hypothesis is true.
In this sense, if the hypothesis is met, the conclusion must necessarily be met as well; however, if the hypothesis is not met, the theorem remains valid even though the conclusion may be true or false.
For example, let's consider the following statement:
“If a number is a multiple of 4, then it is even”
Here the hypothesis is "the number is a multiple of 4" and the conclusion is "the number is even". The theorem is correct: whenever a number is a multiple of 4, it will also be even. However, if the hypothesis is not met, as in the case of the number 5 (which is not a multiple of 4), the theorem is not invalidated.
Let's think about the number 6. This number is not a multiple of 4, yet it is even. In this case, the theorem is still valid because the hypothesis was not met. The theorem does not say that every even number must be a multiple of 4; it only states that if a number is a multiple of 4, then it is even.
Thus, the conditional reflects the internal logic of theorems: it guarantees validity when the hypothesis is met, but demands nothing when it is not.
Associated Implications
Given the direct implication p → q, these are its associates:
- q → p is the converse implication, where we switch the propositions.
- ¬p → ¬q is the inverse implication, where we negate both propositions without changing their order.
- ¬q → ¬p is the contrapositive implication, where we switch and negate both propositions.
Every implication is equivalent to its contrapositive, that is p → q ≡ ¬q → ¬p. With the example of the theorem p → q: "If a number is a multiple of 4, then it is even," we can form:
Converse: q → p: "If a number is even, then it is a multiple of 4". This proposition is false; a counterexample is 6, which is even but not a multiple of 4.
Inverse: ¬p → ¬q: "If a number is not a multiple of 4, then it is not even". This statement is also false because, for example, 10 is not a multiple of 4 but it is even.
Contrapositive: ¬q → ¬p: "If a number is not even, then it is not a multiple of 4". This proposition is true since no number that is not even can be a multiple of 4.
A real-life example can be made with the propositions p: "It is raining" and q: "The yard is wet":
- p → q: "If it is raining, then the yard is wet".
- q → p: "If the yard is wet, then it is raining".
- ¬p → ¬q: "If it is not raining, then the yard is not wet".
- ¬q → ¬p: "If the yard is not wet, then it is not raining".
The converse and inverse implications are not equivalent to the original, as the yard could be wet even when it is not raining (someone could wet it by pouring water). However, if the yard is not wet, we can certainly assure that it is not raining.
Biconditional (or Double Implication)
The double implication of propositions p and q is the proposition p ↔ q (read as "p if and only if q"). This connective can be considered as the formal language translation of the phrase "if and only if" and also "is equivalent to". It is used in establishing definitions of equivalences and in expressing necessary and sufficient conditions.
A double implication is true when its two components have the same truth value, that is, when both are true or both are false; and it is false otherwise, that is, when one of them is true and the other is false.
| p | q | p ↔ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
The biconditional is logically equivalent to the conjunction of two implications:
p ↔ q ≡ (p → q) ʌ (q → p)
Example 1
Let p: "It is raining" and q: "The street is wet", we can form the proposition:
p ↔ q: "It is raining if and only if the street is wet"
If it is true that it is raining (p is T) and it is also true that the street is wet (q is T), the proposition p ↔ q is true. If it is not raining (p is F) and the street is not wet (q is F), the statement p ↔ q is also true. However, if either of the two propositions p or q is false, the biconditional will be false, that is, when it is raining (p is T) and the street is not wet (q is F) or when the street is wet (q is T) without it raining (p is F).
Example 2
Let p: "A number is even" and q: "A number is divisible by 2".
p ↔ q: "A number is even if and only if it is divisible by two"
If a number is even, then it is divisible by 2 (by definition); and if a number is divisible by 2, then it is even. The relationship works in both directions, therefore the proposition p ↔ q is true.
Example 3
Let's define p: "A triangle is equilateral" and q: "The three sides of a triangle are equal"
p ↔ q: "A triangle is equilateral if and only if its three sides are equal"
If a triangle is equilateral, its three sides are equal; and if the three sides of a triangle are equal, then we say it is equilateral. Since this holds in both directions, the biconditional p ↔ q is true.
Example 4
Let p: "The sum of two numbers is even" and q: "Two numbers are even".
p ↔ q: "The sum of two numbers is even if and only if the two numbers are even"
This proposition is false because, while it is true that the sum of two even numbers is always an even number (for example 2+2=4), the sum of two odd numbers also results in an even number (like 3+1=4).
The most common symbols for the biconditional are "↔" and "⇔". Also, the equivalence symbol "≡" that we have used so far is the same as a biconditional. The expression "if and only if" is commonly abbreviated as "iff". For example: "A triangle is equilateral iff its three sides are equal".
Hierarchy of Logical Connectives
When using logical symbols, a hierarchy is established among them (also called precedence or priority) which indicates which operations are performed first, thus avoiding the excessive use of parentheses. The convention for evaluating operators is as follows:
- Negation (¬).
- Conjunction (∧).
- Disjunction (∨).
- Conditional (→).
- Biconditional (↔).
Grouping symbols (parentheses, brackets, and braces) can alter the precedence, and are always evaluated first.
Examples
- ¬p ∧ q is interpreted as (¬p) ∧ q.
- p ∧ q ∨ r is interpreted as (p ∧ q) ∨ r.
- ¬p ∧ q → r is interpreted as [(¬p) ∧ q ] → r.
- p ∧ q → r ∨ s is interpreted as (p ∧ q) → (r ∨ s).
- p ↔ ¬q ∨ r is interpreted as p ↔ (¬q ∨ r).
- ¬p → q ↔ r ∧ s → t should be understood as (¬p → q) ↔ [(r ∧ s) → t].
Note that negation only affects the immediate proposition, unless modified by parentheses, for example, ¬(p ∧ q).
Practice Exercises
Exercise: given the propositions:
p: "The sky is cloudy".
q: "A triangle has three sides".
r: "It is raining".
s: "The doorbell rings".
t: "The dog barks".
Formulate the following compound propositions:
- ¬p ∧ q
- s → ¬(t ∨ r)
- p ⊻ s → t
- q ↔ ¬t
- ¬(r ∧ s)
- t → s
- p → q ∧ r
Solutions:
- ¬p ∧ q: "The sky is not cloudy and a triangle has three sides".
- s → ¬(t ∨ r): "If the doorbell rings, then it is not the case that the dog barks or it is raining".
- p ⊻ s → t: "If the sky is cloudy or the doorbell rings (but not both), then the dog barks".
- q ↔ ¬t: "A triangle has three sides if and only if the dog does not bark".
- ¬(r ∧ s): "It is false that it is raining and the doorbell rings".
- t → s: "If the dog barks, then the doorbell rings".
- p → q ∧ r: "If the sky is cloudy, then a triangle has three sides and it is raining".
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
More information about each connective
Leave a Reply


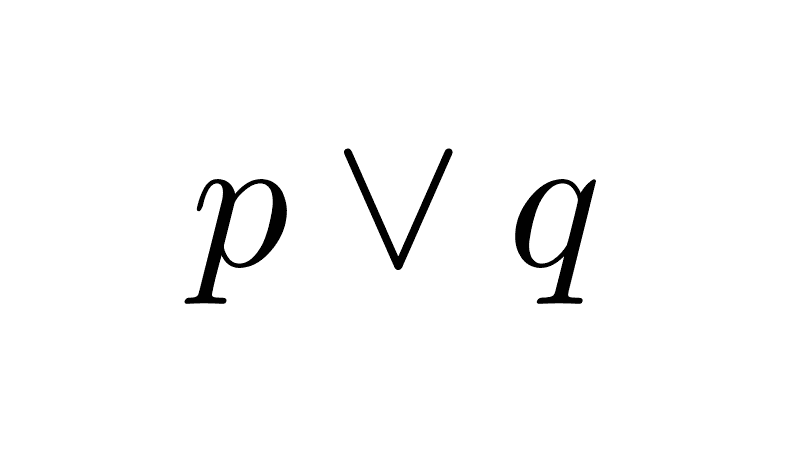
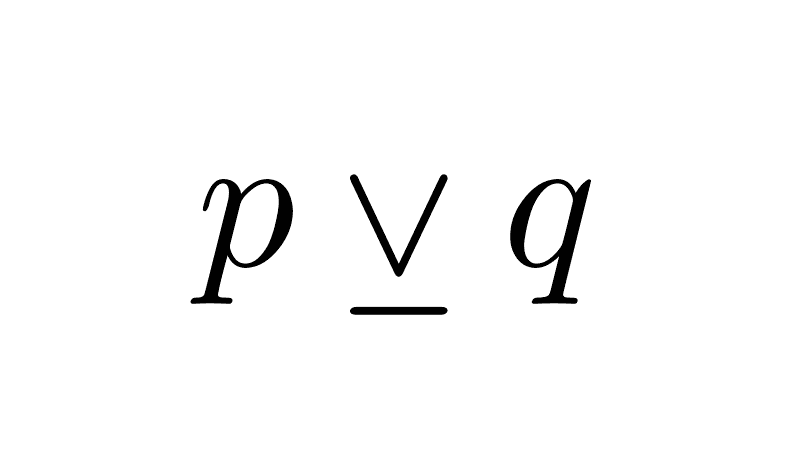
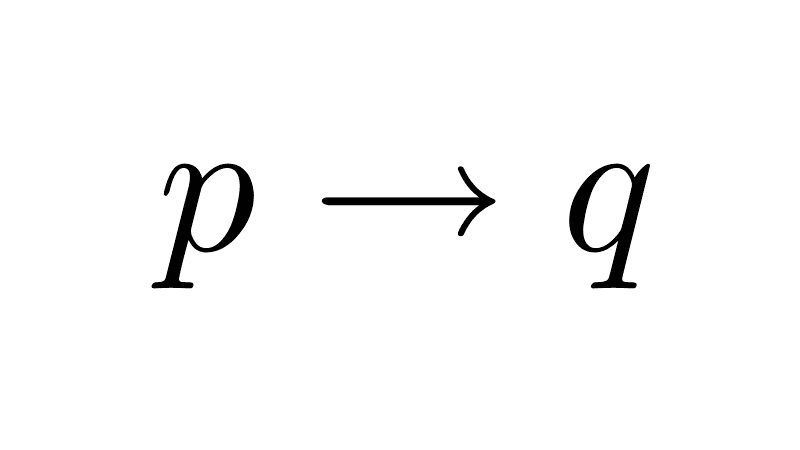
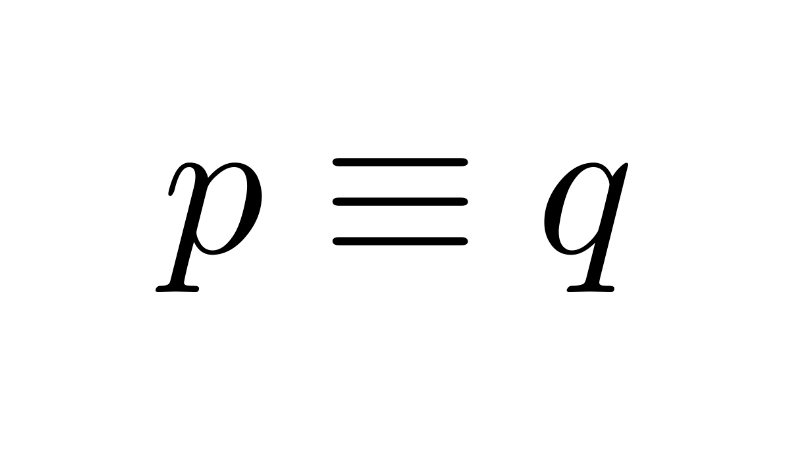
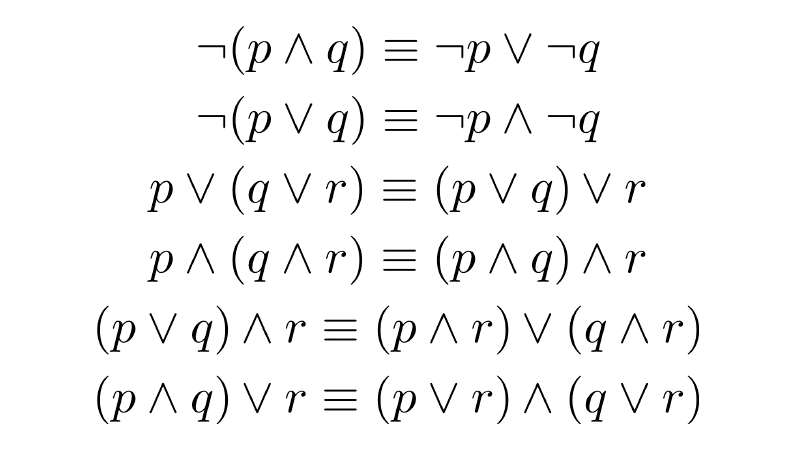
Related posts