Logical Laws
A logical law (also called a tautology) is a compound proposition that is always true, regardless of the truth value of its constituent propositions. These laws are universal principles of logic, as they express equivalences and relationships that hold true in every possible case.
Their usefulness lies in their ability to transform and simplify logical expressions, as well as to construct rigorous proofs in mathematics and philosophy. To verify that a proposition is a logical law, one simply needs to construct its truth table, which must show that it evaluates to true for all possible combinations of truth values.
Table of Contents
Fundamental Laws
The fundamental laws of logic are the basic principles of rational thought. They are universal rules that guarantee the coherence and validity of reasoning, serving as a starting point for the entire subsequent development of formal logic. These laws are not mere conventions but express necessary conditions for knowledge to be communicated, discussed, and rigorously substantiated.
Laws of Identity
These laws state that every proposition is identical to itself. It asserts that if a proposition is true, then it is true, and if it is false, then it is false. This principle ensures that a concept or proposition cannot change its truth value during the course of an argument.
p ≡ p
p → p
Examples: "A dog is a dog," "If it rains, then it rains."
Law of Non-Contradiction
It is impossible for a proposition to be both true and false at the same time and under the same circumstances. This principle is crucial for avoiding inconsistencies in reasoning.
¬ (p ∧ ¬p)
Example: "It is impossible for it to be raining and not raining at the same time."
Law of the Excluded Middle
A proposition is either true or false; there is no third option. This principle is the basis for proof by cases and proof by contradiction (reductio ad absurdum).
p ∨ ¬p
Example: "That animal is either a dog or not a dog."
Main Laws of Propositional Logic
The laws of propositional logic, also known as logical equivalences, are fundamental principles that govern the manipulation and simplification of propositions. These laws establish equivalence relations between logical formulas, allowing one expression to be substituted for another without altering its truth value.
| Name | Symbolism | Description |
|---|---|---|
| Involution or Double Negation | ¬(¬p) ≡ p | The negation of the negation of a proposition is equivalent to the proposition itself. |
| De Morgan's Law for Conjunction Negation | ¬(p ∧ q) ≡ ¬p ∨ ¬q | The negation of a conjunction is equivalent to the disjunction of the negations. |
| De Morgan's Law for Disjunction Negation | ¬(p ∨ q) ≡ ¬p ∧ ¬q | The negation of a disjunction is equivalent to the conjunction of the negations. |
| Commutativity | p ∨ q ≡ q ∨ p p ∧ q ≡ q ∧ p | The order of the propositions does not alter the result in a conjunction or disjunction. |
| Associativity | p ∨ (q ∨ r) ≡ (p ∨ q) ∨ r p ∧ (q ∧ r) ≡ (p ∧ q) ∧ r | It is permissible to group propositions in a chain of conjunctions or disjunctions. |
| Distributivity | (p ∨ q) ∧ r ≡ (p ∧ r) ∨ (q ∧ r) (p ∧ q) ∨ r ≡ (p ∨ r) ∧ (q ∨ r) | Conjunction is distributive over disjunction, and vice versa. |
| Idempotence | p ∧ p ≡ p p ∨ p ≡ p | The conjunction or disjunction of a proposition with itself is equivalent to the proposition itself. |
| Absorption Laws | p ∨ (p ∧ q) ≡ p p ∧ (p ∨ q) ≡ p | The disjunction of a proposition with a conjunction where it also appears is equivalent to the original proposition; the same holds if the connectives are swapped. |
Laws Related to Conditionals
The conditional is one of the most important logical connectives and, at the same time, one of the least intuitive for everyday reasoning. Its analysis is essential in logic and mathematics, as a large part of formal proofs and arguments are built upon conditional statements. For this reason, it is crucial to understand not only its formal definition but also the most relevant equivalences that allow it to be transformed into other logical expressions.
| Name | Symbolism | Description |
|---|---|---|
| Definition of Conditional | p → q ≡ ¬p ∨ q | A conditional is equivalent to the disjunction of the negation of the antecedent and the consequent. |
| Negation of a Conditional | ¬(p → q) ≡ p ∧ ¬q | The negation of a conditional is equivalent to the conjunction of the antecedent and the negation of the consequent. |
| Law of Contrapositive, Contraposition, or Transposition | (p → q) ≡ (¬q → ¬p) | A logical implication can be expressed in its contrapositive form by negating and swapping the order of the propositions. |
| Definition of Biconditional or Equivalence | (p ↔ q) ≡ [(p → q) ∧ (q → p)] (p ↔ q) ≡ [(p ∧ q) ∨ (¬p ∧ ¬q)] | The biconditional is equivalent to the conjunction of two conditionals: one forward and one backward. |
| Negation of a Biconditional | ¬(p ↔ q) ≡ (p ∧ ¬q) ∨ (¬p ∧ q) | Negating an equivalence is the same as stating that one proposition is true and the other is false, or vice versa. |
| Contraposition of a Biconditional | (p ↔ q) ≡ (¬q ↔ ¬p) | The biconditional of two propositions is equivalent to the biconditional of their negations. |
| Law of Permutation | [p → (q → r)] ≡ [q → (p → r)] | The order of the antecedents in a chained implication can be reversed without altering its logical value. |
| Expansion Laws | (p → q) ≡ [(p ∨ q) ↔ q] (p → q) ≡ [(p ∧ q) ↔ p] | A conditional can be expressed as a biconditional between the conjunction (or disjunction) of its components and the consequent (or the antecedent). |
Inference Rules
Inference rules are patterns that allow a new, valid proposition to be deduced from one or more premise propositions that are assumed to be true.
| Name | Symbolism |
|---|---|
| Modus Ponens | [(p → q) ∧ p] → q |
| Modus Tollens | [(p → q) ∧ ¬q] → ¬p |
| Syllogism | (p → q) → [(q → r) → ( p → r)] |
| Disjunctive Syllogism | [(p ∨ q) ∧ ¬p] → q [(p ∨ q) ∧ ¬q] → p |
| Transitivity or Hypothetical Syllogism | [(p → q) ∧ (q → r)] → (p → r) [(p ↔ q) ∧ (q ↔ r)] → (p ↔ r) |
| Simplification | p ∧ q → p p ∧ q → q |
| Addition | p → p ∨ q q → p ∨ q |
| Constructive Dilemma | [( p ∨ q) ∧ ( p → r) ∧ (q → r)] → r |
| Second Law of Constructive Dilemma | [(p → q) ∧ (r → s) ∧ (p ∨ r)] → (q ∨ s) |
| Destructive Dilemma | [(p → q) ∧ (r → s) ∧ (¬q ∨ ¬s) ] → (¬p ∨ ¬r) |
| Law of Cases | [(p → q) ∧ (¬p → ¬q)] → q |
| Exportation | [(p ∧ q) → r] ≡ [p → (q ∧ r)] |
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

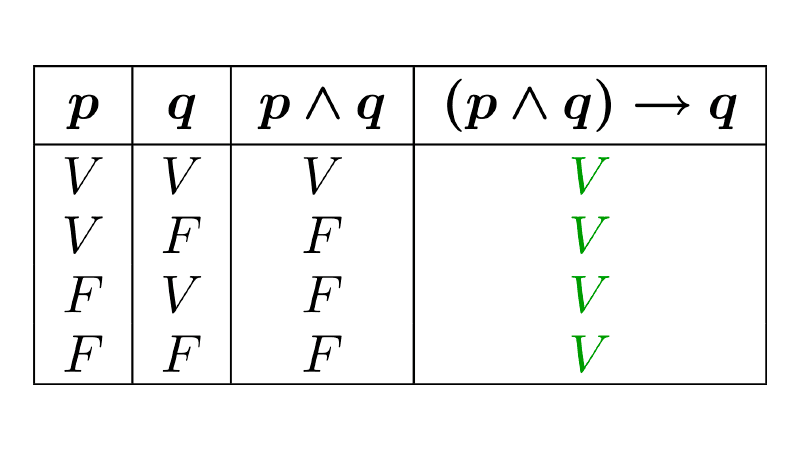
Related posts