Cartesian Product
The Cartesian product of two sets A and B, denoted as A×B, is the set whose elements are all ordered pairs where the first component belongs to A and the second to B.
A × B = {(a, b) | a ∈ A ∧ b ∈ B}
Table of Contents
Examples
1) Given the sets A = {1, 2} and B = {a, b}, the Cartesian product is:
A × B = {(1, a), (1, b), (2, a), (2, b)}
2) Let C = {x, y, z} and D = {0, 1}, their Cartesian product is:
C × D = {(x, 0), (x, 1), (y, 0), (y, 1), (z, 0), (z, 1)}
3) The Cartesian product of the sets A = {a, b, c} and B = {1, 2} is the set:
A × B = {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)}
4) Given the set N (natural numbers) and the set B = {0, 1}, the Cartesian product between them will have infinitely many elements. Expressed in set-builder notation, it is:
N × B = {(n, b) | n ∈ N, b ∈ {0, 1} }
Some of the ordered pairs in this set are (1, 0), (2, 0), (1, 1), (5, 0), etc.
5) The set of rational numbers is defined as the Cartesian product of the set of integers (Z) and itself, excluding zero (Z*):
Q = Z × Z*
6) The set of complex numbers is defined as the Cartesian product of the set of real numbers (R) and itself:
C = R × R
The Cartesian product of a set with itself is:
A × A = A2 = {(a, b) | a ∈ A ∧ b ∈ A}
For example, with A = {1, 2}, we have A × A = A2 = {(1, 1), (1, 2), (2, 1), (2, 2)}.
An important point to note is that A × B is not the same as B × A (unless A = B).
Let's test this with A = {a, b, c} and B = {1, 2}:
A × B = {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)}
B × A = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)}
The set B×A is not equal to the set A×B because the components in an ordered pair cannot be swapped. In other words: the order in which the sets appear is important when calculating the Cartesian product.
Cartesian product of three sets
The Cartesian product of three sets A, B, and C is the set:
A × B × C = {(a, b, c) | a ∈ A ∧ b ∈ B ∧ c ∈ C}
This set is formed by ordered triples instead of ordered pairs.
Example: given the sets A = {1, 2}, B = {x}, and C = {a, b}, we have:
A × B × C = {(1, x, a), (1, x, b), (2, x, a), (2, x, b)}
How to calculate the Cartesian product
Let's look at some techniques we can use to facilitate the calculation of Cartesian products. These are only useful when dealing with sets containing few elements and we need to express the product in roster form. When dealing with infinite sets, it is more than sufficient to leave the Cartesian product expressed as in the definition, i.e., in set-builder notation.
Cartesian product of 2 sets
When dealing with ordered pairs, we can use a Cartesian coordinate plane to represent the elements of both sets and find their product. We place the elements of the first set on the horizontal axis and the elements of the second set on the vertical axis. Then, we form the corresponding ordered pairs.
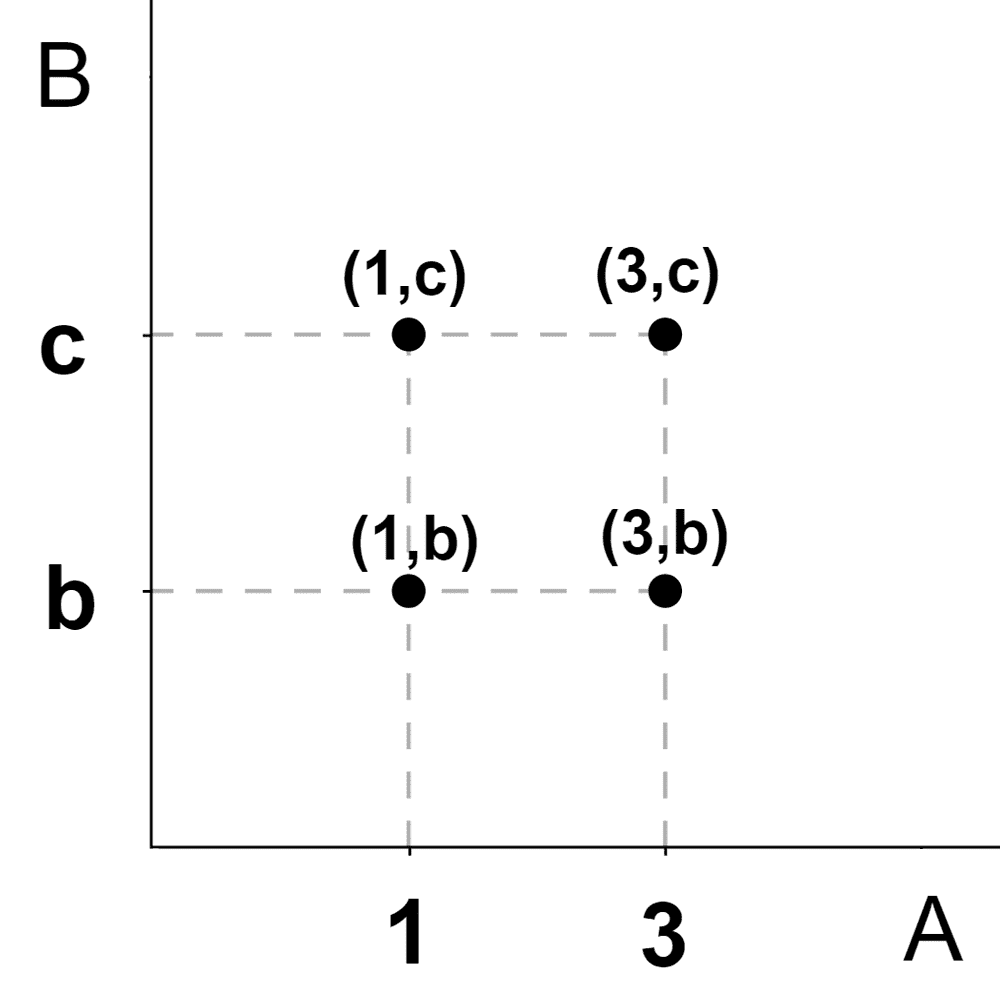
For example, let the sets be A = {1, 3} and B = {b, c}, and we want to calculate A×B. The Cartesian graph would look like this:
From this, we extract that A×B = {(1,b), (1,c), (3,b), (3,c)}. Another more compact method is to use a table that follows the same logic as the graph, like the following:
| c | (1, c) | (3, c) |
| b | (1, b) | (3, b) |
| A × B | 1 | 3 |
From here, we arrive at the same ordered pairs for the Cartesian product.
Cartesian product of 3 sets
In the case of three sets, the representation of A×B×C would not be on a plane, but in space, due to the three components of the triple. However, to avoid the complexity of making three-dimensional graphs, we can first calculate the product of the first two sets and then, using the resulting pairs, form the triples with the previous process. That is, calculate (A × B) × C.
Example: let A = {a, b, c}, B = {1, 2}, and C = {7, 8}. First, we calculate A×B:
| 2 | (a, 2) | (b, 2) | (c, 2) |
| 1 | (a, 1) | (b, 1) | (c, 1) |
| A × B | a | b | c |
So, A × B= {(a, 2), (b, 2), (c, 2), (a, 1), (b, 1), (c, 1)}. We now place these resulting pairs on the horizontal axis and the elements of C on the vertical axis:
| 8 | (a, 2, 8) | (b, 2, 8) | (c, 2, 8) | (a, 1, 8) | (b, 1, 8) | (c, 1, 8) |
| 7 | (a, 2, 7) | (b, 2, 7) | (c, 2, 7) | (a, 1, 7) | (b, 1, 7) | (c, 1, 7) |
| A × B × C | (a, 2) | (b, 2) | (c, 2) | (a, 1) | (b, 1) | (c, 1) |
From here, we can now extract all the triples of A × B × C = {(a, 2, 8), (b, 2, 8), (c, 2, 8), (a, 1, 8), (b, 1, 8), (c, 1, 8), (a, 2, 7), (b, 2, 7), (c, 2, 7), (a, 1, 7), (b, 1, 7), (c, 1, 7)}.
Properties of the Cartesian product
The Cartesian product operation follows certain properties related to set operations, some of which are:
| Property | Symbolic Notation |
|---|---|
| Distributivity over set union, intersection, and difference | (A ∪ B) × C = (A × C) ∪ (B × C) (A ∩ B) × C = (A × C) ∩ (B × C) (A - B) × C = (A × C) - (B × C) |
| Complement of the Cartesian product | (A × B)c = (Ac × Bc) ∪ (Ac × B) ∪ (A × Bc) |
| The Cartesian product of two sets is empty if and only if at least one of them is empty. | A × B = ϕ ↔ A = ϕ ∨ B=ϕ |
| Two sets A' and B' are subsets of A and B respectively if and only if their Cartesian product is a subset of the Cartesian product of A and B. | A' ⊆ A ∧ B' ⊆ B ↔ A' × B' ⊆ A × B |
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

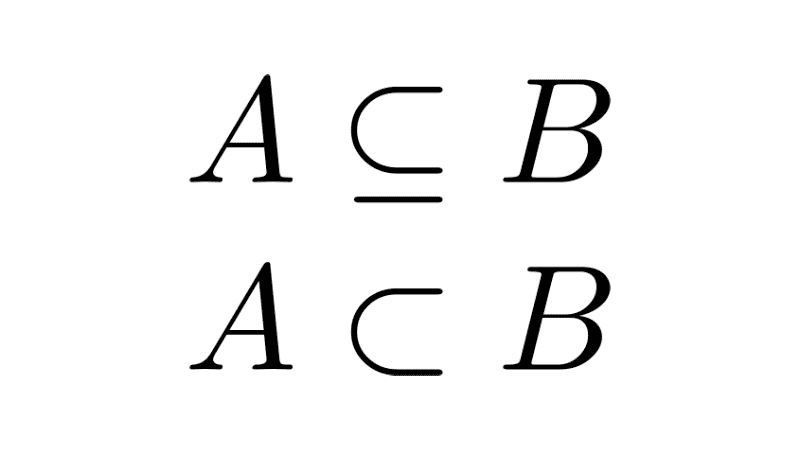

Related posts