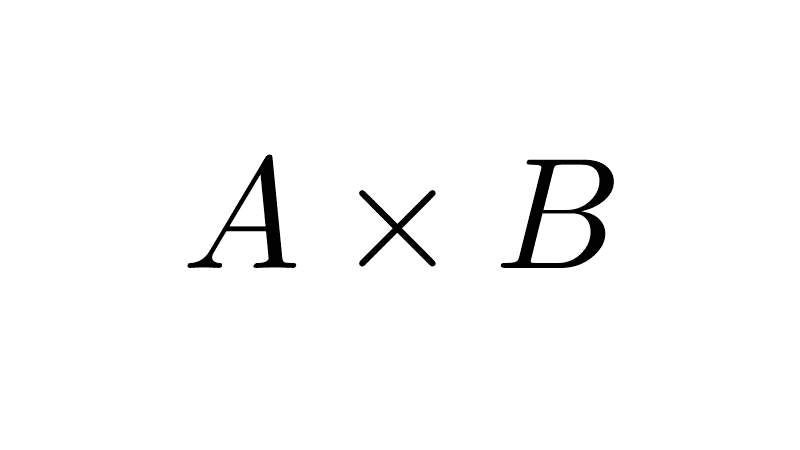
Empty Set
The empty set, also known as the null set, is a set that contains no elements. It is symbolized by Ø or by two braces with nothing inside { }.
Examples
The empty set can be expressed by set-builder notation, indicating a property that no element satisfies. It can also arise as the result of operations between sets.
- Ø = {x | x ≠ x}
- Ø = {x | 0 ⋅ x = 4}
- Ø = {x | x = 2 and x = 8}
- Ø = {x | x is a real number and x2 = -1}
- Ø = {x | x is a real number and |x| < 0}
- Ø = {x | x is an integer and 5 < x < 6}, because there is no integer between two consecutive integers.
- If A = {a, b} and B = {1, 2} then A ∩ B = Ø.
- The set of planets orbiting the Moon is Ø.
Properties
Some important properties of the empty set include:
- The empty set is a subset of any set, including itself. That is, Ø ⊆ A for any set A, and also Ø ⊆ Ø. This is because there are no elements in the empty set that are not in A.
- The empty set is finite, and its cardinality is zero: |Ø| = 0.
- The empty set is unique. If we assume that besides Ø, there is another empty set Ø’, then by the first property, it would be that Ø ⊆ Ø’ and Ø’ ⊆ Ø. Since there is mutual inclusion, both sets are equal: Ø = Ø’.
- The only subset of the empty set is itself. Symbolically, A ⊆ Ø if and only if A = Ø. In other words, the only element of the power set of the empty set is the empty set itself: P(Ø) = {Ø}.
- The empty set is an element of the power set of any set: Ø ∈ P(A) for any set A. This is due to the first property stated.
- The union of a set A with the empty set is simply A: A ∪ Ø = A.
- The intersection of a set A with the empty set is the empty set. A ∩ Ø = Ø.
- The difference of any set with itself is the empty set: A - A = Ø.
- The difference of any set with the empty set is the set itself: A - Ø = A.
- The complement of the empty set is the universal set: Ø’ = U; and the complement of the universal set is the empty set: U’ = Ø.
- The Cartesian product of any set with the empty set is the empty set. This is because no ordered pairs can be formed when one of the sets is empty.
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

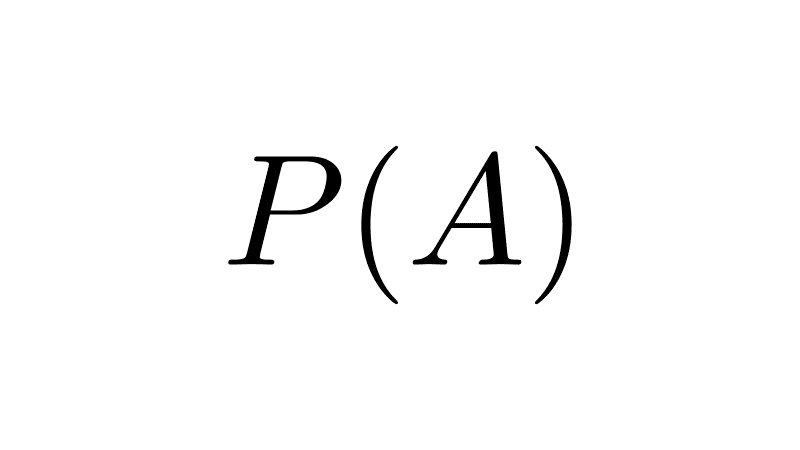
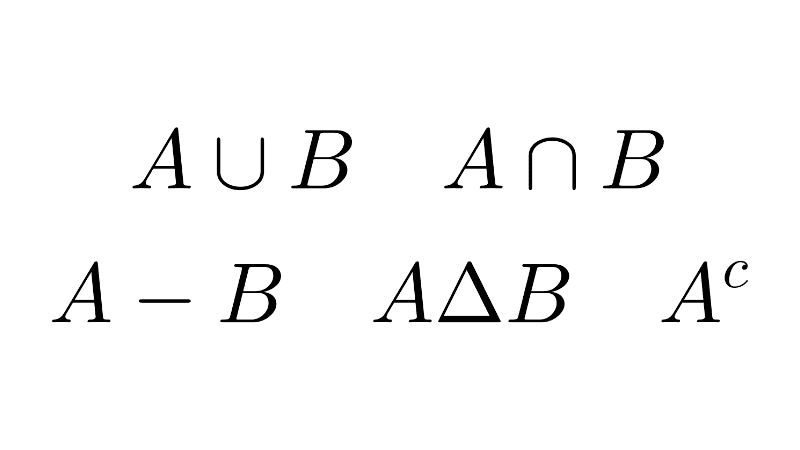
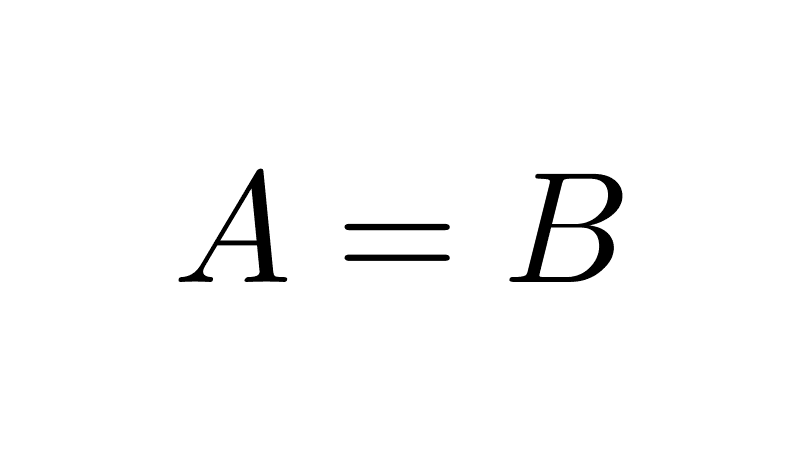
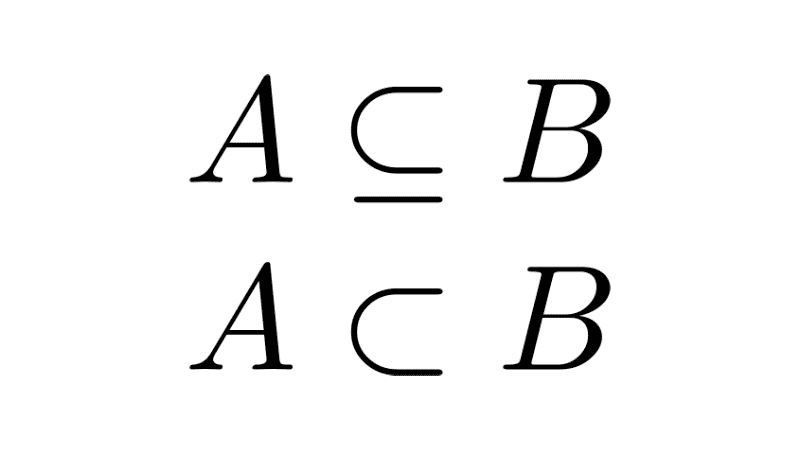
Related posts