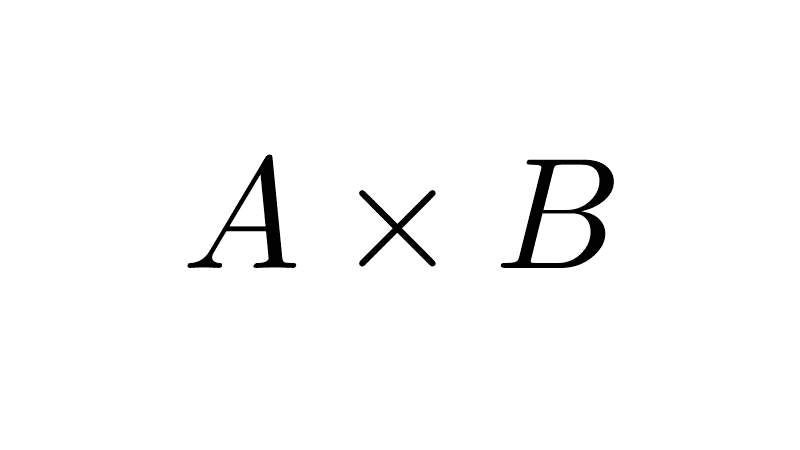
Subset of a Set
A subset is a collection of elements that are entirely contained within another set, which may or may not be larger. For example, the set {1, 2} is a subset of {1, 2, 3} because all elements of the first set are also in the second.
There are two types of subsets: proper and improper. A proper subset is one whose elements are within another set, but the latter has elements that are not in the former, meaning they cannot be equal sets. An improper subset is one that is identical to the original set.
Table of Contents
Formal Definition
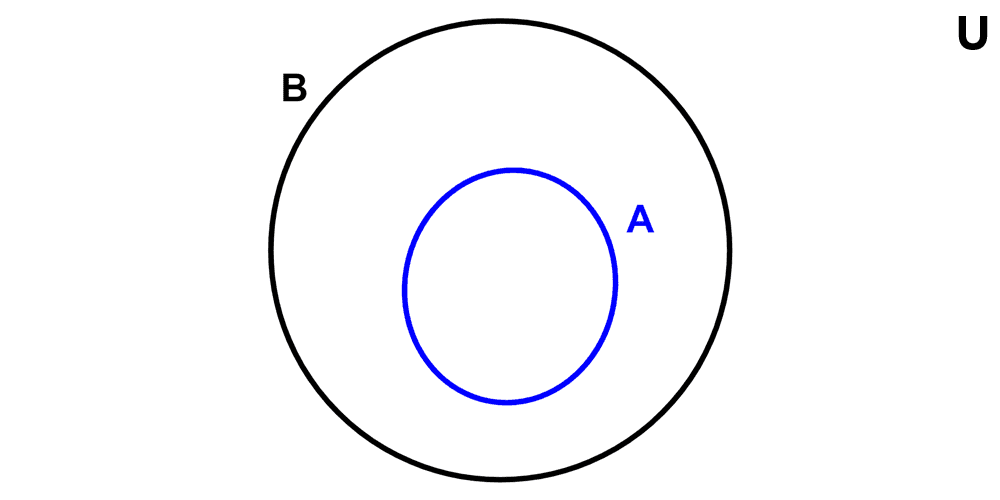
A set A is a subset of another set B if every element of A is also an element of B. This relationship is symbolized by ⊆ (inclusive subset):
A ⊆ B if and only if ∀x: (x ∈ A → x ∈ B)
We can also say that a set B is a superset of a set A (written as B ⊇ A) if and only if every element of A is also an element of B. In other words: B is a superset of A exactly when A is a subset of B.
If there is at least one element in A that is not in B, then A is said to not be a subset of B, symbolized as A ⊈ B.
Examples
- The set A = {a, b} is a subset of B = {a, b, c, d} because the elements of A are also within B, so A ⊆ B.
- The set of all mammals has the set of all human beings as a subset, because every human being is a mammal.
- The set C = {0, 1, 2, 3} is a subset of D = {-1, 0, 1, 2, 3, a, b} because every element of C is also contained in D, so C ⊆ D.
- The set of all plants is a subset of the set of all living beings.
- The set P = {p, q, r, s} is not a subset of Q = {p, r} because P has elements that are not in Q, so: P ⊈ Q. However, we can notice that Q is indeed a subset of P, so Q ⊆ P.
- The set M = {-1, 1} is a subset of N = {1, -1}: M ⊆ N; and, in turn, N is a subset of M: N ⊆ M. When this occurs, the sets are said to be equal: M = N. In other terms, M is an improper subset of N.
- The set of natural numbers is a subset of the set of integers, since every natural number is also an integer, so N ⊆ Z. However, since there are integers that are not natural numbers (negative numbers and zero), the reciprocal relationship is not true; Z is not a subset of N: Z ⊈ N.
- The set of all positive real numbers R+ is a subset of the real numbers, because every positive real number is also a real number: R+ ⊆ R.
- If we call T the set of all triangles, then the set E of equilateral triangles is a subset of T: E ⊆ T.
- The empty set is considered an improper subset of itself: ∅ ⊆ ∅. Also, the empty set is a subset of any set: ∅ ⊆ A for any set A.
To prove that a set is a subset of another, one must show that every element of the first is also an element of the second. To prove that a set is not a subset of another, it is sufficient to find one element in the first that is not in the second.
The set containing all subsets of A is called the power set of A, and is symbolized as P(A). If A has n elements, its power set has 2n elements. That is, the number of subsets of a set with n elements is 2n. For example, if A = {1, 2, 3}, its power set is P(A) = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}. In this case, the number of subsets is 23 = 8.
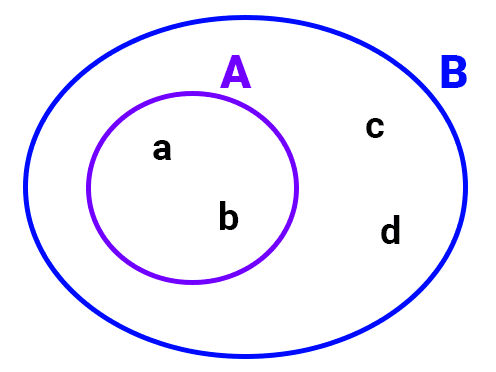
Proper Subset
A set is a proper subset of another if all elements of the first are also elements of the second, but there are elements in the second that are not in the first, meaning the sets cannot be equal. This relationship is symbolized by ⊂ (strict inclusion) or ⊊:
A ⊂ B if and only if ∀x: (x ∈ A → x ∈ B) and A ≠ B
If there is at least one element of A that is not in B, or if A and B are equal, then A is said to not be a proper subset of B, symbolized as A ⊄ B.
Examples
- The set A = {a, b} is a proper subset of B = {a, b, c, d} because the elements of A are also within B and there are elements in B that are not in A ("c" and "d"). Therefore, A ⊂ B. Note that it is also true that A ⊆ B.
- The set M = {-1, 1} is not a proper subset of N = {1, -1} because both sets are equal, so M ⊄ N. However, it is true that M ⊆ N, meaning M is a subset of N, but not a proper subset.
- The set of all Spanish-speaking human beings is a proper subset of the set of all human beings.
- The set of natural numbers, in addition to being a subset of the integers, is also a proper subset of it: N ⊂ Z.
- The set P of even numbers is a proper subset of the integers (P ⊂ Z), since there are integers that are not even.
- The set of rational numbers (Q) is a proper subset of the real numbers (R): Q ⊂ R, because there are irrational numbers (like π or √2) in R that are not in Q.
- The interval [0, 1] is a proper subset of the interval [-1, 2]: [0, 1] ⊂ [-1, 2], because [-1, 2] contains numbers less than 0 and greater than 1 that are not in [0, 1].
- The interval (5, 10) is a proper subset of the interval [5, 10), that is: (5,10) ⊂ [5,10), because the second set includes the number 5, which is not in the first.
- The set of all squares is a proper subset of the set of all rectangles (Squares ⊂ Rectangles), because a square is a special case of a rectangle, but there are rectangles that are not squares (those with sides of different lengths).
- The set of all circles is a proper subset of the set of all ellipses, since there are ellipses that are not circles.
Every proper subset is also a subset, as in the first example, but not every subset is a proper subset, as in the second example.
Properties of Subsets
Subsets comply with the properties of set inclusion:
- Reflexivity: Every set is a subset of itself, i.e., A ⊆ A.
- Antisymmetry: If a set is a subset of another and the second is also a subset of the first, then both sets are equal. That is, if A ⊆ B and B ⊆ A, then A = B.
- Transitivity: If a set is a subset of another, and that set is in turn a subset of a third, then the first set is also a subset of the third. That is, if A ⊆ B and B ⊆ C, then A ⊆ C.
- The empty set is a subset of any set, including itself. In other words, Ø ⊆ A and Ø ⊆ Ø.
- All sets are subsets of the universal set U: A ⊆ U.
Symbology
Below is a summary of the symbology used to refer to subsets.
| Symbol | Meaning |
|---|---|
| A ⊆ B | A is a subset of B |
| A ⊈ B | A is not a subset of B |
| B ⊇ A | B is a superset of A |
| A ⊂ B | A is a proper subset of B |
| A ⊄ B | A is not a proper subset of B |
Note: The symbols A ⊆ B and A ⊂ B are not used uniformly in mathematics. Sometimes the symbol ⊆ is used for subsets and other times for proper subsets; the same occurs with the symbol ⊂. It is also important to recognize that containment symbols (⊆ and ⊂) are used to relate two sets to each other, not to relate an element to a set. For that, the symbol ∈ (read as "belongs to") is used.
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

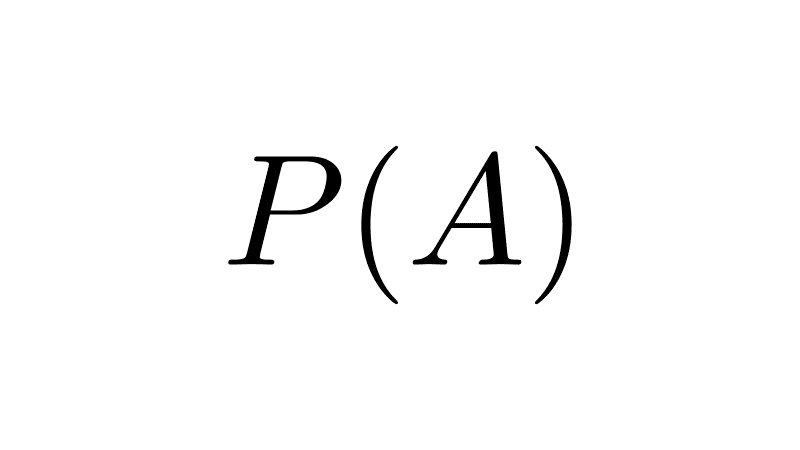
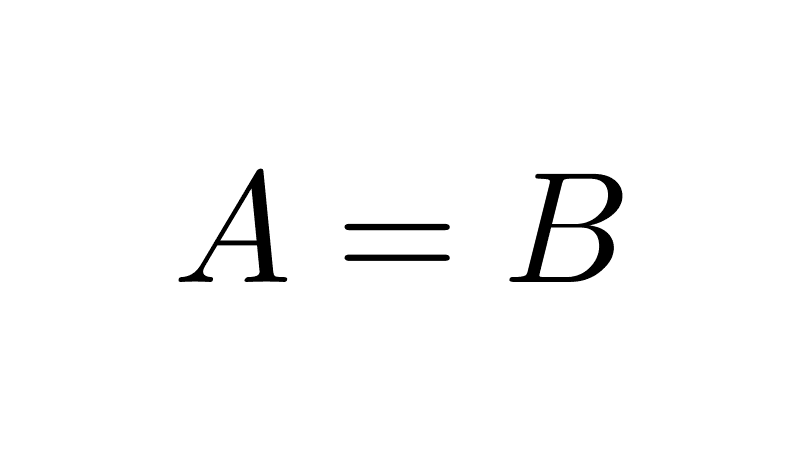
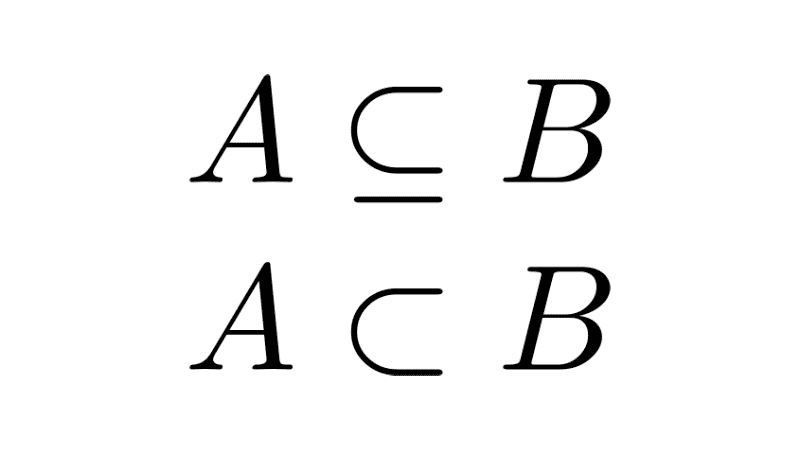
Related posts