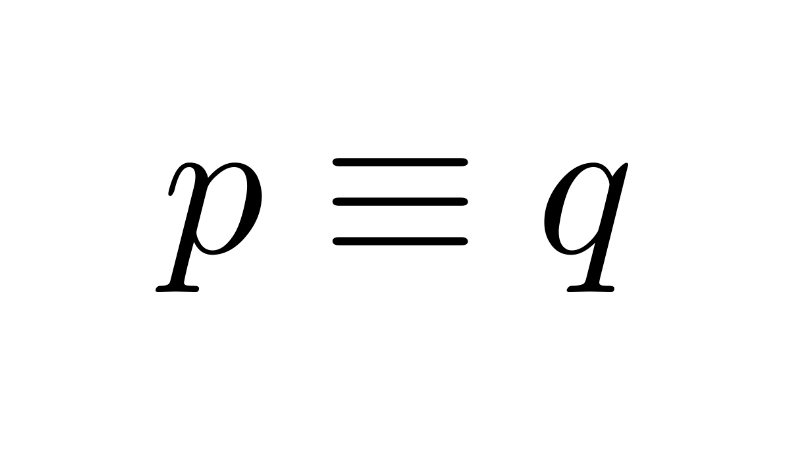
Contradiction in Mathematical Logic

In propositional logic, a contradiction is a compound proposition that is false regardless of the truth values of the simple propositions that make it up.

A contradiction is a scenario in which two or more statements cannot be simultaneously true in the same context, for example: "it is cold and it is not cold." This sentence expresses an obvious logical contradiction, as it asserts that something is and is not the case at the same time.

Logical contradictions are fundamental in mathematical logic as they allow, among other things, for identifying invalid arguments: if an argument leads to a contradiction, it is proven to be invalid, regardless of the truth of its premises.

Truth Table of a Contradiction

To verify if a proposition is contradictory, we can construct a truth table. If the column for the proposition is false for all interpretations of the variables, then it is a contradiction.

For example, the following is the truth table for the proposition p ∧ ¬p:

p	¬p	p ∧ ¬p
T	F	F
F	T	F

We observe that the compound proposition p ∧ ¬p is false in both rows, regardless of whether p is true or false. This means that the compound proposition is a contradiction.

Contradictions differ from tautologies, which are always true, and from contingencies, which are true in some cases and false in others. Every contradiction is the negation of a tautology, and every tautology is the negation of a contradiction. 

To obtain the tautology associated with the contradiction p ∧ ¬p, we just need to negate that proposition. Thus, the proposition ¬(p ∧ ¬p) is a tautology or logical law, known as the "principle of non-contradiction," which states that a proposition cannot be true and false simultaneously. Using one of De Morgan's laws, ¬(p ∧ ¬p) can be written as p ∨ ¬p, which is known as the "law of the excluded middle."

Examples

Below are some examples of contradictions in natural language and logical language, along with their truth tables.

Example 1

The following statements in natural language are contradictory:

• "The number 2 is even and odd."
• "It is daytime, but it is nighttime."
• "I am hungry and I am not hungry."
• "The box is open and closed."
• "John is asleep and awake."

All these examples correspond to the proposition p ∧ ¬p, whose truth table is shown above.

Example 2

The proposition p ↔ ¬p is a contradiction; here is its truth table:

p	¬p	p ↔ ¬p
T	F	F
F	T	F

Example 3

The proposition (p ∨ q) ∧ ¬(p ∨ q) is contradictory:

p	q	p ∨ q	¬(p ∨ q)	(p ∨ q) ∧ ¬(p ∨ q)
T	T	T	F	F
T	F	T	F	F
F	T	T	F	F
F	F	F	T	F

Example 4

The compound proposition ¬(p ∧ q → p) is a contradiction.

p	q	p ∧ q	p ∧ q → p	¬(p ∧ q → p)
T	T	T	T	F
T	F	F	T	F
F	T	F	T	F
F	F	F	T	F

More examples

• (p ∧ q) ∧ (r ∧¬p)
• ¬(p ∨ ¬p)
• Negating any logical law leads to a contradiction.

Proofs by Contradiction

Contradictions also play an important role in mathematical proofs. Proofs by contradiction, also called reductio ad absurdum, consist of assuming the opposite of what is to be proven and showing that this assumption leads to a logical contradiction. Upon reaching this contradiction, it is deduced that the original proposition must be true.

In other words, one assumes the proposition is false and, from this assumption, deduces a series of logical consequences that ultimately lead to a contradiction with a known fact or another already proven proposition. By reaching this contradiction, the initial assumption that the proposition was false is refuted, implying that it must be true.

Example: We want to prove that the sum of two even numbers is another even number.

To begin, let's assume this statement is false, meaning: the sum of two even numbers is not an even number, but an odd one. Recall that an even number is one that can be expressed as 2k, where k is an integer.

Let's define two even numbers, a and b. As stated before, a = 2m and b = 2n, where m and n are integers. We proceed to add a and b:

a+b = 2m+2n

Factoring out 2:

a+b = 2(m+n)

Now, m+n is an integer, as it is the sum of two integers. Therefore, the expression 2(m+n) is an even number, and since a+b=2(m+n), it follows that a+b is an even number. This contradicts our initial assumption that a+b is an odd number. 

Since our initial assumption leads to a contradiction, we must conclude that this assumption is false. Therefore, the original statement is true: the sum of two even numbers is even.

Bibliography

• Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
• Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
• Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
• Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
• Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
• Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
• Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.