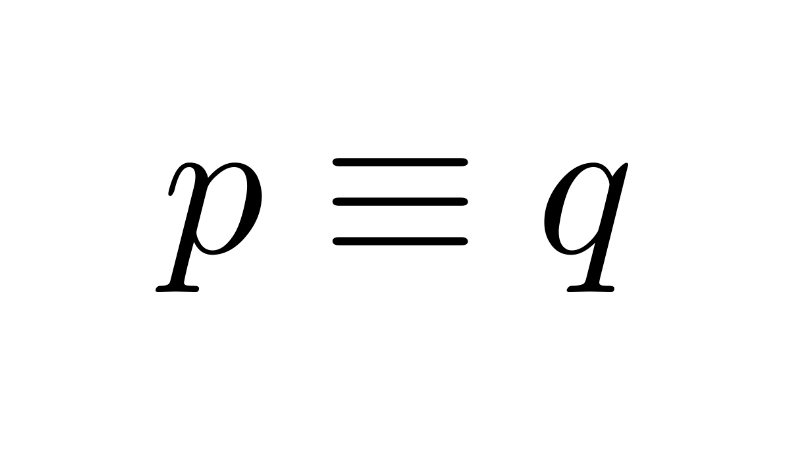
Propositional Logic
Propositional logic, also known as sentential logic or propositional calculus, is a branch of mathematical logic that studies propositions and their combinations through logical connectives.
Unlike predicate logic, propositional logic does not quantify over variables or use free variables, and is therefore considered a foundational logic system. Propositional logic allows for the analysis of the structure and validity of arguments, providing tools to evaluate whether a line of reasoning is correct based on the truth value of its propositions.
In this article, we will cover the basic concepts of propositional logic, including:
- Propositions: statements that can be evaluated as true or false.
- Logical connectives: words or symbols used to connect two or more simple propositions to form compound propositions.
- Truth tables: tools used to evaluate the truth value of compound propositions.
Table of Contents
Propositions
A proposition is a declarative statement that can be either true or false, but not both simultaneously. Propositions are the basic units of propositional logic and are represented by lowercase letters such as p, q, r, s, etc.
Examples:
- p: “The Sun is a star.” (True proposition).
- q: “The Earth is flat.” (False proposition).
- r: “2 + 2 = 4.” (True proposition).
- s: “Water boils at 90°C.” (This proposition is false).
The truth value of a proposition is one of two possible options: true (V) or false (F). It determines whether the information expressed in the proposition is correct or incorrect in relation to reality.
There are two types of propositions:
- Simple or atomic propositions: these are the basic units, like the ones in the previous examples. They cannot be broken down into smaller propositions.
- Compound or molecular propositions: these are formed by combining simple propositions with logical connectives (which we will see next).
Logical Connectives
Logical connectives are words that allow us to connect two or more propositions to form a new proposition with its own truth value. The six most commonly used logical connectives are:
- Negation (¬): represents the falsehood of a proposition and is read as "not" or "it is false that." Example: if p is “the door is open,” then ¬p is “the door is not open.”
- Conjunction (∧): indicates the joining of two or more propositions that must be true simultaneously for the entire expression to be true. It is read as "and" or “but.” Example: if p is “the door is open” and q is “the light is on,” the proposition p ∧ q is “the door is open and the light is on.”
- Disjunction (∨): represents an alternative between two or more propositions. At least one of them must be true for the entire expression to be true. It is read as "or." Example: if p is “the door is open” and q is “the light is on,” p∨q is “the door is open or the light is on, or both.”
- Exclusive disjunction (⊻): represents an alternative between two or more propositions, but only one of them can be true for the expression to be true. It is read as “either ... or ... but not both.” Example: if p is “the door is open” and q is “the light is on,” p⊻q is “either the door is open or the light is on, but not both.”
- Conditional or implication (→): establishes a cause-and-effect relationship between two propositions. The first proposition (antecedent) implies the second (consequent). It is read as "if... then." Example: if p is “the door is open” and q is “the light is on,” p→q is “if the door is open, then the light is on.”
- Biconditional or double implication (↔): expresses a logical equivalence between two propositions. Both propositions must be true or false at the same time. It is read as "if and only if." Example: if p is “the door is open” and q is “the light is on,” p↔q is “the door is open if and only if the light is on.”
Truth Tables
Truth tables are fundamental tools for evaluating the truth value of compound propositions. In them, all possible combinations of truth values for the atomic propositions (also called “interpretations”) are listed, and the truth value of the compound proposition is calculated for each case.
Example: the truth table for the proposition p ∧ q is
| p | q | p ∧ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
The table indicates, in its last column, that the proposition p ∧ q is true when p and q are both true simultaneously, and false in all other cases.
Recommended content:
Propositional Logic Symbology
The following table shows the symbols of propositional logic along with their names and how they are read.
| Symbol | Name | Read as |
|---|---|---|
| ¬ | Negation | not |
| ∧ | Conjunction | and |
| ∨ | Disjunction | or |
| ⊻ | Exclusive disjunction | either... or (but not both) |
| → | Conditional | if... then |
| ↔ | Biconditional | if and only if |
| ∴ | Therefore | therefore |
Logical Equivalences
In propositional logic, two propositions are logically equivalent if they have the same truth value in all possible interpretations. This means that the propositions in question are interchangeable without affecting the validity of an argument.
Two propositions p and q are considered logical equivalences (symbolized as p ≡ q or p ↔ q) if and only if their truth tables match in every row. That is, for every possible combination of truth values of the atomic propositions that make up p and q, the truth value of p must be the same as the truth value of q.
Logical equivalences are essential in mathematical logic and computer science because they allow for the simplification of complex propositions and the proof of theorems, as well as enabling the transformation of arguments from one form to another without altering their validity.
Some of the most important laws of logical equivalence are:
- Double Negation Law: ¬(¬p) ≡ p.
- Commutative Law for Conjunction: p ∧ q ≡ q ∧ p.
- Associative Law for Conjunction: (p ∧ q) ∧ r ≡ p ∧ (q ∧ r).
- Distributive Law of Conjunction over Disjunction: p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r).
- Commutative Law for Disjunction: p ∨ q ≡ q ∨ p.
- Associative Law for Disjunction: (p ∨ q) ∨ r ≡ p ∨ (q ∨ r).
- Absorption Law: p ∧ (p ∨ q) ≡ p.
- Absorption Law: p ∨ (p ∧ q) ≡ p.
- De Morgan's Law: ¬(p ∧ q) ≡ ¬p ∨ ¬q
- De Morgan's Law: ¬(p ∨ q) ≡ ¬p ∧ ¬q
To check the logical equivalence of two propositions, one can construct truth tables. There, all possible combinations of truth values for the component propositions are evaluated and the results are compared.
Properties of logical equivalences:
- Reflexivity: every proposition is equivalent to itself (p ≡ p).
- Symmetry: if p ≡ q, then q ≡ p.
- Transitivity: if p ≡ q and q ≡ r, then p ≡ r.
Rules of Inference
Rules of inference are patterns or formulas that allow for the deduction of a new, valid proposition from one or more propositions (premises) that are assumed to be true. These rules are fundamental for constructing valid logical arguments and reasoning rigorously.
Some of the most common rules of inference are:
1) Modus Ponens (MP): allows us to conclude that a proposition is true if we know that an implication is true and its antecedent is also true. In symbols: if p → q and p are true, then q must be true.
*\begin{array}{l} p → q \\ p \\ \hline \therefore p \end{array}*
Example:
- If John studies (p), then he will pass the exam (q).
- John studies (p).
- Therefore, John will pass the exam (q).
2) Modus Tollens (MT): allows us to conclude that the antecedent of an implication is false if we know the implication is true and its consequent is false. In symbols: if p → q is true and q is false, then p must be false.
*\begin{array}{l} p → q \\ ¬q \\ \hline \therefore ¬p \end{array}*
Example:
- If it rains (p), then the street is wet (q).
- The street is not wet (¬q).
- Therefore, it is not raining (¬p).
3) Disjunctive Syllogism (DS): allows us to conclude that one of two propositions is true if we know that a disjunction is true and one of its parts is false. In symbols: if p ∨ q is true and p is false, then q must be true.
*\begin{array}{l} p ∨ q \\ ¬p \\ \hline \therefore q \end{array}*
Example:
- Mary is at home (p) or she is at the office (q).
- Mary is not at home (¬p).
- Therefore, Mary is at the office (q).
4) Hypothetical Syllogism (HS): allows us to conclude a new implication from two connected implications. In symbols: if p → q is true and q → r is true, then p → r must be true.
*\begin{array}{r} p → q \\ q → r \\ \hline \therefore p → r \end{array}*
Example:
- If Peter goes to the movies (p), then he will buy popcorn (q).
- If Peter buys popcorn (q), then he will be happy (r).
- Therefore, if Peter goes to the movies (p), then he will be happy (r).
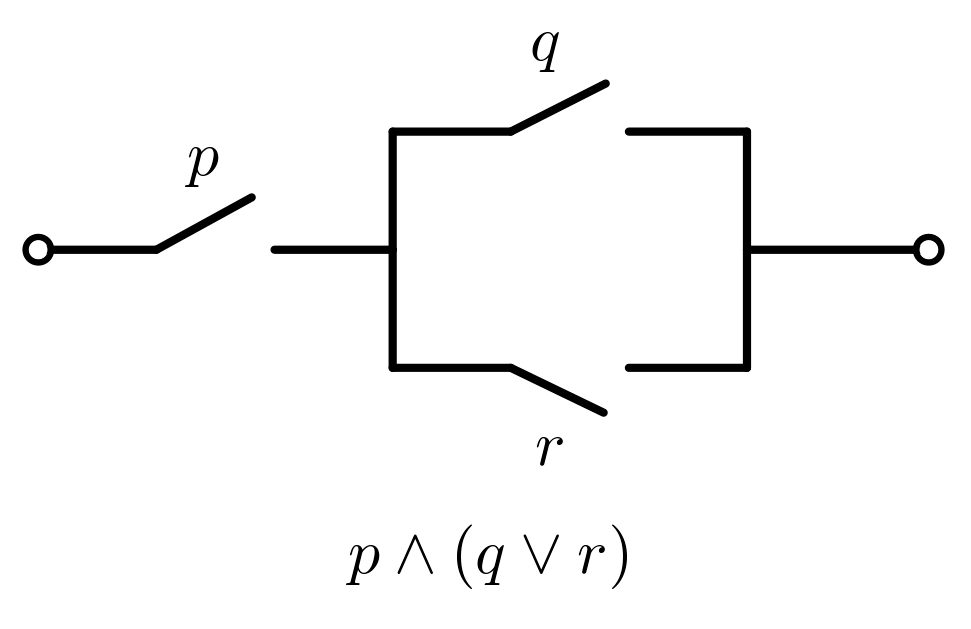
Logic Circuits
Logic circuits are graphical representations that use symbols and diagrams to illustrate the relationships between propositions and their truth values. These circuits provide an intuitive way to visualize the operation of logical connectives and how truth values are determined, associating them with the flow of current in an electrical circuit with one or more switches.
In digital electronics, these circuits process binary signals (0 and 1, representing false and true respectively) to perform logical operations. Logic circuits are fundamental to the construction of digital systems such as computers, mobile devices, and other electronic equipment.
The basic components of a logic circuit are:
1) Propositions (logic variables): represent the inputs to the circuit. Each logic variable can take one of two values: 0 (false) or 1 (true).
2) Logical connectives (logic gates): perform logical operations on the variables. The basic logic gates are:
- AND: produces an output of 1 only if all its inputs are 1.
- OR: produces an output of 1 if at least one of its inputs is 1.
- NOT: produces an output that is the inverse of its input (0 becomes 1, and 1 becomes 0).
- NAND (negation of conjunction): produces an output of 0 only if all its inputs are 1.
- NOR (negation of disjunction): produces an output of 0 if at least one of its inputs is 1.
- XOR (exclusive disjunction): produces an output of 1 if one and only one of its inputs is 1.
- XNOR (negation of exclusive disjunction): produces an output of 1 if both inputs are the same.
Example: the logic circuit associated with the compound proposition p ∧ (q ∨ r) is:
Applications of Propositional Logic
Propositional logic has numerous applications in various fields due to its ability to formalize and analyze arguments. Some of the main applications of propositional logic include:
- Digital circuits: They are the foundation of computers and other electronic devices and are based on Boolean algebra, which is a direct application of propositional logic.
- Mathematics: Propositional logic is fundamental to the axiomatization and development of mathematics. It is used to define mathematical concepts, and to formulate and prove theorems.
- Computer Science: Programming languages are based on principles of propositional logic to evaluate conditions and control program flow.
- Philosophy: In philosophical analysis, propositional logic is used to study the nature of truth, meaning, and argumentation.
- Law: Propositional logic is used in legal analysis to evaluate the validity of legal arguments and to identify potential fallacies in legal reasoning.
- Education: Teaching propositional logic in primary and secondary education helps develop students' critical thinking and logical reasoning skills.
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

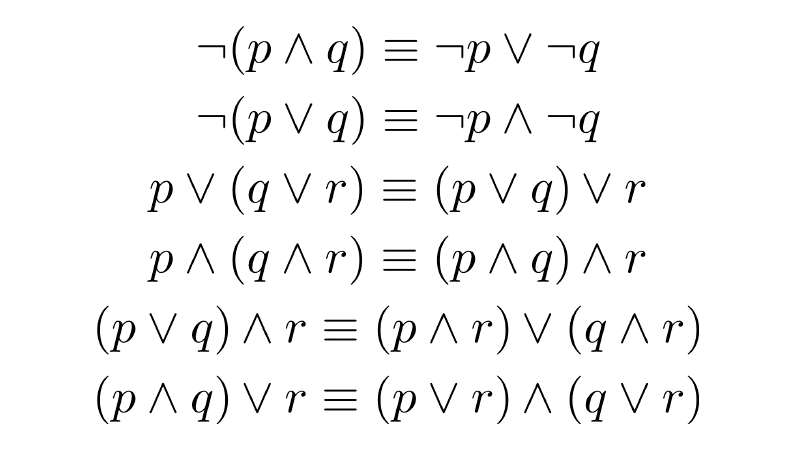
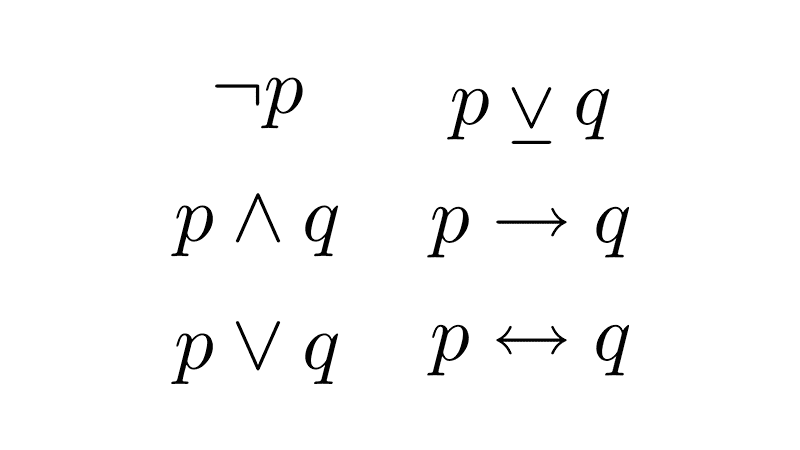
Related posts