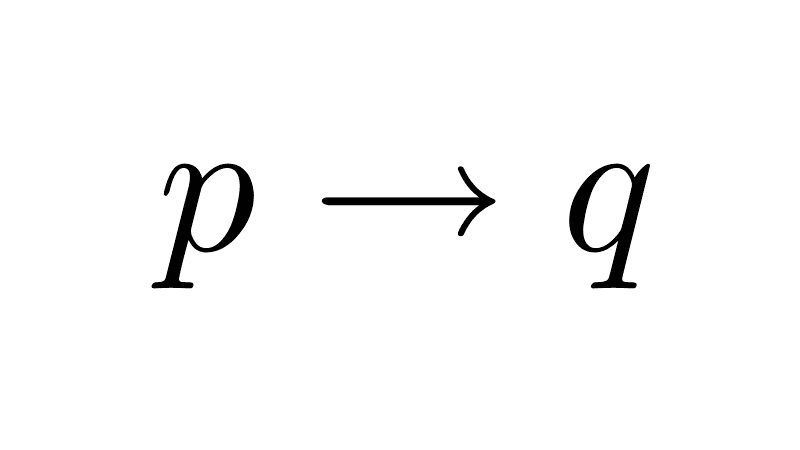
Logical Biconditional
The biconditional, also known as double implication, is a logical connective that links two propositions to form a new one which is true when the original propositions have the same truth value (both true or both false), and is false otherwise. It is represented by the symbols “↔” or “⇔” and is read as “if and only if”.
Some examples of the use of the biconditional are:
- "A triangle is equilateral if and only if its three internal angles are equal". This compound proposition is true because both conditions, having equal sides and equal angles, are equivalent in a triangle.
- In the expression “I will pass if and only if I study for the exam", the biconditional establishes a dual condition: studying is necessary and sufficient to pass, and passing implies that I have studied. If I study and pass, it is true; if I don't study and pass anyway, it is false (just as if I study and don't pass).
- "You can enter the concert if and only if you have a ticket" is true only in two cases: if you have a ticket and can enter, or if you don't have a ticket and cannot enter. The sentence becomes false if, for example, you have a ticket but are not allowed to enter.
Table of Contents
Truth table
As we mentioned, the biconditional is true only when the two propositions it connects have the same truth value (both true or both false), and it is false when the truth values are different (one true and one false). This becomes clear when analyzing its truth table:
| p | q | p ↔ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
There are different ways to read the biconditional proposition p ↔ q, all of them equivalent in meaning. Some of the most common are:
- p if and only if q.
- p is equivalent to q.
- p is a necessary and sufficient condition for q.
- If p, then q, and if q, then p.
- q if and only if p.
In abbreviated form, the expression "if and only if" is often written as "iff". Likewise, the logical equivalence symbol (≡) is synonymous with the biconditional (↔) and is frequently used to indicate that two propositions are logically equivalent.
It is important not to confuse the biconditional (↔) with the simple conditional (→). While the conditional establishes that one proposition is a sufficient condition for the other (if p, then q), the biconditional asserts a mutual relationship of necessity and sufficiency: p is a necessary and sufficient condition for q, and vice versa.
For example, the proposition "if a number is divisible by 4, then it is even" is a true conditional: being divisible by 4 is a sufficient condition for being even. If we try to convert it into a biconditional: "a number is divisible by 4 if and only if it is even," the proposition becomes false. The reason is that the biconditional requires that the condition also work in reverse.
In this case, it is not true that "if a number is even, then it is divisible by 4" (think of the number 6, which is even but not divisible by 4). Therefore, being even is not a sufficient condition for being divisible by 4, which breaks the equivalence required by the biconditional.
Properties
The biconditional has a series of fundamental logical properties that we will see below.
1) Equivalence to a conjunction of conditionals: the essential property of the biconditional is that it is logically equivalent to the conjunction of two conditionals directed in opposite senses (a conditional and its reciprocal).
p ↔ q ≡ (p → q) ∧ (q → p)
This means that stating "p if and only if q" is the same as stating "if p, then q" and "if q, then p" simultaneously.
2) Definition with conjunction and disjunction: the double implication can also be defined using the connectives of conjunction and disjunction.
p ↔ q ≡ (p ∧ q) ∨ (¬p ∧ ¬q)
Note that it is equivalent to stating that both propositions are true or that both are false.
3) Identity property: every proposition is equivalent to itself; this is a fundamental property.
p ↔ p
4) Commutative property: the order of the propositions in a biconditional does not alter its truth value.
p ↔ q ≡ q ↔ p
5) Transitive property: if a proposition is equivalent to a second, and this second is equivalent to a third, then the first and the third are also equivalent.
If (p ↔ q) and (q ↔ r) are true, then (p ↔ r) is also true.
6) Associative property: when multiple biconditionals are linked, the way they are grouped does not change the result.
(p ↔ q) ↔ r ≡ p ↔ (q ↔ r)
7) Relation to exclusive disjunction: the biconditional and the exclusive disjunction (⊻) are logical negations of each other. While the biconditional is true when the values match, the exclusive disjunction is true when the values are different.
(p ↔ q) ≡ ¬(p ⊻ q)
8) Negation of a biconditional: negating an equivalence means stating that the propositions have different truth values; this is precisely the definition of exclusive disjunction.
¬(p ↔ q) ≡ (p ⊻ q) ≡ (p ∧ ¬q) ∨ (¬p ∧ q)
9) Contraposition of the biconditional: just as with the simple conditional, the double implication has a valid contrapositive form.
(p ↔ q) ≡ (¬q ↔ ¬p)
Leave a Reply

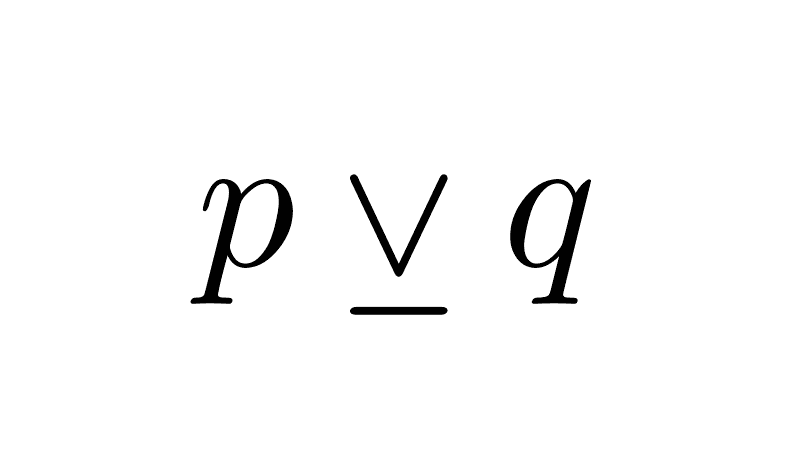
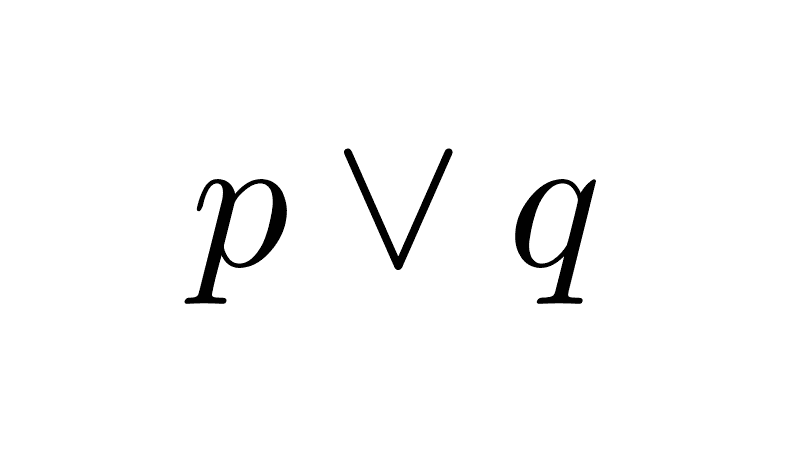

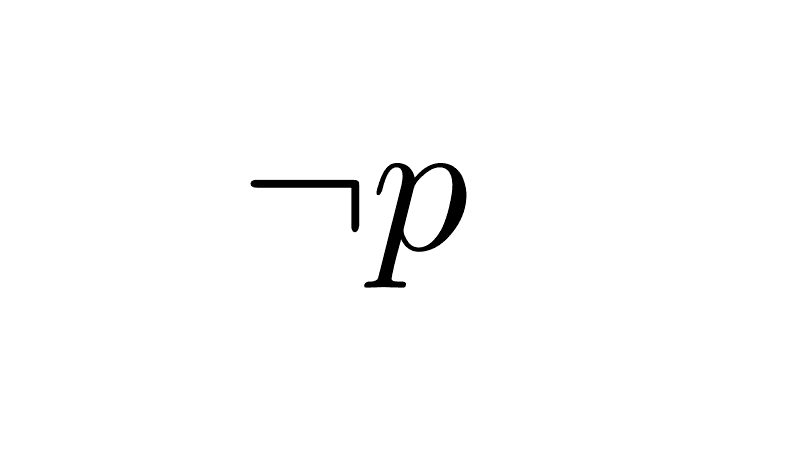
Related posts