
Logical Quantifiers
Logical quantifiers are symbols used in mathematical logic to specify the quantity of elements in a set that satisfy a certain property or predicate. They transform propositional functions (open statements with variables) into complete propositions with a defined truth value.
A propositional function, such as P(x): "x is prime", is not a proposition because its truth value depends on the value of x. Quantifiers allow it to be converted into a proposition by specifying how many elements of the domain satisfy the property.
Table of Contents
Types of Quantifiers
The two most commonly used quantifiers are the universal and the existential. There is also a special case of the latter known as the unique existential quantifier.
Universal Quantifier (∀)
The universal quantifier is used to assert that a property holds for all elements of a set or domain, without exception. Its symbol is ∀ (an inverted "A," from the German word Allgemein, meaning "for all" or "general"). It is usually read as "for all," "for each," "every," or "always."
The general form is ∀x : P(x), where P(x) is a propositional function, and it is interpreted as: "for all x, P(x) is true" or “for all x, P(x) holds.”
The universe of discourse (or domain) is the set of elements over which the quantification applies. Defining it is essential, as the meaning of a proposition depends entirely on it. If we have a universe of discourse U, we can include it directly in the quantified statement: ∀x ∈ U : P(x).
A universally quantified proposition is true if all elements of the universe of discourse satisfy the specified condition. If there is at least one element that does not satisfy it, the statement is false.
This quantifier allows for the creation of phrases like “all humans are mortal,” “all plants are living beings,” “all Argentinians are Latin Americans,” etc. We will now look at examples applied to mathematics.
Examples
- ∀x ∈ N : x > 0 states that “for every natural number x, it holds that x is greater than zero.” This is true.
- ∀x ∈ R : x ≥ 1 asserts that every real number is greater than or equal to 1; this is false, because there are real numbers less than 1.
- ∀x ∈ R : x2 ≥ 0 states that the square of every real number is greater than or equal to zero. This is a true proposition, as the square of any real number is always a non-negative number.
- “∀x ∈ Z : 2x is even” asserts that for every integer, its double is even. This is a true proposition, as any integer multiplied by 2 results in an even number by definition.
- ∀x ∈ R : sin2(x) + cos2(x) = 1 means that for every real number, the fundamental trigonometric identity holds. This is a true proposition.
- ∀n ∈ N : n + 1 > n tells us that adding 1 to any natural number always results in a number greater than the original. This is true.
Existential Quantifier (∃)
The existential quantifier is used to express that there is at least one element in the universe of discourse that satisfies a certain property or predicate. Its symbol is ∃, which comes from the inverted letter "E" of the English word exists. It is usually read as "there exists," "there is at least one," or "there exists at least one element such that...".
The general form of this quantifier is written as: ∃x | P(x) and it means that there is some value of x within the considered universe that makes the proposition P(x) true.
A proposition containing the quantifier ∃ is true if at least one element can be found in the universe of discourse that satisfies the specified condition. It does not matter if several elements or even all of them satisfy it; the existence of one is sufficient.
This quantifier allows for the creation of phrases like “there are young people,” “there is wooden furniture,” “there are orange cats,” etc. Next, we will see examples applied to mathematics.
Examples
- ∃x ∈ R | x2 = 4 means “there exists a real number whose square is 4.” This is true: 2 is an example, as is -2.
- “∃n ∈ N / n is even and prime” tells us that there exists at least one natural number that is both even and prime. Again, this is true: 2 is a case (in fact, the only one).
- ∃x ∈ Z | x + 5 = 0 expresses that there exists an integer which, when added to 5, gives 0. This is true, as -5 is that number.
- ∃y ∈ Q / y2 = 2 states that there exists a rational number whose square is 2. This proposition is false, as √2 is irrational.
- ∃x ∈ R | x3 = 27 asserts that there exists a real number whose cube is 27. In this case, x = 3, so the proposition is true.
- ∃x ∈ R / x2 = -1 expresses that there exists a real number that, when squared, results in -1. This proposition is false, because every real number squared is non-negative. If the universe of discourse were the set of complex numbers (C), it would be a true proposition.
Uniqueness Quantifier (∃!)
The uniqueness quantifier, also called the unique existential quantifier, is used to assert that there is exactly one element in the universe of discourse that satisfies a certain condition. Its usual symbol is ∃!, which is read as "there exists a unique," "there exists exactly one," or "there is only one."
The general form is: ∃! x | P(x) , which means that within the universe of discourse, there is only one value of x that makes the proposition P(x) true.
A proposition with ∃! will be true only if two conditions are met:
- There exists at least one element that satisfies the property.
- That element is unique, meaning there are not two or more that satisfy it.
Examples
- ∃! n ∈ N | n is even and prime means "there exists a unique natural number that is even and prime." This is true, because only the number 2 meets this condition.
- ∃! x ∈ R | x2 = 4 asserts that "there exists a unique real number whose square is 4." This is false, as both 2 and -2 satisfy the condition, so it is not unique.
- ∃! n ∈ N | n > 1000 means "there exists a unique natural number greater than 1000." This is false, because there are infinitely many natural numbers greater than 1000.
- ∃! n ∈ N | n = 7 states "there exists a unique natural number that is equal to 7." This is true, because only the number 7 satisfies the proposition.
- ∃! x ∈ Z | x + 5 = 0 states "there exists a unique integer which, when added to 5, equals 0." This is true, because only x = -5 satisfies the condition.
- ∃! y ∈ Q | y2 = 2 asserts that "there exists a unique rational number whose square is 2." This is false, because in reality, no such rational number exists.
Quantifiers apply to the closest propositional function, unless modified by grouping symbols (parentheses, brackets, braces). For example: ∀x: P(x) ∨ Q(x) is interpreted as [∀x: P(x)] ∨ Q(x). If we wanted the quantifier to apply to both functions, we would write ∀x: [ P(x) ∨ Q(x) ].
Negation of Quantifiers
Negating a quantified statement means inverting the quantifier and, at the same time, negating the predicate. This principle applies to the universal quantifier (∀) and the existential quantifier (∃). The uniqueness quantifier (∃!) is considered a special case of the existential, so its negation is handled derivatively, not directly.
Negation of the Universal Quantifier
¬[∀x : P(x)] ≡ ∃x | ¬P(x)
That is: “it is not true that all x satisfy P(x)” is equivalent to “there exists at least one x that does not satisfy P(x).”
Intuitively, saying “it is not true that all swans are white” is logically equivalent to saying “there exists at least one swan that is not white.” A single counterexample is enough to refute a universal claim.
Examples
1) ¬(∀x ∈ R | x2 > 0) ≡ ∃x ∈ R | ¬(x2 > 0)
Here, "it is not true that for every real number its square is greater than 0" is equivalent to saying "there exists at least one real number whose square is not greater than 0." This is true, as x = 0 is a counterexample (02 = 0 is not greater than 0). Knowing this, we could write: ∃x ∈ R | x2 = 0.
2) ¬(∀n ∈ N | n is prime) ≡ ∃n ∈ N | ¬(n is prime) ≡ ∃n ∈ N | n is not prime
In this case, "it is not true that all natural numbers are prime" is equivalent to "there exists at least one natural number that is not prime." This is true, for example, n = 4 is not prime.
3) ¬(∀x ∈ Z | x2 is odd) ≡ ∃x ∈ Z | x2 is even
In this example, "it is not true that the square of every integer is odd" is equivalent to asserting that "there exists at least one integer whose square is not odd." This is true, as x = 2 satisfies it (22 = 4, which is even).
Negation of the Existential Quantifier
¬[∃x | P(x)] ≡ ∀x : ¬P(x)
That is: “it is not true that there exists some x that satisfies P(x)” is equivalent to “all x do not satisfy P(x).”
In everyday language, saying “it is not true that there are fire-breathing dragons” is the same as stating “all dragons do not breathe fire,” or more simply, “no dragon breathes fire.”
Examples
1) ¬(∃n ∈ N | n < 0) ≡ ∀n ∈ N | ¬(n < 0)
In this case, we see that "it is not true that there exists a natural number less than 0" is equivalent to "all natural numbers are not less than 0." This is true, because natural numbers start at 1 (or 0, depending on the convention) and none are negative.
2) ¬(∃x ∈ Q | x2 = 2) ≡ ∀x ∈ Q | x2 ≠ 2
Here, "it is not true that there exists a rational number whose square is 2" is equivalent to "for every rational number, its square is not 2." This is true, because √2 is not rational.
3) ¬(∃x ∈ R | x2 = -1) ≡ ∀x ∈ R | x2 ≠ -1
In this case, "it is not true that there exists a real number whose square is -1" is equivalent to saying "for every real number, its square is not -1." This is true, because no real number satisfies x2 = -1.
The cases of negation are summarized in the following table.
| Case | How it's done | Symbolism |
|---|---|---|
| Negation of the universal quantifier | It is changed to an existential quantifier, and the predicate is negated | ¬[∀x : P(x)] ≡ ∃x | ¬P(x) |
| Negation of the existential quantifier | It is changed to a universal quantifier, and the predicate is negated | ¬[∃x | P(x)] ≡ ∀x : ¬P(x) |
Combining Quantifiers
Multiple quantifiers, including combinations of existential (∃) and universal (∀) quantifiers, can appear in a single logical proposition. When the quantifiers are of the same type (all ∀ or all ∃), the order does not change the meaning. However, when the quantifiers are mixed (∃ and ∀), the order does matter and can change the meaning of the proposition.
To illustrate this, let's consider a generic predicate P(x, y). The four main schemes are:
1) ∀x ∀y : P(x, y) which is read as “for all x and for all y, P(x, y) holds."
For example, the commutative property of addition and multiplication for real numbers is expressed as:
∀x ∈ R ∀y ∈ R : x + y = y + x
∀x ∈ R ∀y ∈ R : x · y = y · x
2) ∃x ∃y | P(x, y) is read as "there exist an x and a y that satisfy P(x, y)”.
An example is: ∃x ∈ Z ∃y ∈ Z | x2 + y2 = 25. This is true, because x = 3, y = 4 satisfy the equation.
3) ∀x ∃y | P(x, y) is read as "for all x there exists a y that satisfies P(x, y)".
For example: ∀x ∈ R ∃y ∈ R | x + y = 0. This is true, because for any real number x, there always exists a y = -x that cancels it out in addition (the opposite).
4) ∃x ∀y : P(x, y) is read as "there exists an x such that for all y, P(x, y) holds"
Example: ∃x ∈ R ∀y ∈ R : x · y = 0. This is true, because if x = 0, no matter what value y takes, the product is always 0.
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

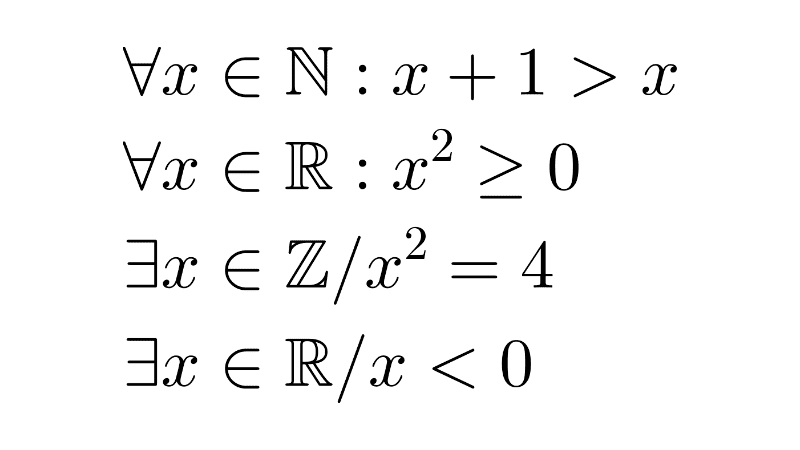
Related posts