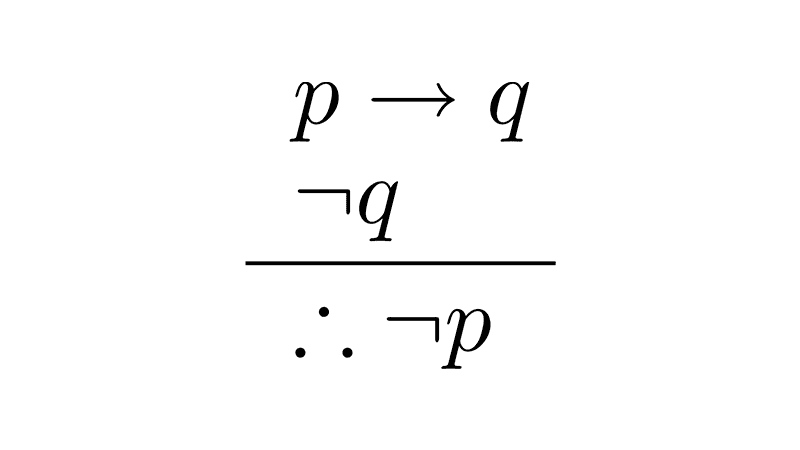
Mathematical Logic
Mathematical logic is a discipline that focuses on the study and formalization of reasoning and thought using a specific set of rules and symbols. Its main objective is to provide a rigorous and precise framework for expressing ideas, arguments, and relationships within the field of mathematics.
When we express an idea in natural language, there can be multiple possible interpretations. In mathematics, where precision is essential, an ambiguous or poorly formulated expression can lead to erroneous conclusions. Mathematical logic introduces a set of formal symbols and rules that eliminate ambiguity and allow statements and relationships to be expressed clearly and precisely.
The symbolism of mathematical logic is universal, which facilitates communication among mathematicians from different cultures and allows mathematical ideas to be accessible to everyone, regardless of their native language.
In mathematics, it is necessary to prove the validity of statements and theorems. Logic provides precise rules for constructing solid arguments and formal proofs; this ensures that conclusions are correct and reliable.
Table of Contents
Types of Logic
There are several types of mathematical logic used to model different aspects of reasoning and computation. The most common are:
- Model theory: Studies the relationship between the symbols of a formal system and the objects they represent. In other words, it analyzes how abstract mathematical structures can be interpreted in the real world.
- Proof theory: Focuses on the rules and methods for constructing formal proofs of mathematical theorems. It investigates how new truths can be deduced from axioms and inference rules.
- Set theory: Studies the properties of sets, which are collections of objects. It is one of the fundamental pillars of modern mathematics and has applications in various areas such as topology, mathematical analysis, and measure theory.
- Computability theory: Focuses on determining which problems can be solved by computational algorithms and which cannot. By studying the capabilities and limitations of abstract computing machines, such as Turing machines, this discipline addresses fundamental questions about the nature of computation and the complexity of problems.
- Propositional logic: Deals with the study of propositions and how they are combined using logical connectives.
- Predicate logic: Extends propositional logic to include quantifiers such as "for all" (∀) and "there exists" (∃), allowing for the expression of more complex sentences involving individual objects and properties.
- Modal logic: Used to reason about possibility, necessity, and other modal concepts. It introduces modal operators like "possibly" and "necessarily," allowing for the expression of propositions that vary across possible worlds or states.
Propositional Logic
Propositional logic is a branch of logic that focuses on the study of propositions and their logical relationships. It uses connectives and truth tables to analyze and understand how these propositions combine and relate, which allows us to make logical decisions and construct valid arguments. Below, we will explore the basic concepts of propositional logic.
Propositions are statements or declarations that can be either true or false, but not both at the same time. They are denoted by lowercase letters such as p, q, r, s, etc.
Examples:
p: "The sky is blue"
q: "2 + 2 = 4"
r: "3 is an even number"
Propositions can have two possible truth values: true (T) or false (F). There is no other possibility. The truth value of a proposition p is denoted as V(p). In the case of the previous examples:
V(p)=T
V(q)=T
V(r)=F
In mathematical logic, there are symbols used to combine propositions and form new propositions; these are called operators or logical connectives. The most frequently used are:
- Negation (¬): Turns a true proposition into a false one, and vice versa.
- Conjunction (∧): Returns true only if both propositions are true.
- Disjunction (∨): Returns true if at least one of the propositions is true.
- Implication (→): Establishes a conditional relationship, where if the first proposition is true, then the second must also be true.
- Biconditional (↔): Returns true if both propositions have the same truth value.
Examples:
p: "The sky is blue"
q: "2 + 2 = 4"
r: "3 is an even number"
¬p: "The sky is not blue"
q∧r: "2+2=4 and 3 is an even number"
p∨q: "The sky is blue or 2+2=4"
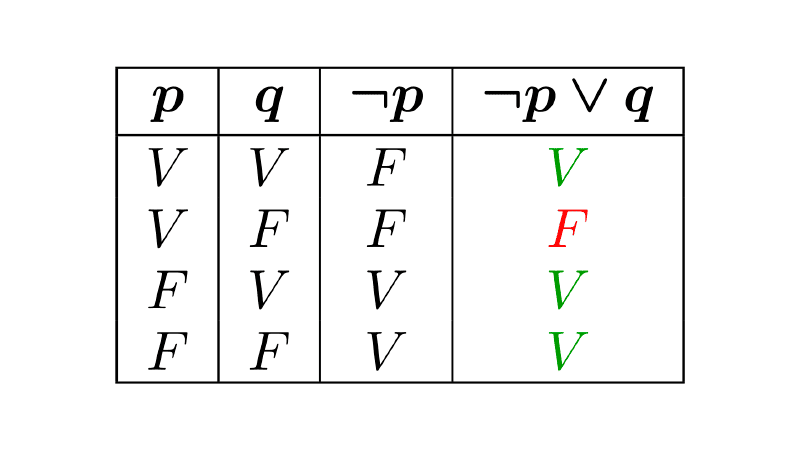
Propositions formed from simpler ones using logical connectives are called compound propositions. To determine the truth value of a compound proposition, we use truth tables. These show all possible truth values for a given proposition based on the truth or falsity of its components and the operators used.
When creating a truth table, we can obtain one of these three cases:
- Tautology: A compound proposition that is always true, regardless of the truth values of its components. Tautologies are also known as logical laws.
- Contingency: A compound proposition that can be either true or false depending on the truth values of its components.
- Contradiction: A compound proposition that is always false, regardless of the truth values of its components.
Predicate Logic
Predicate logic is an extension of propositional logic that allows for expressing more complex relationships and quantifying over objects and properties. It enables the creation of statements like "all natural numbers are positive" or "there exists a prime number greater than 100."
Quantifiers are symbols used to express the quantity of elements that satisfy a proposition. The two most commonly used quantifiers are:
- Universal Quantifier (∀): Used to state that a statement is true for all elements in a given set. For example, "∀x P(x)" means that the proposition P(x) is true for all values of x in the set.
- Existential Quantifier (∃): Used to state that at least one element in a set satisfies a proposition. For example, "∃x Q(x)" means there is at least one element in the set for which the proposition Q(x) is true.
Reasoning
Reasoning or an argument is a sequence of propositions structured in such a way that if the premises are true, the conclusion will also be true. It is a process in which formal rules are used to infer conclusions from premises.
Some examples of reasoning are:
- If it rains, then the ground is wet; but the ground is not wet. Therefore, it is not raining.
- All humans are mammals, and all mammals are vertebrates. Therefore, all humans are vertebrates.
- If I study hard, then I will pass the exam. I studied hard, therefore, I will pass the exam.
The parts of a logical argument are as follows:
- Premises: These are the statements given as the basis for the conclusion.
- Conclusion: This is the final statement reached from the premises.
In example 1, "if it rains, then the ground is wet" and "the ground is not wet" are the premises; the conclusion is "it is not raining."
The most common type of reasoning used in mathematical logic is deductive reasoning, which starts from premises known to be true, and through logical rules, infers a necessary conclusion that logically follows from those premises. If the premises are true and the form of the argument is valid, then the conclusion will necessarily also be true.
Contents
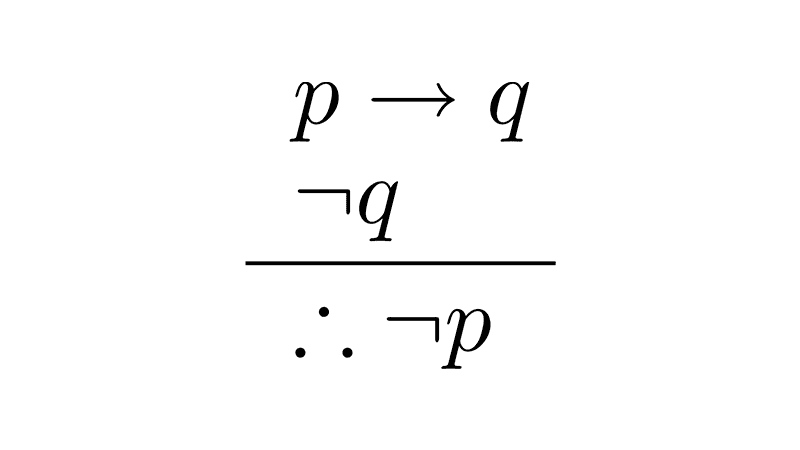
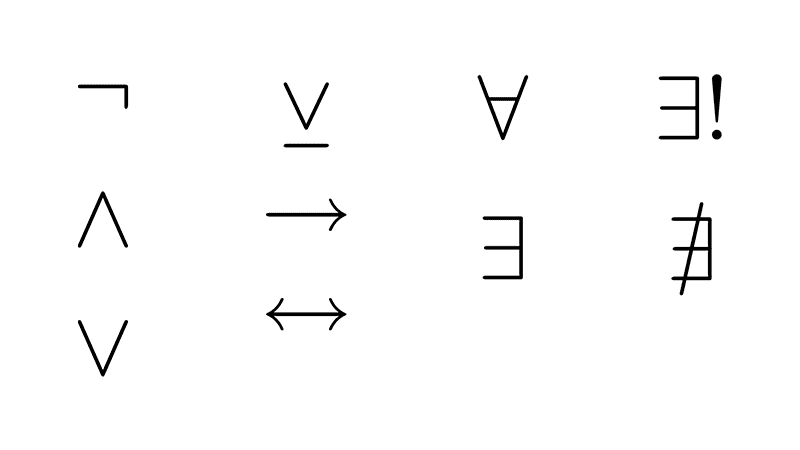
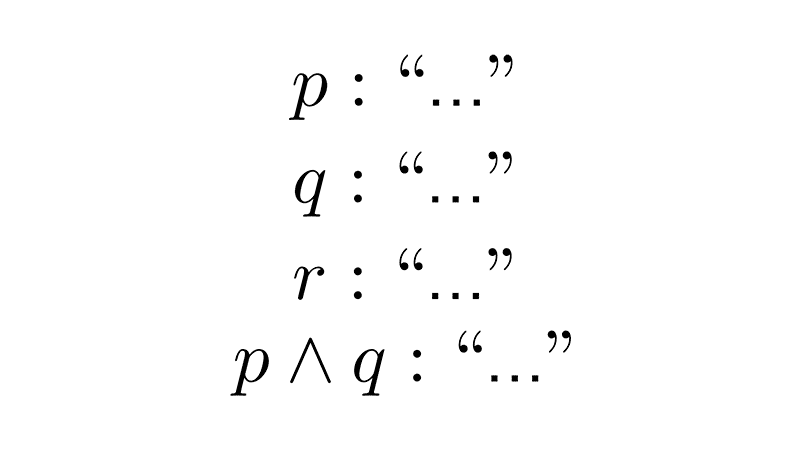
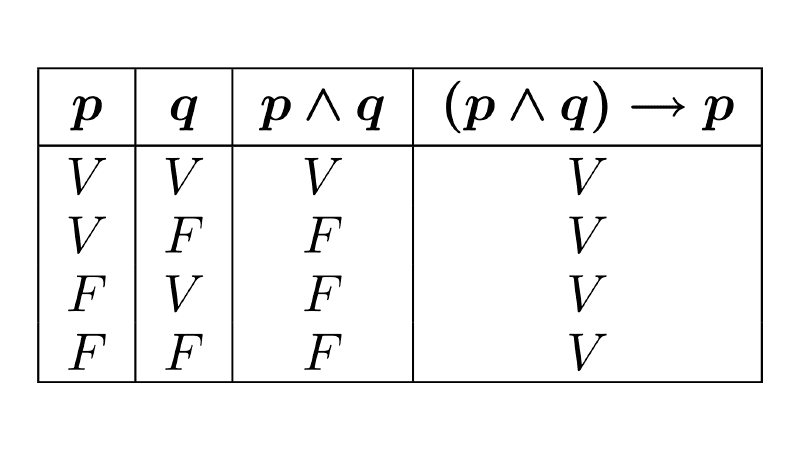
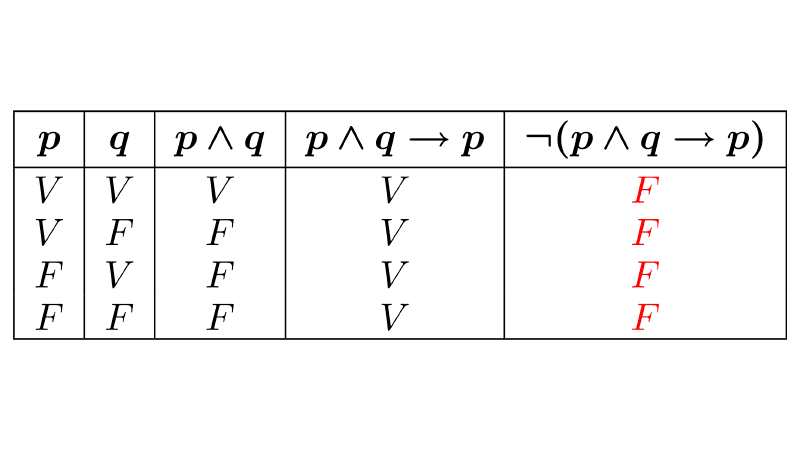
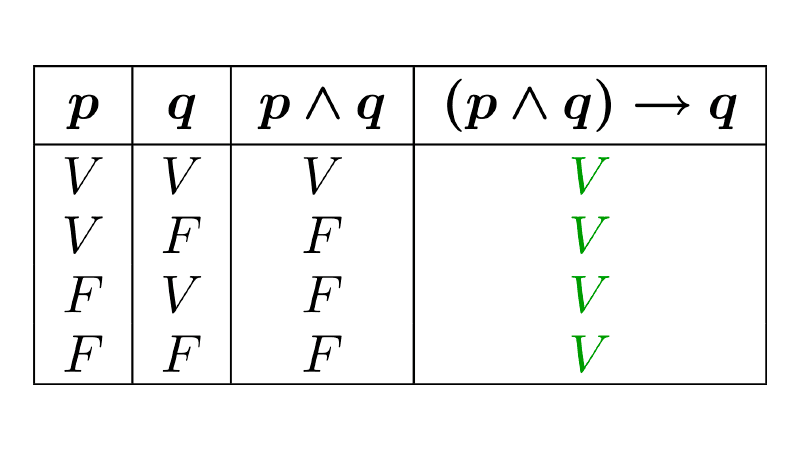
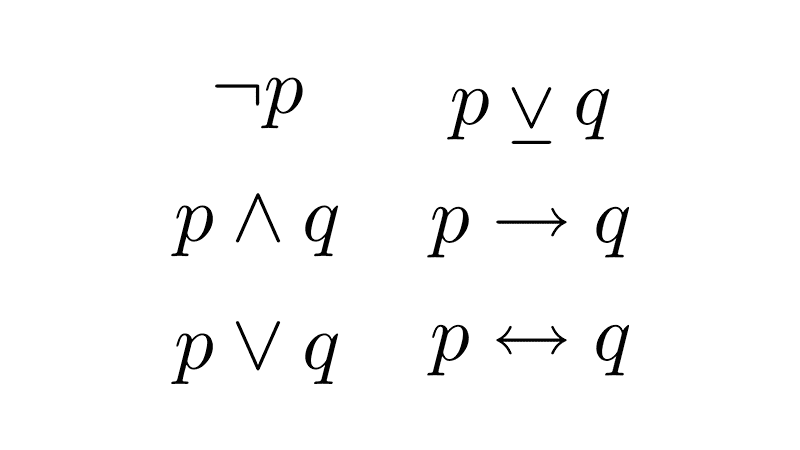
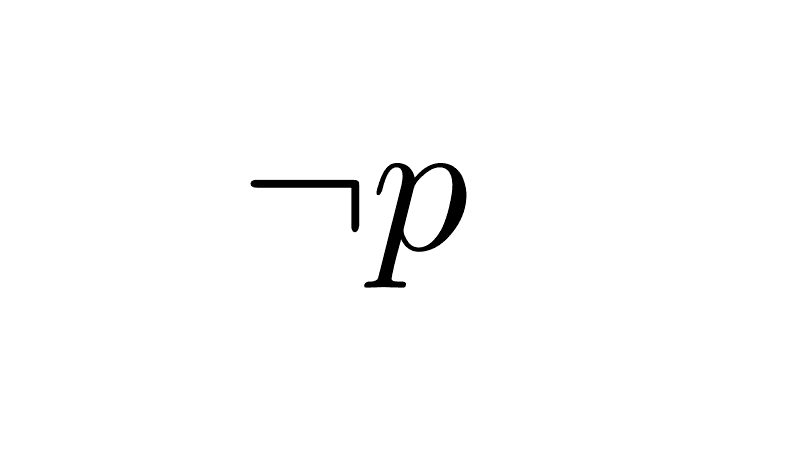

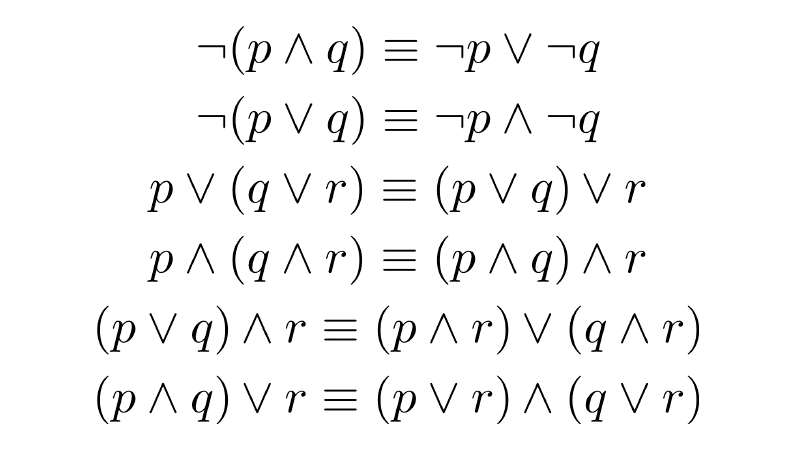
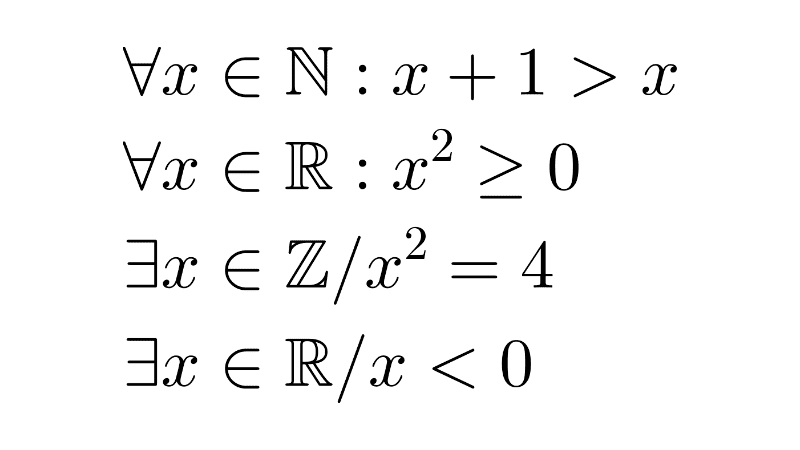
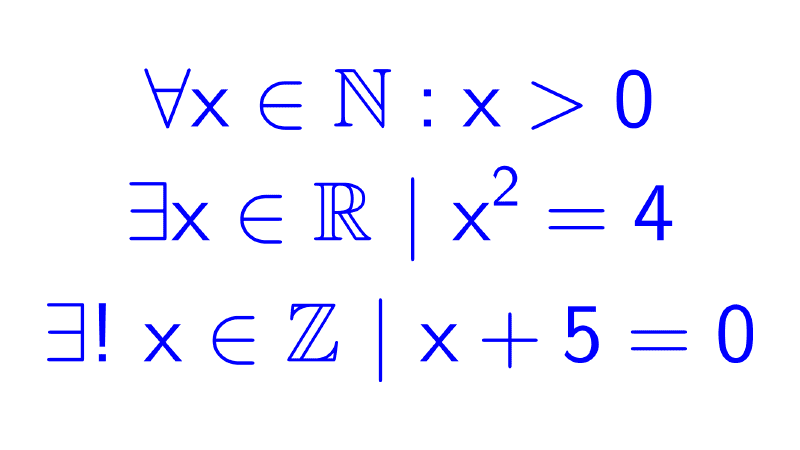
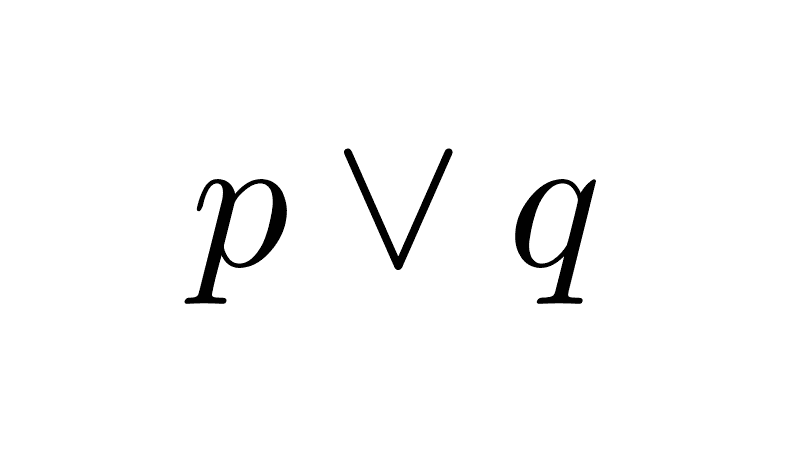
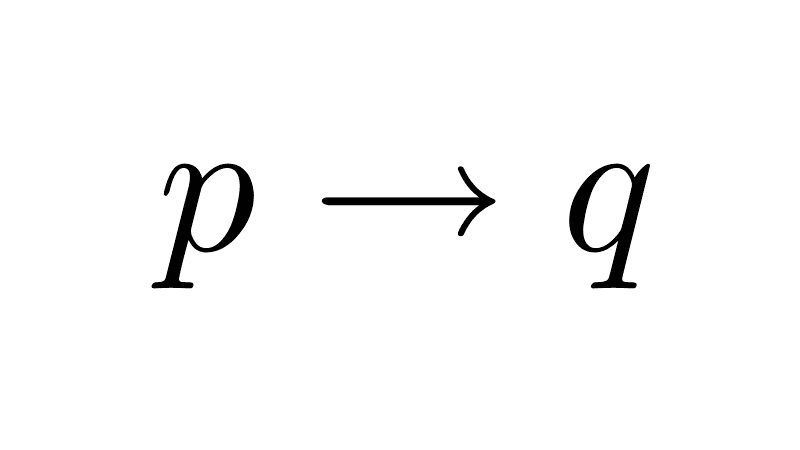

Leave a Reply