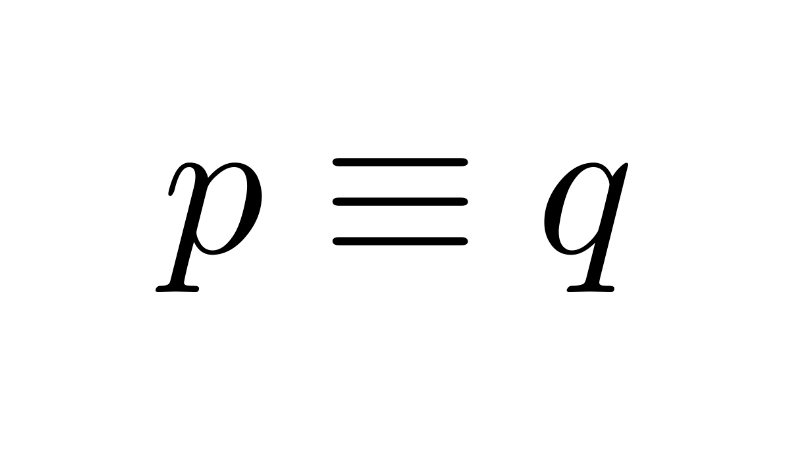
Logical Propositions
Logical propositions are declarative statements that have a complete meaning and can be classified as either true or false, but not both simultaneously. These statements are the fundamental element of logic and must be clear and precise, without ambiguity, so that their truth value can be determined objectively.
For example, “the Earth is a planet” is a proposition whose truth value is true, while “2 + 2 = 5” is a false proposition. However, not all sentences are propositions; phrases like “What time is it?” or “Study more!” cannot be true or false, and therefore, are not propositions.
Table of Contents
Examples
Other examples of propositions are:
- “Jupiter is the largest planet in the Solar System.”
- “The Earth orbits the Sun.”
- “2 is an even number.”
- “The Thames is a major river.”
- “Coffee contains caffeine.”
- “The piano is a musical instrument.”
Examples of sentences that are NOT propositions:
- “Close the door!”
- “What a beautiful day!”
- “How much does this product cost?”
- “Turn left.”
- “I hope it rains tomorrow.”
Similarly, meaningless sentences or those containing undefined variables (such as “x is greater than 3,” without knowing what x is) are not propositions until the value of the variable is specified.
Types of propositions
There are two types of propositions:
- Simple or atomic propositions: are those that cannot be broken down into smaller parts without losing their meaning, express a single idea, and contain no logical connectives. For example, “the Earth revolves around the Sun” is a simple proposition.
- Compound or molecular propositions: are those formed from simple propositions using logical connectives, such as “today is Monday and it is cold,” where the connective “and” (conjunction) joins two statements. Other common connectives include "or" (disjunction), "if... then..." (conditional), "not" (negation), and “if and only if” (biconditional).
Examples of simple propositions were seen earlier, while some examples of compound propositions are:
- "It is not raining." The operator "not" (negation) modifies the phrase "it is raining."
- "It is sunny and it is hot." Here the connective "and" (conjunction) joins the phrases "it is sunny" and "it is hot."
- "I am going to the movies or I am staying home." The connective "or" (disjunction) joins the phrases "I am going to the movies" and "I am staying home."
- "If you study, then you will pass." The connective "if... then..." (conditional) joins the phrases "you study" and "you will pass."
- "A number is even if and only if it is divisible by 2." The logical connective "if and only if" (biconditional) joins the phrases "a number is even" and "it is divisible by 2."
Some more complex examples involving more than one connective:
- "It is not the case that John is coming to the party and Mary is not coming." Here, the "not" connective negates the conjunction "John is coming to the party and Mary is not coming."
- "If it is cold and cloudy, then I will wear a coat or I will stay home." In this proposition, the "if... then..." (conditional) connective joins "it is cold and cloudy" (where "and" joins "it is cold" and "it is cloudy").
The truth or falsity of a compound proposition depends on the truth values of the simple propositions that compose it and the way they are combined. Depending on whether these simple propositions are true or false, the compound proposition will have a corresponding truth value. For example, the proposition “Mars and Venus are planets” is true if the propositions “Mars is a planet” and “Venus is a planet” are both true, which in this case, they are. This analysis is performed using truth tables.
Notation
In logic, propositions are denoted by the last lowercase letters of the alphabet (p, q, r, s, …), and these letters are called propositional variables. The value true is indicated by the letter “V,” the number 1, or the letter “T” (for true); while the value false is indicated by the letter “F” or the number 0.
Each logical connective has a specific symbol, which can be seen in the following table.
| Connective | Symbol |
|---|---|
| Negation | ¬ |
| Conjunction | ∧ |
| Disjunction | ∨ |
| Conditional | → |
| Biconditional | ↔ |
For example, given the following propositions:
- p: "It is raining."
- q: "I will carry an umbrella."
The following new propositions, among others, can be formed:
- ¬p: “It is not raining.”
- ¬q: “I will not carry an umbrella.”
- p ∧ q: "It is raining and I will carry an umbrella."
- p ∨ q: "It is raining or I will carry an umbrella."
- p → q: "If it is raining, then I will carry an umbrella."
- p ↔ q: "It is raining if and only if I will carry an umbrella."
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

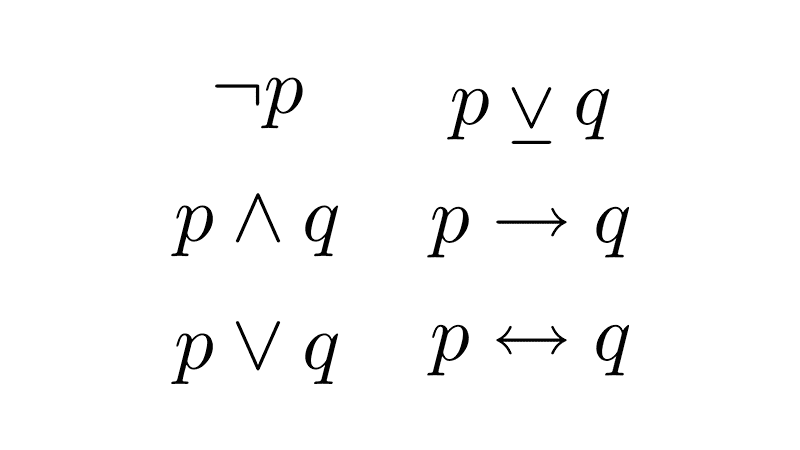
Related posts