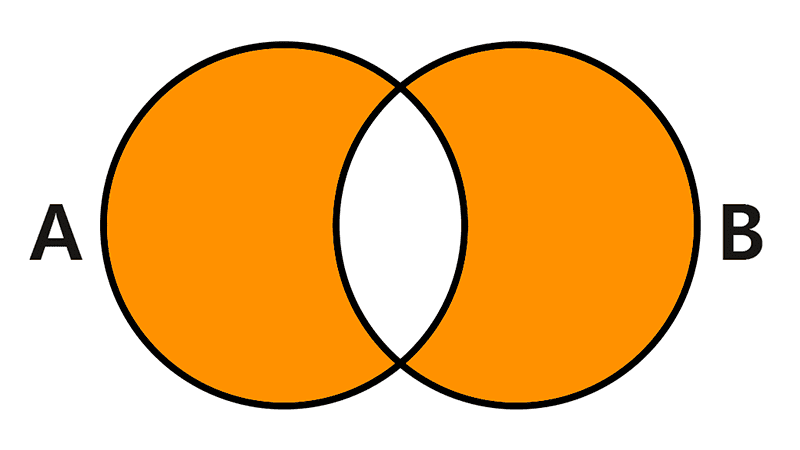
Set Complementation
The complement of a set is a fundamental operation that produces a new set containing all the elements that do not belong to the original set but are present within a reference universal set. The complement of a set A is commonly represented with a prime symbol (A′), an overline (Ā), or a superscript ‘C’ (AC).
Formally, if we have a universal set U and a subset A ⊆ U, the complement of A is defined as the set of all elements of U that are not in A. It is denoted as A′ and expressed in set-builder notation as follows:
A′ = { x | x ∈ U ∧ x ∉ A }
This definition uses a conjunction and a logical negation: an element will be part of the complement if it is in the universal set and at the same time is not in A. This means that the complement of A is, in essence, what A is missing to be equal to the universal set U.
Another useful way to understand this operation is as a set difference: the complement of A is simply the difference between the universal set U and the set A itself. That is:
A′ = U - A
We can find this relationship by analyzing the definition given earlier.
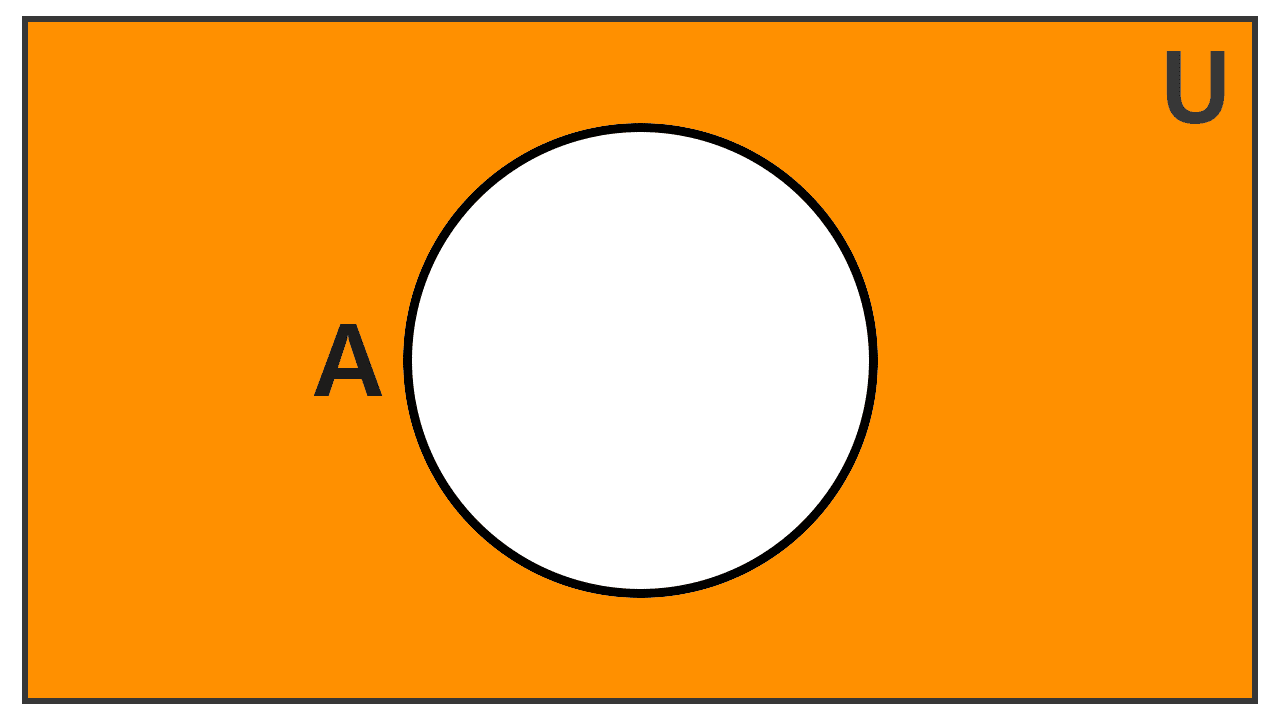
It is also common to define the complement of a set A relative to another set B, which is known as set difference and is denoted as B - A or CBA. This set consists of the elements that belong to B but not to A, meaning B acts as the universal set.
Table of Contents
Examples
It is essential to know that this operation requires a universal set U to be explicitly defined as a reference. In numerical contexts, unless otherwise specified, it is common to consider the set of real numbers (R) as the universal set.
Example 1
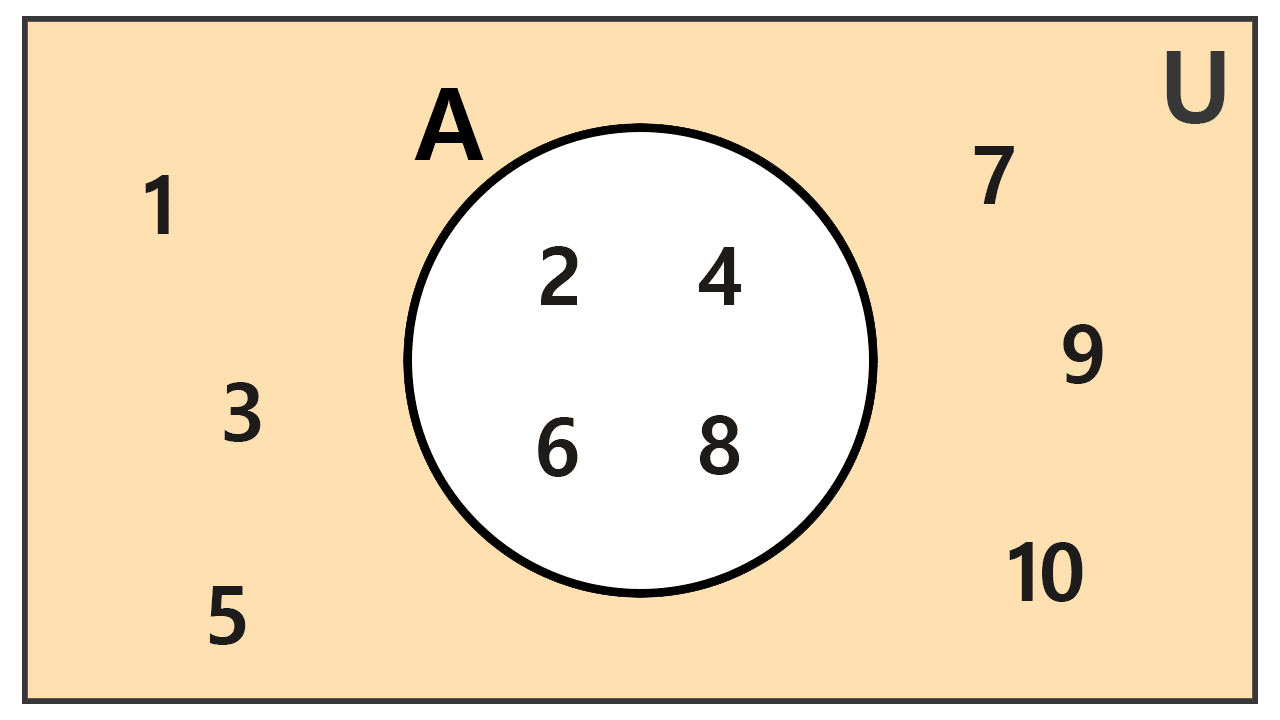
Given the universal set U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and the set A = {2, 4, 6, 8}. Find the complement of A.
Solution
The complement of A, denoted A′, consists of all elements of U that are not in A. We proceed by listing the numbers from 1 to 10 and excluding those that are in A. Thus, the elements 2, 4, 6, and 8 belong to A, so they will not be part of the complement. The new set will be composed of the remaining elements of U:
A′ = {1, 3, 5, 7, 9, 10}
Example 2
Given the universal set formed by the letters of the English alphabet, U = {a, b, c, d, e, f, g, h, i}, and the set B = {a, b, c, d}, calculate B′.
Solution
The complement of B will be all the letters it is missing to be equal to the universal set, that is:
B′ = {e, f, g, h, i}
Example 3
If we take the natural numbers N = {1, 2, 3, ...} as the universal set and define the set P = {2, 4, 6, 8, 10, …} of positive even numbers, find P′.
Solution
The set P′ will be formed by all natural numbers that are not even, that is, the odd numbers. Therefore:
P′ = {1, 3, 5, 7, ...}
Example 4
Considering the universal set of integers Z, find the complement of the set of non-negative integers, A = {0, 1, 2, 3, ...}.
Solution
The complement of A in Z will be the set of all integers that are neither zero nor positive. This corresponds exactly to the set of negative integers:
A′ = {-1, -2, -3, ...}
Example 5
Within the universe of real numbers (R), determine the complement of the set of rational numbers (Q).
Solution
The set of rational numbers Q includes all fractions and finite or repeating decimals. Its complement in R is the set of numbers that cannot be expressed as a fraction, that is, the irrational numbers, such as π or √2. Therefore:
Q′ = I (the set of irrational numbers).
Example 6
Let the universal set be U = {x ∈ Z | -5 ≤ x ≤ 5} and the set F = {-2, -1, 0, 1, 2}. Calculate F′.
Solution
First, we express U by roster method:
U = {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5}
The complement of F is obtained by removing the elements of F from U. Thus, the elements to be removed are -2, -1, 0, 1, and 2. The resulting set is:
F′ = {-5, -4, -3, 3, 4, 5}
Properties
The complementation operation in set theory has a series of fundamental properties that simplify its calculation and relate it to other operations.
1) Complement of the empty set: The complement of the empty set is always the universal set. Since there are no elements in ∅, all elements of U belong to its complement.
∅′ = U
2) Complement of the universal set: Reciprocally, the complement of the universal set is the empty set, as there are no elements outside of U.
U′ = ∅
3) Involution: The complement of the complement of a set is equal to the original set.
(A′)′ = A
4) Union with the complement: The union of any set with its complement always results in the universal set. Together, they contain all possible elements of U.
A ∪ A′ = U
5) Intersection with the complement: A set and its complement are always disjoint (they share no elements). Their intersection is, therefore, the empty set.
A ∩ A′ = ∅
6) De Morgan's Laws: These laws connect complementation with union and intersection, showing how the complement acts on these operations.
The complement of a union is equal to the intersection of the complements:
(A ∪ B)′ = A′ ∩ B′
The complement of an intersection is equal to the union of the complements:
(A ∩ B)′ = A′ ∪ B′
7) Subsets: If a set A is a subset of B, then the complement of B is a subset of the complement of A:
If A ⊆ B, then B′ ⊆ A′.
Leave a Reply



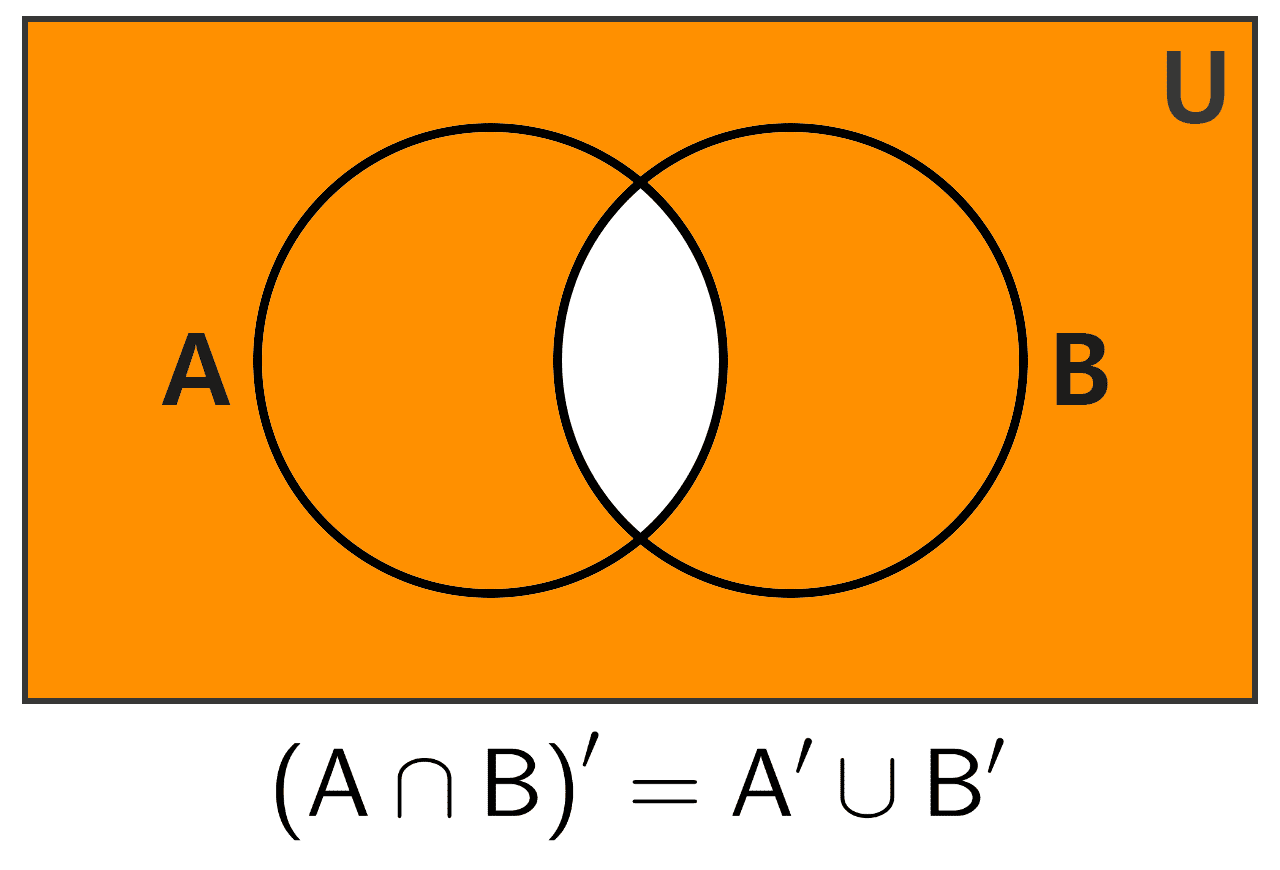

Related posts