
Symmetric Difference of Sets
The symmetric difference of sets is an operation that produces a new set formed by the elements that are in one of the original sets, but not in both. It is represented by the symbol Δ, which corresponds to the Greek capital letter delta and is shaped like a triangle.
Formally, the symmetric difference between two sets A and B is denoted as A Δ B and is expressed in set-builder notation as follows:
A Δ B = { x | x ∈ A ⊻ x ∈ B }
The logical connective of exclusive disjunction means that an element will belong to the symmetric difference if it is in A or in B, but not in both at the same time.
Alternatively, the symmetric difference can be understood as the union of the sets minus their intersection:
A Δ B = (A ∪ B) - (A ∩ B)
Another equivalent way to define it is by combining the simple differences between the sets:
A Δ B = (A - B) ∪ (B - A)
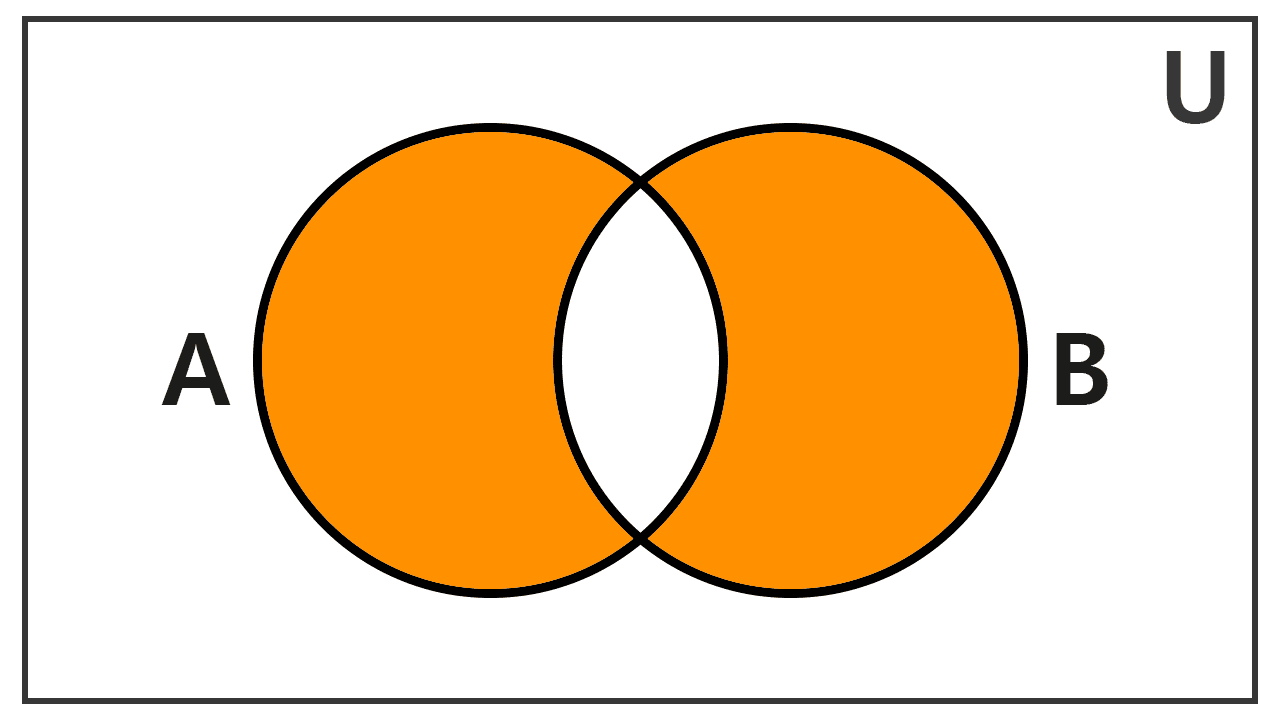
Table of Contents
Examples
To calculate the symmetric difference, we can use two equivalent methods, which always lead to the same result:
Method 1: calculate the union of the sets and subtract their intersection, using this formula:
A Δ B = (A ∪ B) - (A ∩ B)
Method 2: unite the two simple differences between the sets, using this other formula:
A Δ B = (A - B) ∪ (B - A)
Next, we will look at several cases applying these procedures.
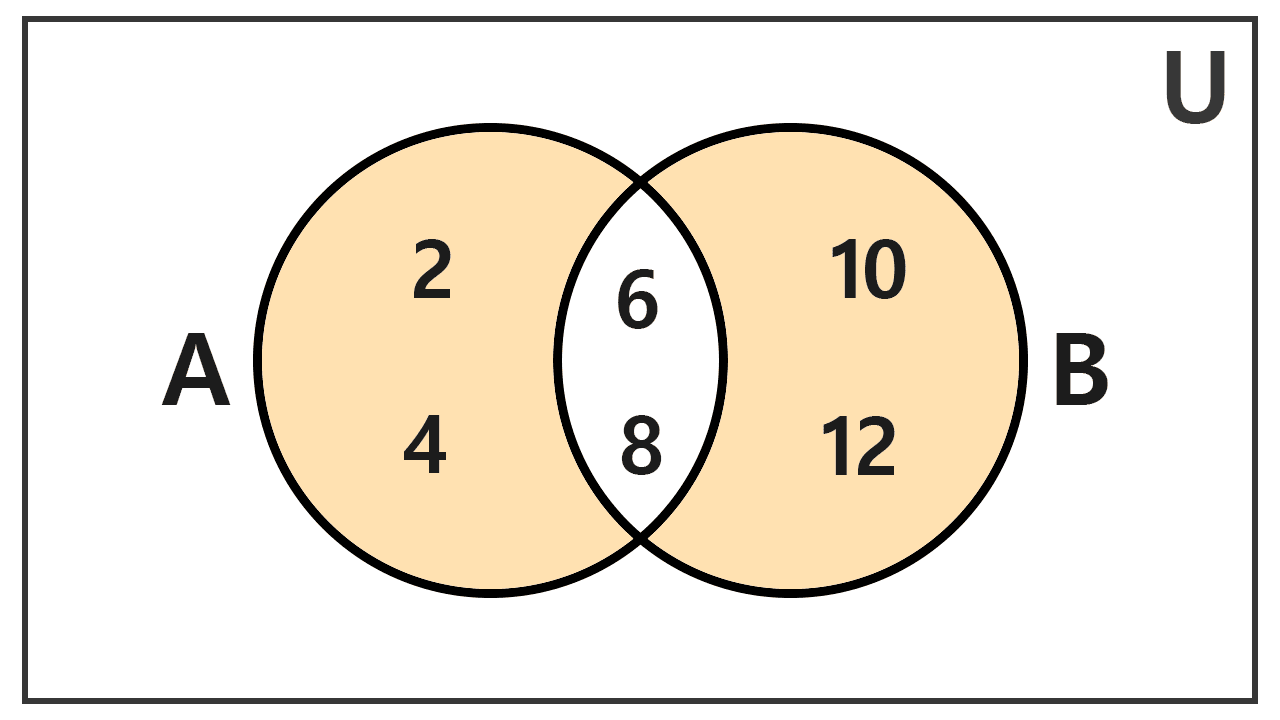
Example 1
Let the sets be A = {2, 4, 6, 8} and B = {6, 8, 10, 12}. Find their symmetric difference.
Solution
We will apply both methods to verify that the result is the same.
Method 1: (A ∪ B) - (A ∩ B)
First, we find the union of A and B: A ∪ B = {2, 4, 6, 8, 10, 12}.
Then, we identify their intersection: A ∩ B = {6, 8}.
Finally, we subtract the intersection from the union:
(A ∪ B) - (A ∩ B) = {2, 4, 6, 8, 10, 12} - {6, 8} = {2, 4, 10, 12}
Method 2: (A - B) ∪ (B - A)
We calculate the elements that are only in A: A - B = {2, 4}.
We calculate the elements that are only in B: B - A = {10, 12}.
We unite both results:
(A - B) ∪ (B - A) = {2, 4} ∪ {10, 12} = {2, 4, 10, 12}
Both methods confirm that the symmetric difference is:
A Δ B = {2, 4, 10, 12}
Example 2
Determine the symmetric difference of C = {a, e, i, o, u} and D = {e, o, b, c, d}.
Solution
We will use the method of uniting the simple differences. To do this, we first find the exclusive elements of C:
C - D = {a, i, u}
Now we identify the exclusive elements of D:
D - C = {b, c, d}
The union of these two sets gives the result:
C Δ D = {a, i, u, b, c, d}
Example 3
Calculate the symmetric difference of E = {1, 3, 5} and F = {2, 4, 6}.
Solution
We apply the method of the union minus the intersection.
The union is E ∪ F = {1, 2, 3, 4, 5, 6}.
Since they have no elements in common, their intersection is empty: E ∩ F = ∅.
Subtracting the empty set does not alter the set, therefore:
E Δ F = {1, 2, 3, 4, 5, 6} - ∅ = {1, 2, 3, 4, 5, 6}
Example 4
Let the sets be P = {10, 20, 30, 40} and Q = {5, 10, 15, 20}. Find P Δ Q.
Solution
We calculate the union and the intersection.
P ∪ Q = {5, 10, 15, 20, 30, 40}
P ∩ Q = {10, 20}
The symmetric difference is the union without the intersection:
P Δ Q = {5, 10, 15, 20, 30, 40} - {10, 20} = {5, 15, 30, 40}
Example 5
Determine the symmetric difference of A = {x ∈ N | x is even ∧ x < 10} and B = {x ∈ N | x is a multiple of 3 ∧ x < 10}.
Solution
First, we express both sets by roster method:
A = {2, 4, 6, 8}
B = {3, 6, 9}
Now, we use the method of uniting the simple differences.
A - B = {2, 4, 8}
B - A = {3, 9}
Uniting both results, we get:
A Δ B = {2, 3, 4, 8, 9}
Example 6
Find the symmetric difference of P = {x ∈ Z | -2 ≤ x ≤ 2} and Q = {x ∈ N | x² < 10}.
Solution
We start by listing the elements of each set.
P includes the integers from -2 to 2: P = {-2, -1, 0, 1, 2}.
Q contains the natural numbers whose square is less than 10: Q = {1, 2, 3}.
We apply the method of the union minus the intersection.
P ∪ Q = {-2, -1, 0, 1, 2, 3}
P ∩ Q = {1, 2}
Therefore, the symmetric difference is:
P Δ Q = (P ∪ Q) - (P ∩ Q) = {-2, -1, 0, 1, 2, 3} - {1, 2} = {-2, -1, 0, 3}
Properties
The symmetric difference operation in set theory has notable characteristics that facilitate its manipulation and calculation.
1) Commutativity: the order of the sets does not alter the result.
A Δ B = B Δ A
2) Associativity: the way the sets are grouped does not affect the final set.
(A Δ B) Δ C = A Δ (B Δ C)
3) Identity element: the symmetric difference of any set with the empty set is the original set.
A Δ ∅ = A
4) Inverse element: every set is its own inverse for this operation; the symmetric difference of a set with itself results in the empty set.
A Δ A = ∅
5) Distributivity over intersection: intersection is distributive over the symmetric difference.
A ∩ (B Δ C) = (A ∩ B) Δ (A ∩ C)
6) Relation with disjoint sets: if two sets are disjoint (they have no elements in common), their symmetric difference is equal to their union.
If A ∩ B = ∅, then A Δ B = A ∪ B
7) Relation with subsets: if one set is a subset of another, the symmetric difference reduces to the simple set difference.
If A ⊆ B, then A Δ B = B - A
If B ⊆ A, then A Δ B = A - B
8) Cancellation law: if the symmetric difference of two sets with a third set is equal, then the two original sets are equal.
If A Δ C = B Δ C, then A = B
Leave a Reply



Related posts