Set Difference

The set difference is a fundamental operation that produces a new set formed by the elements that belong to a first set but not to a second. It is represented by the minus sign "-".

Set difference is not commutative. This means that, in general, the order of the sets matters: A - B is not the same as B - A. While the first operation takes the elements of A that are not in B, the second takes the elements of B that are not in A.

Another way to name the difference between A and B is the relative complement of B with respect to A, symbolized as C_AB. Also, a different way to symbolize the difference A - B is by using a backslash instead of the minus sign, like this: A \ B.

Examples

Below are some examples of this operation.

Example 1

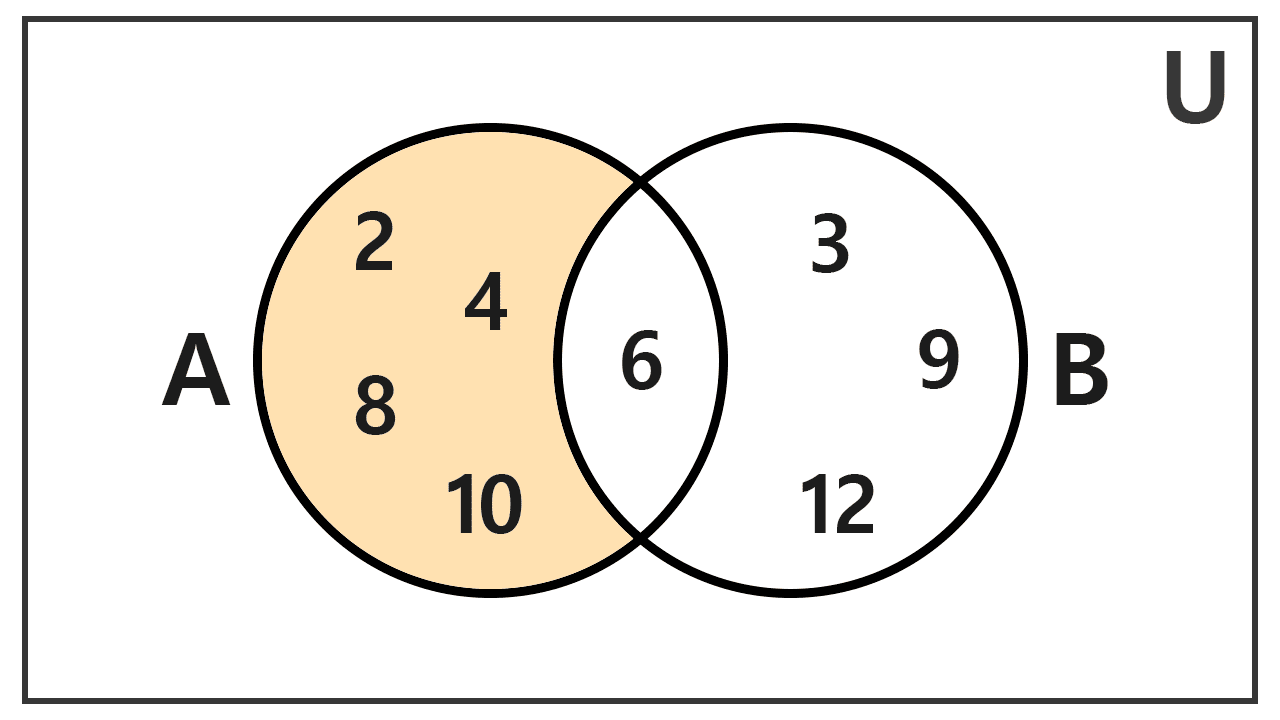
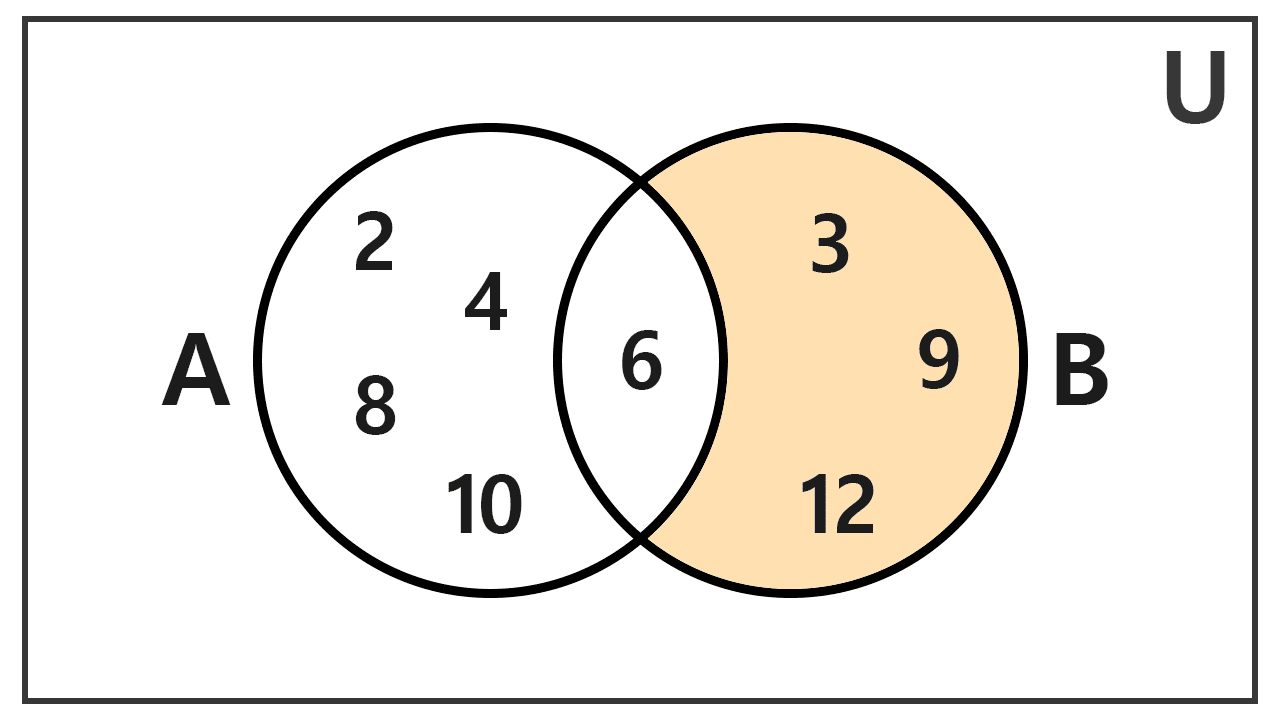
Given the sets A = {2, 4, 6, 8, 10} and B = {3, 6, 9, 12}. Calculate A - B and B - A.

Solution

To get A - B, we take the elements of A and exclude those that also belong to B. In A, the elements are 2, 4, 6, 8, and 10. Of these, 6 is also present in B, so we remove it. Thus:

A - B = {2, 4, 8, 10}

To find B - A, we consider the elements of B and remove those that are in A. B contains 3, 6, 9, and 12. The number 6 appears in A, so we remove it. The result is 

B - A = {3, 9, 12}

In this case, both differences are non-empty sets and are different from each other.

Example 2

Given C = {a, e, i, o, u} and D = {a, b, c, d, e}, determine C - D and D - C.

Solution

We first calculate C - D. We identify the elements of C that are not in D: the vowels i, o, and u do not appear in D, so:

C - D = {i, o, u}

Now, for D - C, we take the elements of D and remove those that belong to C. The letters b, c, and d from D are not in C, so:

D - C = {b, c, d}

Example 3

Consider E = {1, 3, 5, 7, 9} and F = {2, 4, 6, 8}. Find E - F and F - E.

Solution

E - F consists of the elements of E that are not in F. Since E and F share no elements, all elements of E are kept: 

E - F = {1, 3, 5, 7, 9} = E

For F - E, all elements of F are kept, since none belong to E. Therefore, 

F - E = {2, 4, 6, 8} = F

Here, although the sets are disjoint, E - F ≠ F - E, which reinforces the non-commutativity of the operation.

Example 4

Let G = {x, y, z} and H = {x, y, z}. Find G - H and H - G.

Solution

G - H requires the elements of G that are not in H. Since G and H are equal, there are no elements in G that are not in H. Therefore, G - H = ∅. Similarly, H - G looks for the elements of H that are not in G. Since the sets are equal, the result is also the empty set: H - G = ∅.

Example 5

Let N be the set of natural numbers and P be the set of positive even numbers. Calculate N - P.

Solution

We write some elements of both sets:

N = {1, 2, 3, 4, 5, 6, …}

P = {2, 4, 6, 8, 10, 12, …}

If we remove all elements of P from N, we are left with the set of odd numbers I:

I = {1, 3, 5, 7, 9, 11, …}

If we were to calculate the difference P minus the set N, we would get the empty set, since all positive even numbers are also natural numbers.

Properties

The difference operation in set theory has a set of properties and relationships with other operations.

1) Non-commutativity: the order of the sets in a difference does alter the result.

A - B ≠ B - A

2) Non-associativity: the way sets are grouped affects the final result.

(A - B) - C ≠ A - (B - C)

3) Identity element: the difference of any set with the empty set is the original set. The empty set acts as the right identity element.

A - ∅ = A

4) Difference with the universal set: the difference of a set with the universal set is the empty set.

A - U = ∅

5) Relationship with the complement: set difference is used to define the complement of a set: the complement of A is the difference between the universal set and A.

A' = U - A

6) Difference as intersection: the difference between two sets is equal to the intersection of the first with the complement of the second.

A - B = A ∩ B'

This is proven by definition:

A - B = {x | x ∈ A ∧ x ∉ B} = { x | x ∈ A ∧ x ∈ B’ } = A ∩ B'

7) Difference of a set with itself: the difference of any set with itself is always the empty set.

A - A = ∅

8) Disjoint sets: if two sets are disjoint (they share no elements), then their difference is equal to the first set. 

If A and B are disjoint (A ∩ B = ∅), then:

A - B = A

B - A = B

9) Inclusion property: if a set is a subset of another, their difference is the empty set.

If A ⊆ B, then A - B = ∅

10) Distributivity of intersection over difference: the intersection is distributive with respect to the difference.

A ∩ (B - C) = (A ∩ B) - (A ∩ C)

To prove this property, we start with the expression on the left-hand side and apply the definition of difference as an intersection with the complement:

A ∩ (B - C) = A ∩ (B ∩ C') = (A ∩ B) ∩ C' (1)

Now we consider the right-hand side of the equality. We again apply the definition of difference:

(A ∩ B) - (A ∩ C) = (A ∩ B) ∩ (A ∩ C)'

We use De Morgan's Law to transform the complement of an intersection:

= (A ∩ B) ∩ (A' ∪ C')

Now we apply the distributive property of intersection over union:

= [(A ∩ B) ∩ A'] ∪ [(A ∩ B) ∩ C']

Let's analyze the first term: (A ∩ B) ∩ A' = A ∩ B ∩ A'. Since A ∩ A' = ∅, we have: A ∩ B ∩ A' = ∅. Therefore, the expression simplifies to:

= ∅ ∪ [(A ∩ B) ∩ C'] = (A ∩ B) ∩ C' (2)

Comparing results (1) and (2), we get:

A ∩ (B - C) = (A ∩ B) ∩ C' = (A ∩ B) - (A ∩ C)

Thus, the equality is proven.