
Intersection of Sets
The intersection of sets is a fundamental operation that produces a new set formed only by the elements that the original sets share, that is, the common elements. It is represented by the symbol “∩”.
Formally, the intersection of two sets A and B is defined as the set of all elements that belong to both A and B. It is denoted as A ∩ B and is expressed in set-builder notation as follows:
A ∩ B = { x | x ∈ A ∧ x ∈ B }
This definition uses a conjunction (the logical connective "and"), which means an element will only be part of the intersection if it is present in both sets simultaneously.
The main difference between the union and intersection lies in the elements they include: while the union combines all elements from the involved sets, the intersection is limited exclusively to those that are common to all of them.
Table of Contents
Examples
Below, we will look at several cases of set intersection. It is key to know that if there are no common elements, the result will be the empty set (Ø), and sets whose intersection is empty are called disjoint.
Example 1
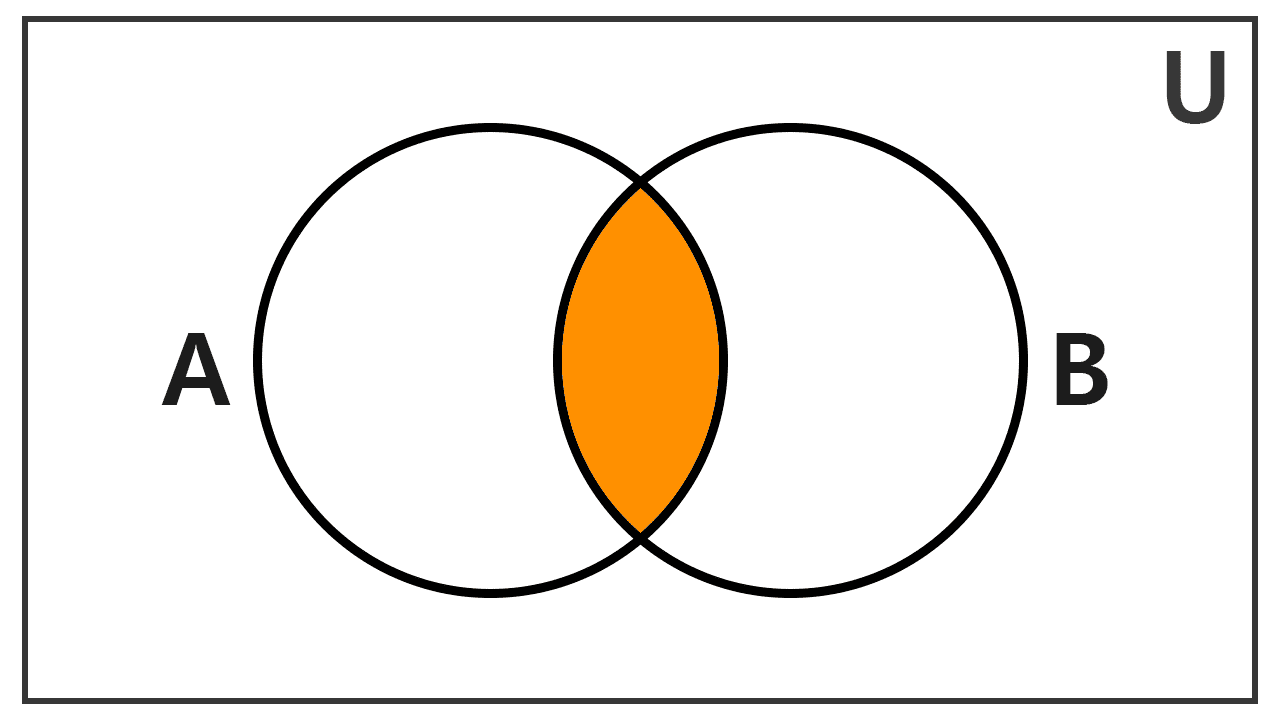
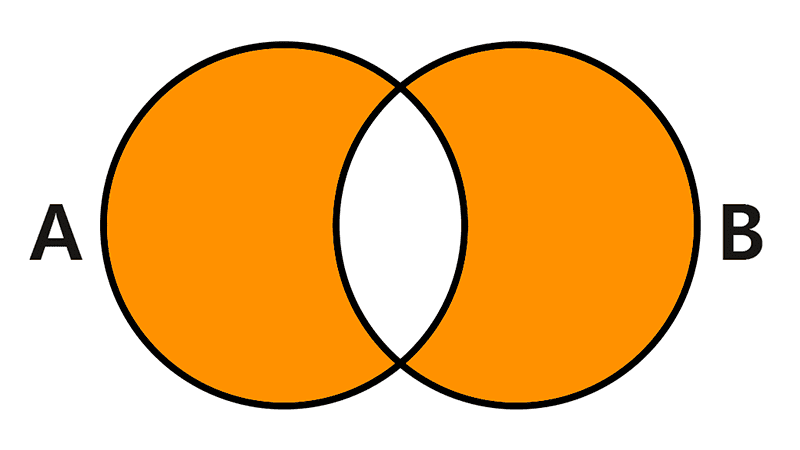
Let sets be A = {1, 2, 3} and B = {3, 4, 5}. Find their intersection.
Solution
We identify the elements that are present in both sets. We observe that only the number 3 meets this condition. Therefore, the intersection is:
A ∩ B = {3}
Graphically, the solution is:
Example 2
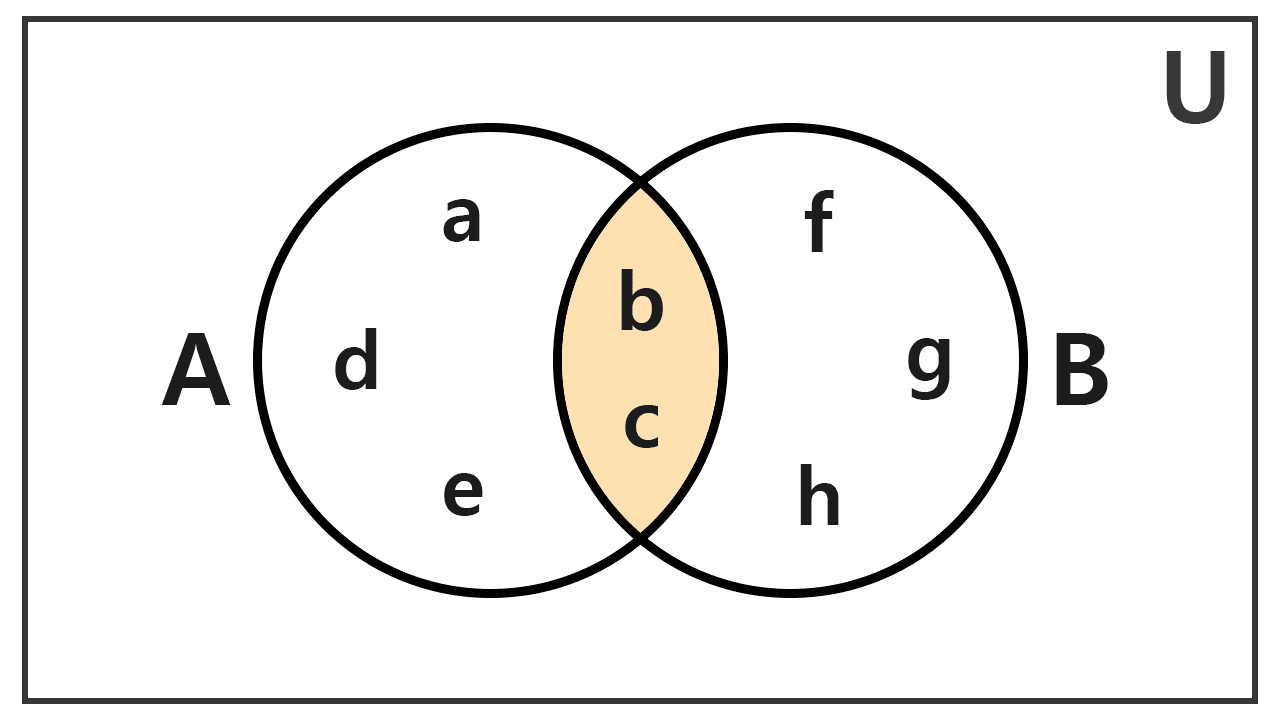
Determine the intersection of A = {a, b, c, d, e} and B = {b, c, f, g, h}.
Solution
We look for the elements that belong to A and B simultaneously. The letters 'b' and 'c' are the only ones that appear in both. Thus, the intersection set is:
A ∩ B = {b, c}
Example 3
Calculate the intersection of E = {-1, -2, -3} and F = {1, 2, 3}.
Solution
In this case, sets E and F have no elements in common; they are disjoint sets. The intersection of two disjoint sets is always the empty set:
E ∩ F = ∅
Example 4
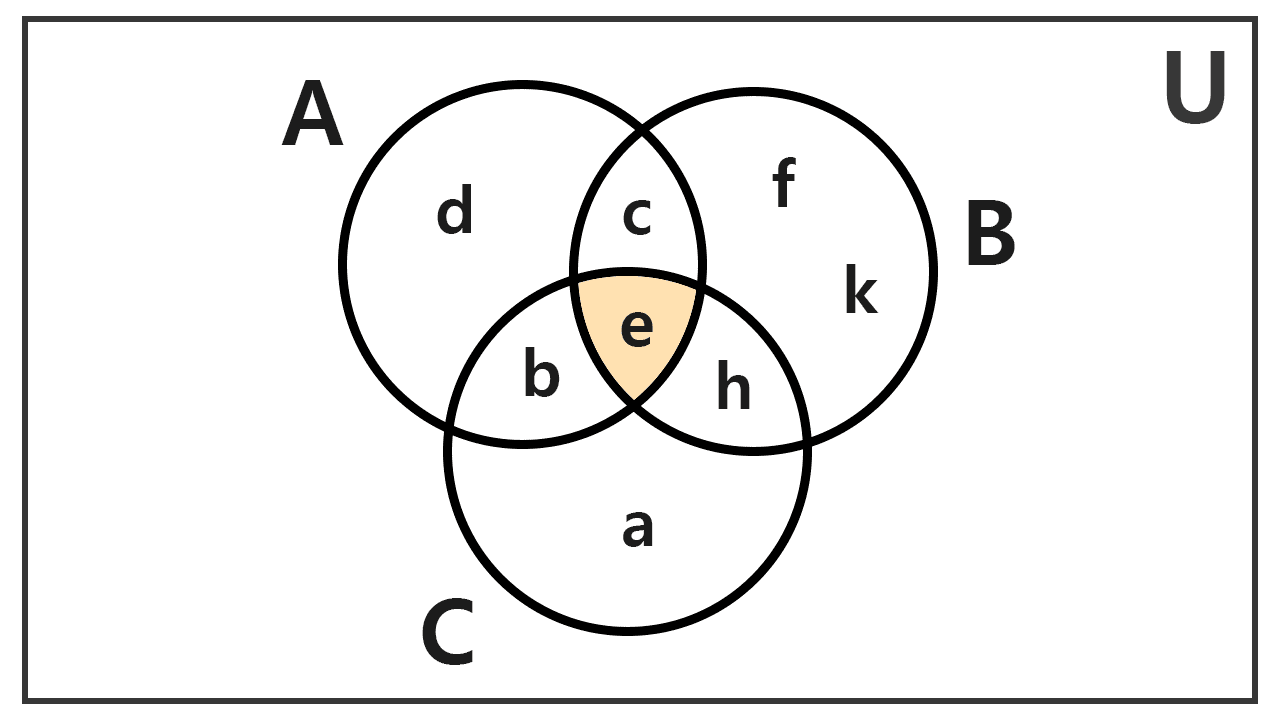
Given the sets A = {b, c, d, e}, B = {c, e, h, f, k} and C = {a, b, e, h}, calculate the intersection of the three.
Solution
We can proceed step by step. First, we calculate the intersection of A and B: the common elements are 'c' and 'e', so:
A ∩ B = {c, e}
Next, we intersect this result with set C.
(A ∩ B) ∩ C = {c, e} ∩ {a, b, e, h}
Of the elements {c, e}, only 'e' is present in C. Therefore, the final intersection of the three sets is the following singleton set:
A ∩ B ∩ C = {e}
Graphically, the solution is:
Note: due to the associative and commutative properties of intersection, the order in which we calculate the intersections does not affect the result. Thus, we could have first calculated A ∩ C or B ∩ C and then found the intersection with the remaining set.
Example 5
Determine the intersection of A = {1, 2, 4, 7}, B = {2, 3, 4, 5, 9}, and C = {4, 5, 6, 7}.
Solution
We start by finding the elements that A and B have in common, which are 2 and 4:
A ∩ B = {2, 4}
Then, we look for the elements of this new set that also belong to C. Of {2, 4}, only the number 4 is found in C. Thus, the intersection of the three sets is:
A ∩ B ∩ C = {4}
Example 6
Let the sets be M = {x ∈ N | x is a multiple of 3 and x < 15} and N = {x ∈ N | x is even and x ≤ 12}. Find M ∩ N.
Solution
The sets are given in set-builder notation, so we first express them in roster form to identify their elements.
Set M is formed by the natural numbers that are multiples of 3 and less than 15:
M = {3, 6, 9, 12}
Set N contains the even natural numbers less than or equal to 12:
N = {2, 4, 6, 8, 10, 12}
The intersection will be formed by the common elements of both sets. The numbers that appear in M and N are 6 and 12. Therefore, the intersection is:
M ∩ N = {6, 12}
Properties
The intersection operation in set theory has essential characteristics that facilitate its handling and calculation.
1) Commutativity: the order of the sets does not change the result.
A ∩ B = B ∩ A
2) Associativity: the grouping of sets when intersecting does not affect the final set.
(A ∩ B) ∩ C = A ∩ (B ∩ C)
3) Idempotence: the intersection of a set with itself returns the same set.
A ∩ A = A
4) Identity element: intersecting any set with the universal set yields the original set.
A ∩ U = A
5) Absorption property: the intersection of any set with the empty set results in the empty set.
A ∩ ∅ = ∅
6) Distributivity over union: intersection distributes over the union of sets.
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
7) De Morgan's Law: the complement of an intersection is equivalent to the union of the complements.
(A ∩ B)’ = A’ ∪ B’
8) Cardinality: for finite sets, the size of the intersection is related to the individual sizes and their union.
|A ∩ B| = |A| + |B| - |A ∪ B|
9) Relations with subsets:
- If one set is contained in another, their intersection is the smaller set: if A ⊆ B, then A ∩ B = A.
- The intersection of two sets is always a subset of each of them: A ∩ B ⊆ A and A ∩ B ⊆ B.
- If two sets are subsets of a third set, their intersection is also a subset of it: if A ⊆ C and B ⊆ C, then A ∩ B ⊆ C
- If a set is a subset of two other sets, it is also a subset of their intersection: if X ⊆ A and X ⊆ B, then X ⊆ A ∩ B.
Leave a Reply


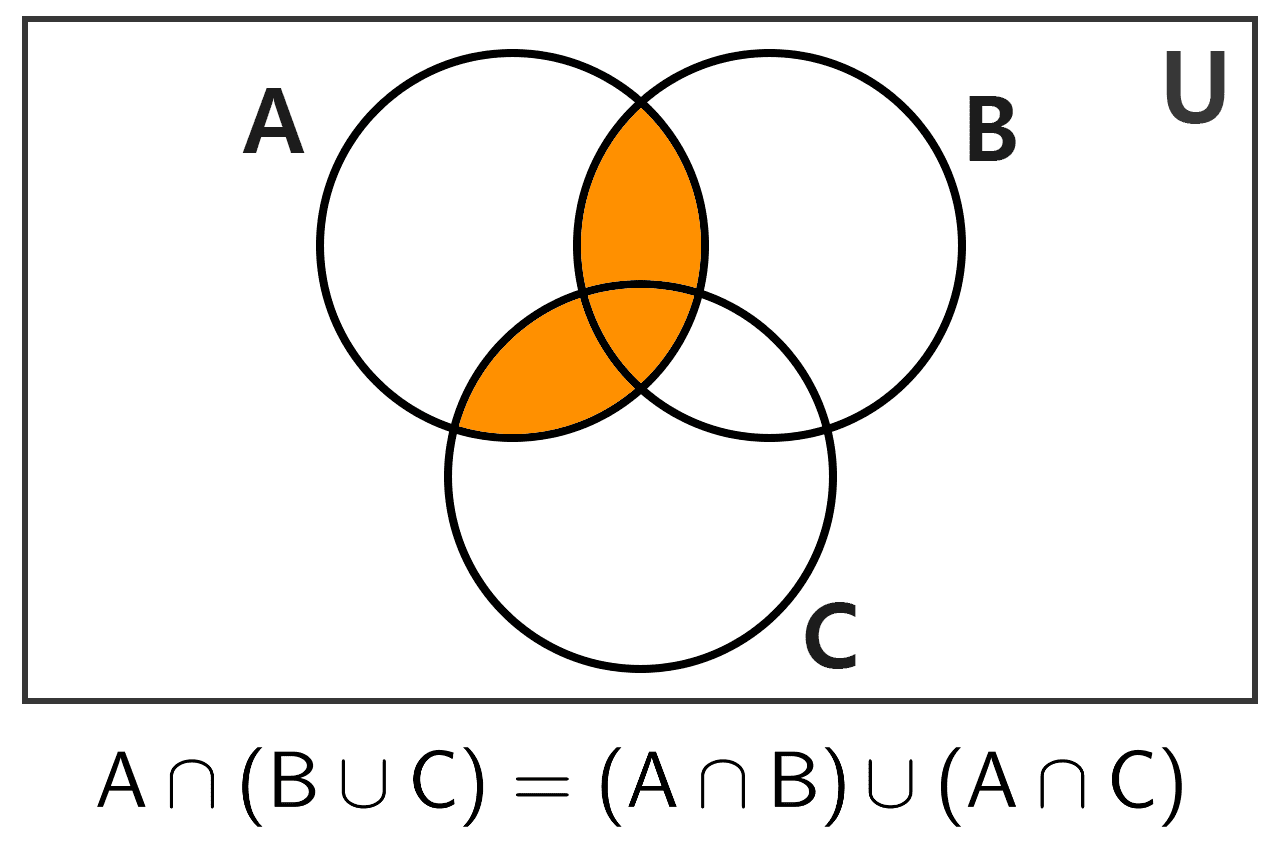
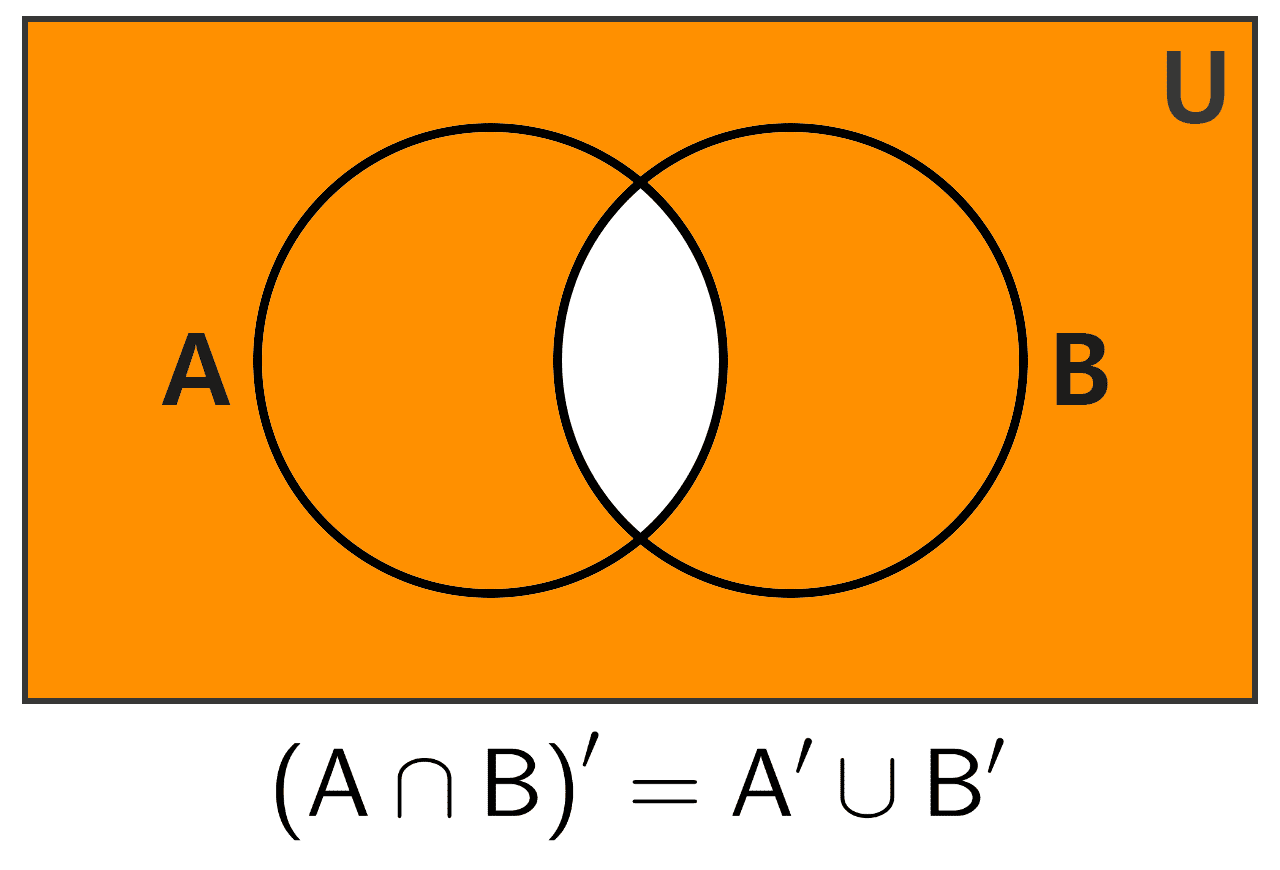

Related posts