Logical Equivalences
In propositional logic, two expressions are logically equivalent when they have identical truth tables for all combinations of truth values of their variables. This means they assert the same thing, just in a different way. In practice, we can substitute one for the other in any expression without altering its validity, and the equivalence relation is symbolized with ≡.
The fundamental tool for proving an equivalence is the biconditional (↔). If the proposition p ↔ q is a tautology (it is always true), then p and q are logically equivalent, which we denote as p ≡ q. To prove that two propositions are equivalent, we can construct their truth tables; if the final result column is identical for both, they are logically equivalent.
Table of Contents
List of logical equivalences
Below, we will see the most important equivalences in mathematical logic.
Fundamental equivalences
In the following properties, V is a tautology (a proposition that is always true), while F is a contradiction (a proposition that is always false).
| Name | Formula | Description |
|---|---|---|
| Identity Laws | p ≡ p p → p p ∧ V ≡ p p ∨ F ≡ p | Every proposition is identical to itself. If a proposition is true, then it is true, and if it is false, then it is false. |
| Law of Non-Contradiction | ¬ (p ∧ ¬p) | A proposition cannot be true and false at the same time. |
| Law of the Excluded Middle | p ∨ ¬p | A proposition is either true or false; there is no third option. |
| Double Negation | ¬(¬p) ≡ p | Stating that something is not false is the same as stating that it is true. |
| Idempotent Laws | p ∨ p ≡ p p ∧ p ≡ p | Repeating the same proposition with "and" or "or" adds no new information. |
| Domination Laws | p ∨ V ≡ V p ∧ F ≡ F | The disjunction of a proposition and a tautology is always true. The conjunction of a proposition and a contradiction is always false. |
| Commutative Laws | p ∨ q ≡ q ∨ p p ∧ q ≡ q ∧ p | The order of propositions in a conjunction or disjunction does not alter the result. |
| Associative Laws | (p ∨ q) ∨ r ≡ p ∨ (q ∨ r) (p ∧ q) ∧ r ≡ p ∧ (q ∧ r) | When we have the same connective (conjunction or disjunction), the grouping does not matter. |
| Distributive Laws | p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r) p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) | Conjunction and disjunction can be distributed over each other, similar to algebra. |
| Absorption Laws | p ∨ (p ∧ q) ≡ p p ∧ (p ∨ q) ≡ p | The disjunction of a proposition with a conjunction in which it also appears is equivalent to the original proposition; the same applies if the symbols are interchanged. |
We will demonstrate that the proposition ¬(¬p) is equivalent to p. To do this, we construct the truth table:
| p | ¬p | ¬(¬p) |
|---|---|---|
| V | F | V |
| F | V | F |
The values in the first column p match those in the ¬(¬p) column in every row. Therefore, we can affirm that they are equivalent propositions, and we write ¬(¬p) ≡ p.
We can do the same when there are more variables. Let's demonstrate the commutativity of disjunction: p ∨ q ≡ q ∨ p:
| p | q | p ∨ q | q ∨ p |
|---|---|---|---|
| V | V | V | V |
| V | F | V | V |
| F | V | V | V |
| F | F | F | F |
We can see that the columns for p ∨ q and q ∨ p are exactly the same, so we can safely state that they are equivalent expressions.
De Morgan's Laws
| Name | Formula | Description |
|---|---|---|
| Negation of Conjunction | ¬(p ∧ q) ≡ ¬p ∨ ¬q | The negation of a conjunction is equivalent to the disjunction of the negations. |
| Negation of Disjunction | ¬(p ∨ q) ≡ ¬p ∧ ¬q | The negation of a disjunction is equivalent to the conjunction of the negations. |
Laws of the Conditional and Biconditional
| Name | Formula | Description |
|---|---|---|
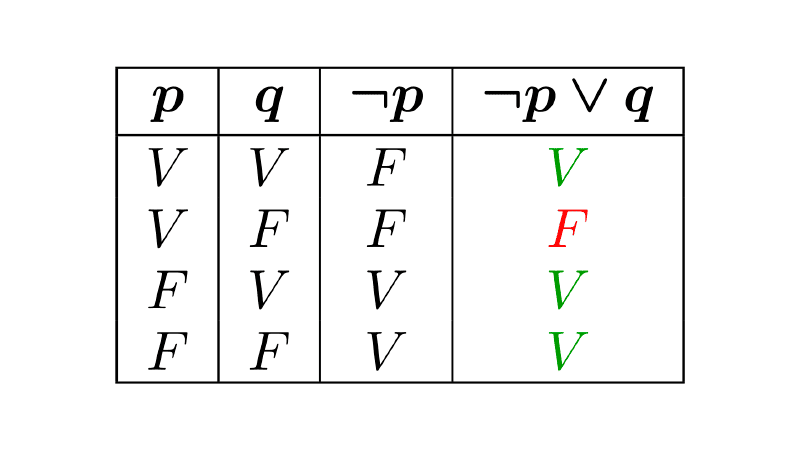
| Definition of the Conditional | p → q ≡ ¬p ∨ q | A conditional is equivalent to the disjunction of the negation of the antecedent and the consequent. |
| Negation of the Conditional | ¬(p → q) ≡ p ∧ ¬q | The negation of a conditional is equivalent to the conjunction of the antecedent and the negation of the consequent. |
| Law of Contraposition | p → q ≡ ¬q → ¬p | An implication is equivalent to its contrapositive. |
| Expansion Laws | (p → q) ≡ (p ∨ q) ↔ q (p → q) ≡ (p ∧ q) ↔ p | A conditional can be expressed as a biconditional between the conjunction (or disjunction) of its components and the consequent (or the antecedent). |
| Definition of Biconditional | p ↔ q ≡ (p → q) ∧ (q → p) | The biconditional is equivalent to the conjunction of two conditionals: one forward and one backward. |
| Negation of the Biconditional | ¬(p ↔ q) ≡ (p ∧ ¬q) ∨ (¬p ∧ q) | Negating a biconditional is the same as stating that one proposition is true and the other is false, or vice versa. |
| Contrapositive of the Biconditional | (p ↔ q) ≡ (¬q ↔ ¬p) | The biconditional of two propositions is equivalent to the biconditional of their negations. |
Application in Simplifying Propositions
The true power of logical equivalences is seen when simplifying complex propositions. An equivalence like p ∧ q ≡ q ∧ p tells us that in any expression where p ∧ q appears, we can directly replace it with q ∧ p without altering the overall meaning. This systematic substitution process allows for reducing long and intricate formulas to simpler, more manageable ones.
Exercise: simplify the following propositional expressions using logical equivalences.
- ¬(p ∨ q) ∨ (¬p ∧ q)
- (p → q) ∧ (p ∨ q)
- ¬p → (q → p)
- (p ∧ ¬q) ∨ (p ∧ q)
- ¬(p → q) ∨ (¬p ∧ ¬q)
Solution 1
Original statement: ¬(p ∨ q) ∨ (¬p ∧ q)
Let's simplify this expression. We will start by applying De Morgan's Law and then distribute to find terms that cancel out.
¬(p ∨ q) ∨ (¬p ∧ q) (original expression)
(¬p ∧ ¬q) ∨ (¬p ∧ q) (De Morgan's law on ¬(p ∨ q))
¬p ∧ (¬q ∨ q) (inverse distributive law, factoring out ¬p)
¬p ∧ V (law of the excluded middle: ¬q ∨ q is a tautology, V)
¬p (identity law)
The proposition simplifies to ¬p.
Solution 2
Original statement: (p → q) ∧ (p ∨ q)
We will begin by transforming the conditional (→) into its equivalent disjunction.
(p → q) ∧ (p ∨ q) (original expression)
(¬p ∨ q) ∧ (p ∨ q) (definition of conditional)
(q ∨ ¬p) ∧ (q ∨ p) (commutative law in both parentheses)
q ∨ (¬p ∧ p) (inverse distributive law, factoring out q)
q ∨ F (because ¬p ∧ p is a contradiction, F)
q (Identity law)
The proposition simplifies to q.
Solution 3
Original statement: ¬p → (q → p)
We will transform all conditionals to work only with conjunctions and disjunctions. Then, we will simplify using the complement laws.
¬p → (q → p) (original expression)
¬(¬p) ∨ (q → p) (definition of implication)
p ∨ (q → p) (double negation)
p ∨ (¬q ∨ p) (definition of implication)
p ∨ (p ∨ ¬q) (commutative law)
(p ∨ p) ∨ ¬q (associative law)
p ∨ ¬q (idempotent law)
Solution 4
Original statement: (p ∧ ¬q) ∨ (p ∧ q)
This is a clear case where we can apply the distributive law 'in reverse' to factor out the common variable and simplify.
(p ∧ ¬q) ∨ (p ∧ q) (original expression)
p ∧ (¬q ∨ q) (distributive law, factoring out p)
p ∧ V (law of the excluded middle: ¬q ∨ q is a tautology, V)
p (identity law)
Solution 5
Original statement: ¬(p → q) ∨ (¬p ∧ ¬q)
We start by negating the conditional. Then, we group terms to arrive at a simplification.
¬(p → q) ∨ (¬p ∧ ¬q) (original expression)
¬(¬p ∨ q) ∨ (¬p ∧ ¬q) (definition of conditional)
(¬¬p ∧ ¬q) ∨ (¬p ∧ ¬q) (De Morgan's law)
(p ∧ ¬q) ∨ (¬p ∧ ¬q) (double negation)
¬q ∧ (p ∨ ¬p) (distributive law, factoring out ¬q)
¬q ∧ V (law of the excluded middle: p ∨ ¬p is a tautology, V)
¬q (Identity law)
Leave a Reply

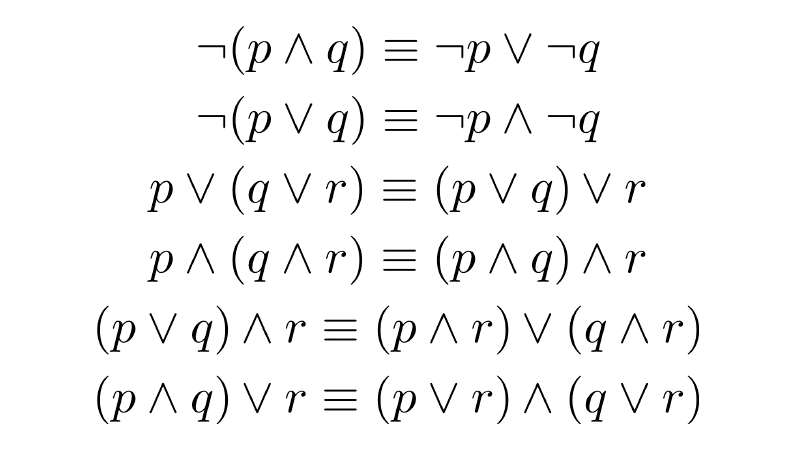
Related posts