Exclusive Disjunction
Exclusive disjunction, also known as XOR (exclusive OR), is a logical connective that joins two propositions and returns a true value only when exactly one of them is true. It is represented by the symbol ⊻ or ⊕ and is read as "either… or…, but not both."
Unlike inclusive disjunction (∨), which allows both propositions to be true, exclusive disjunction excludes that possibility. In other words, it is true only when the two propositions have different truth values.
Some examples of exclusive disjunction are:
- "The light is either on or off": a lamp cannot be on and off at the same time. If one is true, the other is automatically false.
- "That animal is either a dog or a cat": if the animal is a dog, it cannot be a cat, and vice versa. Both possibilities cannot be true at the same time for the same individual.
- "The key is either inside the drawer or outside of it": the key cannot be in both places simultaneously; it must be in only one of the two states.
- If p: "9 is even" and q: "9 is prime", then p ⊻ q is "the number 9 is either even or prime, but not both". This proposition is false because p and q have the same truth value, both being false.
Table of Contents
Truth Table
As we mentioned earlier, strong or exclusive disjunction is true only when one of the two propositions is true, and it is false when both are true or both are false. This behavior is represented in the following truth table:
| p | q | p ⊻ q |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
Examples illustrating the truth table of the strong disjunction:
- "Either 7 is odd or 7 is prime": both propositions are true (7 is odd and it is prime), so the exclusive disjunction is false.
- "4 is even ⊻ 4 is prime": the first proposition is true (4 is even) and the second is false (4 is not prime), so the exclusive disjunction is true.
- "Either 9 is prime or 10 is positive, but not both": the first proposition is false and the second is true (9 is not prime, but 10 is positive), therefore the compound proposition is true.
- "Either 15 is even or 15 is prime, but not both": both propositions are false (15 is neither even nor prime), so the exclusive disjunction is false.
Properties
Exclusive disjunction has a series of properties that we will see next.
1) Commutativity: the order of the propositions does not alter the result.
p ⊻ q ≡ q ⊻ p
2) Associativity: when there are more than two propositions connected by an exclusive disjunction, the grouping does not alter the result.
(p ⊻ q) ⊻ r ≡ p ⊻ (q ⊻ r)
3) Distributivity over conjunction: exclusive disjunction distributes over conjunction.
p ∧ (q ⊻ r) ≡ (p ∧ q) ⊻ (p ∧ r)
4) Neutral element: a contradiction (a proposition that is always false, F) acts as the neutral or identity element.
p ⊻ F ≡ p
5) Inverse element or self-negation: each proposition is its own inverse.
p ⊻ p ≡ F
6) Relationship with negation: negating one of the inputs is equivalent to negating the entire expression.
p ⊻ ¬q ≡ ¬(p ⊻ q)
¬p ⊻ q ≡ ¬(p ⊻ q)
7) Cancellation: if p ⊻ q ≡ p ⊻ r, then p can be "canceled," concluding that q ≡ r.
8) Equivalences with other operators: strong disjunction can be expressed using the basic operators (∧, ∨, ¬) in several ways:
p ⊻ q ≡ (p ∧ ¬q) ∨ (¬p ∧ q)
(This is the definition itself: "p and not q, or not p and q").
p ⊻ q ≡ (p ∨ q) ∧ ¬(p ∧ q)
("One or the other, but not both").
Exclusive disjunction is the negation of the biconditional: while p ↔ q is true when p and q have the same truth value, p ⊻ q is true when they have different values.
p ⊻ q ≡ ¬(p ↔ q)
Exclusive Disjunction in Sets
In set theory, exclusive disjunction has its direct equivalent in the symmetric difference: an operation that combines two sets to form a new one containing elements that belong to one of the sets, but not to both.
The symmetric difference between two sets A and B, denoted as A Δ B, is formally defined as:
A Δ B = { x | x ∈ A ⊻ x ∈ B }
An element x belongs to the symmetric difference if it is in A or in B, but not in both at the same time.
Examples
- Given A = {1, 2, 3} and B = {2, 3, 4}, their symmetric difference is A Δ B = {1, 4}. The elements 2 and 3, which belong to both sets, are excluded from the result.
- If C = {a, e, i} and D = {e, o, u}, then C Δ D = {a, i, o, u}. Only the vowel "e" is excluded for appearing in both sets.
Properties of the symmetric difference:
- Commutativity: A Δ B = B Δ A
- Associativity: (A Δ B) Δ C = A Δ (B Δ C)
- Distributive Intersection: A ∩ (B Δ C) = (A ∩ B) Δ (A ∩ C)
- Neutral element: A Δ ∅ = A (∅ is the empty set).
- Self-inverse: A Δ A = ∅
- Relationship with union and intersection: A Δ B = (A ∪ B) - (A ∩ B)
Exclusive Disjunction in Logic Circuits
In digital electronics, exclusive disjunction is physically implemented by the XOR logic gate. This component receives two input signals and produces an output that follows the same behavior as the ⊻ operator.
The XOR gate returns a value of 1 (true) only when its inputs are different, and 0 (false) when both inputs are the same. This feature makes it essential for operations where detecting differences is crucial.
| Input A | Input B | Output (A XOR B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
In programming, exclusive disjunction has a direct representation in several languages through the “^” operator. This symbol is consistently used in languages like C, C++, Java, and Python to perform the XOR operation between two boolean values or bits. For example, the expression “a ^ b” returns true only when the values of “a” and “b” are different.
Did you find this useful? Rate it!
Leave a Reply

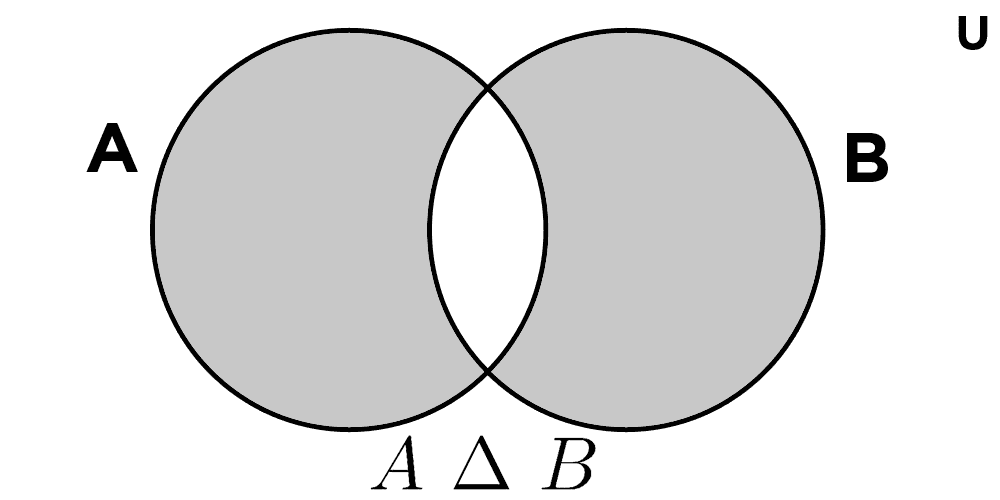
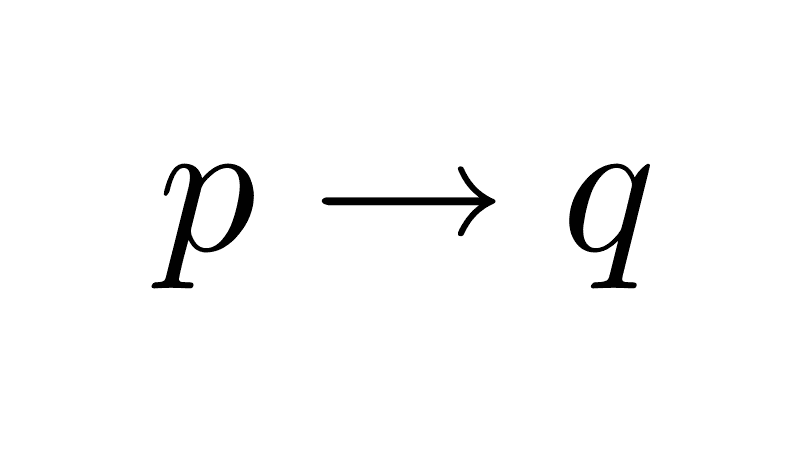
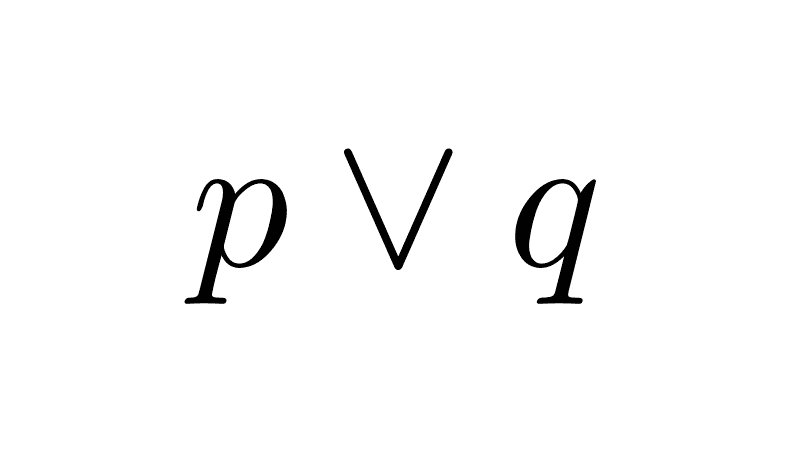
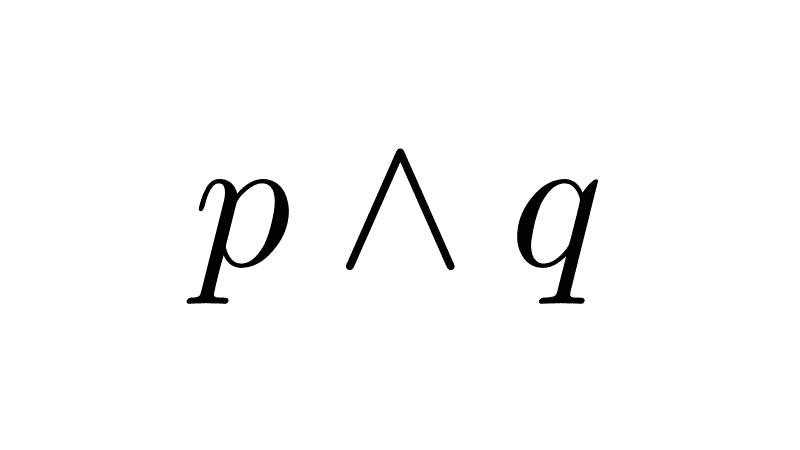
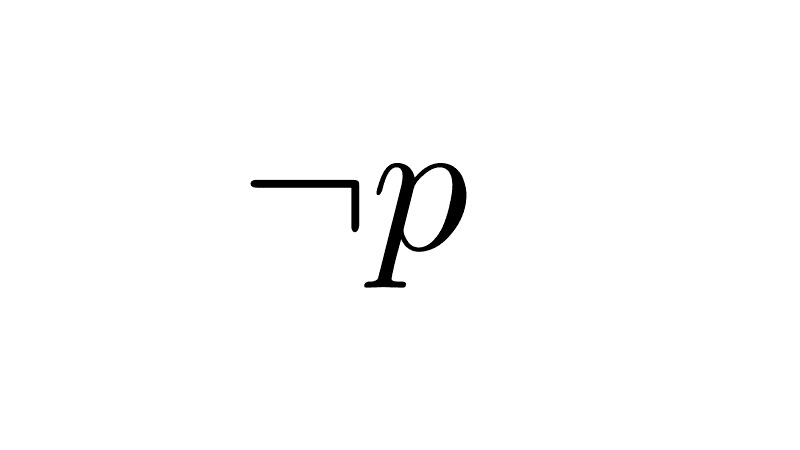
Related posts