Inclusive Disjunction
Disjunction, also known as inclusive or weak disjunction, is a logical connective that combines two simple propositions to form a compound proposition, which is true when at least one of the simple propositions is true, and is false if both are false. Disjunction is represented by the symbol ∨ and is read as “or.”
This connective represents the everyday concept of "or" in its broadest and most inclusive sense. Unlike the exclusive "or" that we sometimes use in common language (as in "either you come or you stay"), the logical disjunction ∨ does not exclude the possibility that both conditions are met simultaneously.
Let's look at some examples to understand inclusive disjunction:
- "To pass the course, the student must submit the final project or take the make-up exam.” In this proposition, we see how the inclusive "or" works, since if a student only submits the project, they pass. If they only take the exam, they pass. And, if they do both, they also pass.
- "To enter the event, you need an invitation or to be a member of the club." Fulfilling just one condition (having an invitation or being a member) is sufficient to enter. If a person meets both conditions, they are also permitted.
- If p is "it is hot" and q is "it is humid," then p ∨ q means "it is hot or it is humid," understanding that this statement is true if one or the other phenomenon occurs, or both.
- If p is "2 is an even number" (true) and q is "2 is a prime number" (true), then p ∨ q: "2 is an even number or it is prime" is true, since both component propositions are true.
A practical way to distinguish it from other connectives is to remember that the symbol ∨ resembles a "V" (from "vel," the Latin word for "or"), with the point facing down. It should not be confused with the symbol for conjunction ∧ ("and"), which has its point facing up.
There is another type of disjunction called exclusive disjunction, strong disjunction, or symmetric difference. Its symbol is ⊻ and it differs from the inclusive one because it is true only when one of the propositions that compose it is true, and it is false if both are true or both are false. In this article, we will only discuss the first type of disjunction, the inclusive one.
Table of Contents
Truth table
As we said before, the disjunction is true when at least one of the propositions that compose it is true (or both are) and is false when both are false. This behavior is best visualized with a truth table:
| p | q | p ∨ q |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
For example, the compound proposition "it is hot or it is humid, or both" is true when it is true that it is hot, that it is humid, or both at the same time; it is false when neither part is true. The statement "2 is an even number or it is prime" is true because both propositions are true: 2 is even and is also prime.
The expression "a triangle has three sides or a square has seven" is true because triangles do have three sides, even though squares do not have seven. Since one of the components is true, the disjunction is true. In contrast, the proposition "2+2=5 or 2+2=9" is a false disjunction because it is not true that 2+2=5, nor is it true that 2+2=9.
Properties
Inclusive disjunction satisfies a series of properties that are essential for manipulating and simplifying propositional formulas. We see them below.
1) Commutativity: the order of the propositions does not affect the truth value of the disjunction.
p ∨ q ≡ q ∨ p
2) Associativity: the grouping of the propositions does not affect the truth value of the disjunction.
(p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
3) Idempotence: disjuncting a proposition with itself provides no new information; the result is logically equivalent to the original proposition.
(p ∨ p) ≡ p
4) Distributivity: disjunction distributes over conjunction and vice versa.
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
5) Identity or neutral element: when any proposition is disjuncted with a contradiction (an always false proposition, F), the result is equivalent to the original proposition. The falsehood does not contribute to the truth of the disjunction.
(p ∨ F) ≡ p
6) Dominant or absorbent element: when any proposition is disjuncted with a tautology (an always true proposition, T), the result is always true, regardless of the value of p. The tautology "dominates" the operation.
(p ∨ T) ≡ T
7) Complementation (law of the excluded middle): when a proposition is disjuncted with its negation, the result is a tautology (always true).
(p ∨ ¬p) ≡ T
8) Negation of disjunction (De Morgan's Law): the negation of a disjunction is equivalent to the conjunction of the negations.
¬(p ∨ q) ≡ ¬p ∧ ¬q
9) Absorption: this law shows how a disjunction can be "absorbed" or simplified when one of its components interacts with a conjunction.
p ∨ (p ∧ q) ≡ p
10) Disjunction elimination (disjunctive syllogism): this is an inference rule that allows us to derive a conclusion from a disjunction and the negation of one of its components.
[(p ∨ q) ∧ ¬p] → q
[(p ∨ q) ∧ ¬q] → p
Disjunction in set theory
In set theory, inclusive disjunction finds its direct equivalent in the union of sets: an operation that combines two or more sets to form a new one containing all the elements that belong to any of the original sets.
The union of two sets A and B, denoted as A ∪ B, is formally defined as:
A ∪ B = { x | x ∈ A ∨ x ∈ B }
This definition explicitly uses the inclusive disjunction operator (∨). The element x belongs to the union if it is in A, in B, or in both.
Let's look at some concrete examples of this operation:
- Given the sets A = {1, 3, 5} and B = {2, 3, 4}, their union is A ∪ B = {1, 2, 3, 4, 5}. We note that element 3, which belongs to both sets, appears only once in the result, as a set does not allow duplicate elements.
- If we define C as the set of vowels {a, e, i, o, u} and D as the first letters of the alphabet {a, b, c}, the union C ∪ D results in {a, b, c, e, i, o, u}.
- Consider the set of positive even numbers P = {2, 4, 6, ...} and the set of positive odd numbers I = {1, 3, 5, ...}. Their union P ∪ I is equal to the set of all positive natural numbers, which shows that two disjoint sets (with no common elements) can be joined to form a single one.
The union of sets, like its logical counterpart, satisfies a series of fundamental properties:
- Commutativity: A ∪ B = B ∪ A.
- Associativity: (A ∪ B) ∪ C = A ∪ (B ∪ C).
- Distributivity over intersection: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
- Idempotence: A ∪ A = A.
- Identity element: A ∪ ∅ = A (∅ is the empty set).
- Dominant element: A ∪ U = U (U is the universal set).
- Complement law: A ∪ A' = U (A’ is the complement of A).
Disjunction in a logic circuit
In the field of digital electronics and computer architecture, inclusive disjunction is physically embodied in a fundamental component: the OR logic gate. This gate receives one or more input signals (usually two) and produces a single output.
Its operation is based on a simple principle: the output will be 1 (true or "high") if at least one of its inputs is 1. If all inputs are 0 (false or "low"), the output will be 0. This behavior is represented in a truth table:
| Input A | Input B | Output (A OR B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
In most programming languages, inclusive disjunction is represented by the || operator (as in C, Java, JavaScript). For example, in a condition like if (isRaining || isCold), the code block will execute if at least one of the two events occurs, or both. Some languages, such as Python or SQL, also use the word OR.
Leave a Reply

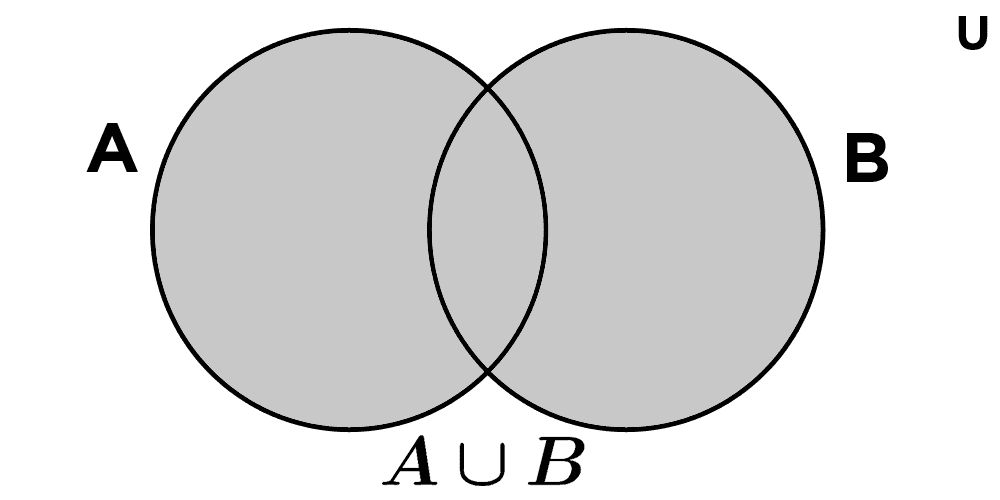
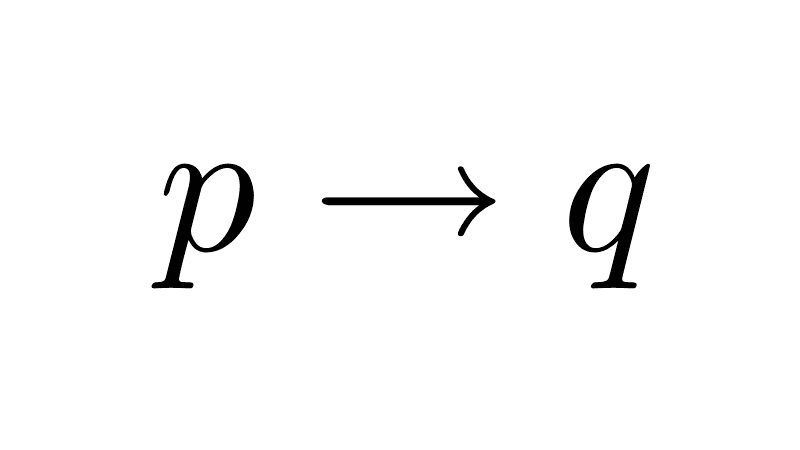
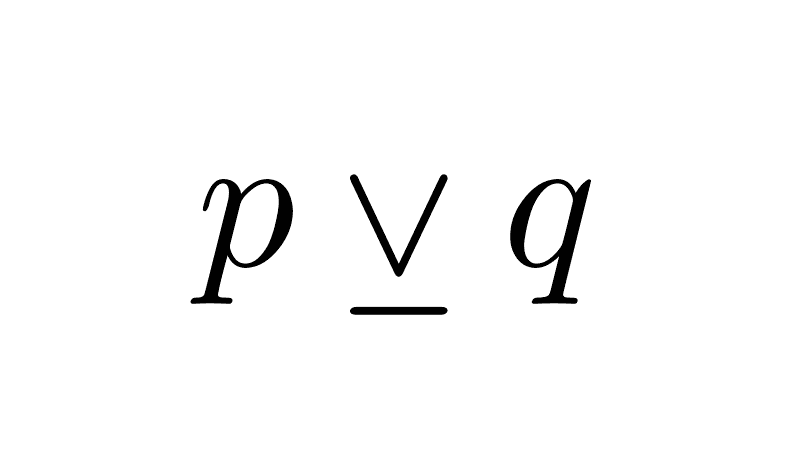

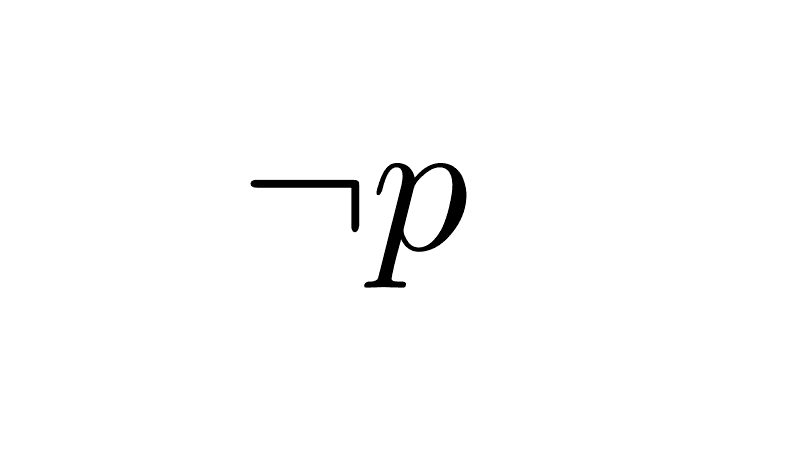
Related posts