Real Numbers

A real number is a type of number that corresponds to a point on the number line. Real numbers include rational numbers, which can be written as a fraction, and also irrational numbers, which cannot be expressed as a fraction. Some examples are: -2, 5, 3/2, π, √2, ∛7, 0, -5/4.

Set of real numbers

The set of real numbers is symbolized by the letter R and is equal to the union of the sets of rational and irrational numbers:

*\mathbb{R}=\mathbb{Q}\cup\mathbb{I}*

Another way to express the set of real numbers is by using the interval ranging from negative infinity to positive infinity: *\mathbb{R}=(-\infty, +\infty)*

Real numbers are used in various areas of science and mathematics, especially in expressing continuous quantities like length and time. The ability to accurately represent continuous quantities makes real numbers fundamental in these fields.

All natural, integer, rational, irrational, and decimal numbers are real numbers. This becomes clearer in the following diagram, where we can see all the numbers that make up the set of real numbers.

We then have two types of real numbers: rational numbers and irrational numbers. In addition to what is shown in the diagram, other examples of real numbers are:

*-27;~~\sqrt[3]{8};* *~~-\dfrac{\sqrt{2}}{2};~~\dfrac{\pi}{9};* *~~\dfrac{e^7}{\sqrt{3}};~~3,17897546;* *~~2,645751311...*

Every real number can be written in decimal form. These decimal representations can be terminating or non-terminating. In the case of terminating decimal representations, the decimal part has a limited number of digits after the decimal point and eventually ends. For example, the number 3.25 is a terminating decimal, as it has only two digits after the decimal point and then stops.

On the other hand, non-terminating decimal representations can be repeating or non-repeating.

• Repeating decimals follow a repetitive pattern of digits after the decimal point. For example, the number 1/3 has a repeating decimal representation: 0.333..., where the "3" repeats infinitely. The number 47/11 in decimal form is 4.27272..., where "27" repeats constantly. The three dots at the end indicate that there are more digits that are not written.
• Non-repeating decimals do not follow a repetitive pattern, and the digits after the decimal point continue infinitely without a pattern. For example, the number π (pi) has a non-repeating decimal representation: 3.14159265358979…

All terminating and repeating infinite decimals are rational numbers, whereas non-repeating infinite decimals are irrational numbers.

Properties of real numbers

The properties of the set of real numbers are:

1. It is an infinite set: The real numbers form an infinite set, meaning there is an unlimited quantity of real numbers.
2. It has no first or last element: There is no real number that is the smallest of all, nor one that is the largest.
3. It is a dense and complete set: Between any pair of distinct real numbers, there are infinitely many real numbers. Completeness implies that there are no "gaps" on the real number line.
4. It is a continuous set: Related to the above, the continuity of real numbers means there are no "jumps" on the real number line; that is, there are no holes or gaps between real numbers.
5. It is a totally ordered set: Real numbers can be ordered according to their magnitude. This means that for any pair of real numbers, one is greater than the other, or they are equal.

The real number line

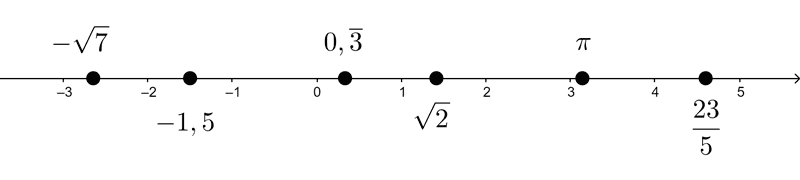
The set of real numbers can be represented by a line, called the real number line. Each point on this line represents a real number, and each real number corresponds to a unique point on the line. This is called a one-to-one correspondence. For this reason, real numbers complete the number line.

On a line, we first choose an arbitrary point called the origin and associate it with the number zero. By convention, we place positive real numbers to the right of zero and negative ones to the left. Zero is neither positive nor negative. The arrow pointing to the right indicates that the numbers increase in that direction.

Given two distinct real numbers, the one further to the right will be greater, and similarly, the one further to the left will be smaller. For example, from the graph, we can see that π is greater than √2, and at the same time, π is less than 23 / 5.

Operations on Real Numbers

The set of real numbers along with the operations of addition and multiplication is called the real number system. The rules of algebra for this system allow us to express mathematical facts in simple and concise forms and to solve equations to find answers to mathematical questions.

Below, we state the basic properties of the real number system with respect to the operations of addition and multiplication. The letters a, b, c represent real numbers.

Property	Description	Symbolic Representation
Closure Property	When addition and multiplication operations are performed with real numbers, the results are also real numbers.	a + b is a real number ab is a real number
Associative Property	The sum of three real numbers can be obtained by grouping the addends in one of two ways, and the product of three real numbers can be determined by grouping the factors in one of two ways.	a + (b + c) = (a + b) + c a(bc) = (ab)c
Commutative Property	The sum and product of two real numbers are not affected by the order of the numbers.	a + b = b + a ab = ba
Distributive Property	The product is distributive with respect to the sum of real numbers.	a (b + c) = ab + ac
Existence of Identity Elements	0 is the additive identity and 1 is the multiplicative identity.	a + 0 = a a ⋅ 1 = a
Existence of Additive Inverse	Every real number a has an additive inverse, which is -a.	a + (-a) = 0
Existence of Multiplicative Inverse	Every non-zero real number a has a multiplicative inverse, which is 1/a, also denoted as a-1.	a ⋅ a-1 = 1
Zero-Product Property	Multiplying any real number by zero results in zero.	a ⋅ 0 = 0 ⋅ a = 0 If ab = 0, then a = 0 or b = 0 (or both).
Cancellation Property	If the same number is added to or multiplied by both sides of an equality and the result does not change, that number can be “canceled”.	If a + c = b + c, then a = b If ac = bc and c ≠ 0, then a = b
Multiplication with Negative Numbers	The following properties relate to the negative sign in multiplication.	-(-a) = a -(ab) = (-a) b = a (-b) -a = (-1) a (-a) (-b) = ab

Sign of a Real Number

We can identify two major subsets of real numbers, which are:

• Positive real numbers, denoted as *\mathbb{R}^{+}*
• Negative real numbers, denoted as *\mathbb{R}^{-}*

We refer to the sign of a real number as positive if the number is positive, or negative if the number is negative. Two real numbers have the same sign if both are positive or both are negative. Two numbers have opposite or different signs if one is positive and the other is negative.

The following results about the signs of products and quotients of two real numbers a and b can be proven using properties of negatives and quotients.

Examples

Let *a=7* and *b=-24.* Since they have different signs, the product and quotient of these numbers will be negative:

*7\cdot (-24)=-168* is negative.

*\dfrac{7}{-24}=-\dfrac{7}{24}* is negative.

The same can be shown by taking numbers with the same sign.

It is important to recognize the difference between a negative real number and the negative of a real number. In particular, the negative of a real number a can be positive. For example, if a is negative, say a = -5, then its negative -a = -(-5) = 5 is positive. In general, we have the following relationships:

• If a is positive, then -a is negative.
• If a is negative, then -a is positive.

Order Relation in Real Numbers

In the following table, we define the notions of greater than and less than for real numbers a and b. The symbols < and > are inequality signs, and the expressions a > b and a < b are called inequalities.

Notation	Definition	Terminology
a > b	a - b is positive	a is greater than b
a < b	a - b is negative	a is less than b

Examples

• 5 > 3 because 5 - 3 = 2 is positive.
• 9 < 10 because 9 - 10 = -1 is negative.
• -4 < -1 because -4 - (-1) = -3 is negative.
• -6 < 1 because -6 - 1 = -7 is negative.

The law we see next allows us to compare any two real numbers.

An expression of the form a < b < c is called a continued inequality and means that a < b and b < c; we say "b is between a and c". Similarly, the expression c > b > a means that c > b and b > a.

The notation a ≥ b is read "a is greater than or equal to b" and means that a > b or a = b (but not both). The symbol a ≤ b is read "a is less than or equal to b", and it means that a < b or a = b. Expressions of the form a ≥ b and a ≤ b are called non-strict inequalities, because a can be equal to b.

Limitations of Real Numbers

Real numbers are a fundamental set in mathematics, but they have limitations. The main one is that there is no real solution for the square root of a negative number. This limitation extends to all even-indexed roots of negative numbers. For example, *\sqrt{-1}* is not a real number, as no real number squared results in a negative number. An equation like *x^2+2=0* also has no solution in this number set, because solving for x leads to the expression *x=\sqrt{-2}.*

To overcome this limitation, the concept of complex numbers is introduced. They are an extension of the set of real numbers and are defined as numbers that include both a real part and an imaginary part. With them, it becomes possible to find the square root (or any even-indexed root) of negative numbers.