
Irrational Numbers
Irrational numbers are real numbers that cannot be expressed as a fraction, that is, they cannot be written as a quotient of integers. In other words, irrational numbers cannot be written in the form a/b where a and b are integers and b ≠ 0. Examples of irrational numbers are: π, ϕ, e, √2, √3, √5, ∛2, π2, -∛5, -2e.
The word "irrational" comes from the Latin "irrationalis," which means "without reason" or "without ratio." The main characteristic of irrational numbers is that their decimal expansion is infinite and non-repeating. This distinguishes them from rational numbers, which in their decimal form have either a finite number of digits or an infinite number where a group of digits repeats constantly.
Table of Contents
Why Do Irrational Numbers Arise?
Irrational numbers arise as a natural consequence of the need to express quantities that cannot be represented as fractions. For example, rational numbers cannot be used to express the solutions to the equation x2=2, as no rational number squared results in 2. The positive solution to this equation is the so-called square root of 2, which we can approximate as:
*\sqrt{2}=1.41421356237309…*
We could calculate more decimal places, but we would never finish. Furthermore, there are no digits that repeat periodically. This indicates that the square root of 2 is an irrational number.
The existence of irrational numbers was a surprising discovery in the history of mathematics, as it contradicted the ancient belief that all numbers could be expressed as fractions.
Irrational numbers have a significant presence in geometry, especially in the measurement of lengths, areas, and volumes. For example, the value of π (a well-known irrational number) appears in formulas for calculating the circumference and area of a circle.
The Set of Irrational Numbers
The set of all numbers that cannot be written as a fraction is called the set of irrational numbers, and it is symbolized by the letter I.
*I=\{x |* x cannot be written as a/b where a and b are integers and b≠0 *\}*
or also, *I=\{x |* the decimal representation of x is neither terminating nor repeating *\}*
All irrational numbers are real numbers, but not all real numbers are irrational. If a number is irrational, then it cannot be a natural, integer, or, obviously, a rational number, but it is a real number.
The set of irrational numbers is infinite and uncountable, which means there is an infinite quantity of irrational numbers between any pair of real numbers.
Examples of Irrational Numbers
Some irrational numbers we can mention are:
- The roots of natural numbers whose results are not natural numbers. Examples: *\sqrt{5},\sqrt{11}, \sqrt{17}, \sqrt{26},...*
- The roots of integers whose results are not integers. Examples: *\sqrt[3]{3},\sqrt[7]{-21},\sqrt[5]{-14},...*
- The roots of rational numbers whose results are not rational numbers. *\sqrt[2]{\dfrac{1}{2}}, \sqrt[3]{-\dfrac{1}{3}}, \sqrt{0.75},...*
- Numbers obtained by combining infinite decimal digits without periodicity. For example: *0.010010001..., 0.020020002…*
- Numbers that arise from geometry or other branches of mathematics: *\pi, \phi, e, e^2, \pi+1,* we will discuss these numbers later.
To obtain an irrational number, it is sufficient to write a number whose decimal digits are infinite and non-repeating. For example: 3.515511555111...
The irrationality of certain numbers can be demonstrated using methods such as proof by contradiction or geometric arguments. The values of irrational numbers can be approximated on a scientific calculator.
Important: any real number a can be written in the form a/1. However, the fact that this representation is possible does not mean the number is rational. √2 / 1 is an irrational number, even though it seems like it can be written as a fraction. Remember that for it to be a fraction, both the numerator and the denominator must be integers.
Classification of Irrational Numbers
Irrational numbers are divided into two types: algebraic irrationals and transcendental irrationals.
Algebraic Irrationals
Algebraic irrational numbers are those that are solutions to polynomial equations with integer coefficients. That is, they are solutions to an equation of the form *a_n x^n+a_{n-1} x^{n-1}+...+a_1 x+a_0=0,* where *a_n, a_{n-1},...,a_1,a_0* are integers and n is a natural number. Algebraic irrationals can be expressed algebraically in terms of sums, subtractions, multiplications, divisions, and roots of integers.
All non-exact roots of any index are algebraic irrationals. For example: *\sqrt{2}, \sqrt{3}, \sqrt[3]{7}, -\sqrt[4]{13}, etc.* The square root of 2 is a solution to the equation *x^2-2=0,* the cube root of 3 is a solution to *x^3-3=0,* and so on for any non-exact radical expression. The golden ratio *\phi* is an algebraic irrational, as it can be written as *\phi=\dfrac{1+\sqrt{5}}{2}*
Transcendental Irrationals
Transcendental irrational numbers are those that are not solutions to polynomial equations with integer coefficients, which means they cannot be expressed algebraically in terms of sums, subtractions, multiplications, divisions, and roots of integers. Some well-known examples of transcendental irrational numbers are π and e.
Famous Irrational Numbers
There are three very well-known irrational numbers in mathematics and other sciences: π (pi), ϕ (phi), and e (or Euler's number).
Number π
Pi is a fundamental irrational number in mathematics that represents the ratio of a circle's circumference to its diameter. Its approximate value is:
*\pi=3.14159265...*
Since antiquity, it has fascinated mathematicians and scientists, and its study continues to be relevant in various areas, including geometry, physics, and computer science.
Given a circle with circumference C and diameter d, the following relationship holds:
*\dfrac{C}{d}=\pi*
That is, a circle's diameter fits into its circumference *\pi* times.
Number ϕ
The number phi, also known as the golden number, golden mean, or the golden ratio, is an irrational number whose approximate value is:
*\phi=1.6180339887...*
This number is the positive solution to the quadratic equation *x^2=x+1,* and can be written as:
*\phi=\dfrac{1+\sqrt{5}}{2}*
The number phi is notable for its presence in nature and art, as it is found in the arrangement of petals in many flowers, in the architecture of famous buildings like the Parthenon, and in other aesthetic manifestations. It is a symbol of harmony and beauty, and its study has been central in fields such as geometry, art, and number theory.
Number e
The number e, also called Euler's number, is another fundamental irrational in mathematics. It is the base of natural logarithms and arises in various areas such as probability, statistics, calculus, and physics.
*e=2.71828182845904...*
The number e can also be defined as the value that the expression *\left(1+\dfrac{1}{x}\right)^x* approaches as *x* becomes very large. Symbolically, this is expressed as:
*e=\lim_{x\to \infty}\left(1+\dfrac{1}{x}\right)^x*
Euler's number is also the base of the natural exponential function ex, which plays a crucial role in the study of phenomena that exhibit exponential growth, such as compound interest, population growth, and other applications in natural and social sciences.
Representation on the Number Line
Rational numbers are not able to complete the number line without leaving gaps. These gaps are filled by the irrational numbers. Between any two rational numbers, there are infinitely many irrational numbers.
Operations with Irrational Numbers
The operations that can be performed between irrational numbers are the same as those that can be done with any real number. These operations include addition, subtraction, multiplication, and division. Furthermore, the properties of these operations continue to hold:
- Associativity: The order in which numbers are grouped in addition and multiplication does not affect the final result.
- Commutativity: The order in which numbers are added or multiplied does not affect the final result.
- Identity element: For addition, the identity element is 0, which means that adding it to any number does not alter the original value. Example: √5+0=√5. For multiplication, the identity element is 1, with an analogous result to addition, for example, π ⋅ 1=π.
- Inverse element: The sum of an irrational number and its additive inverse (the negative of the number) is zero, for example, ∛6+(-∛6)=0. The product of an irrational number a and its multiplicative inverse 1/a is one, for example, √3 ⋅ 1/√3 = 1.
- Distributivity: This property states that multiplication distributes over addition. For example: e (π+√2) = eπ + e√2.
Usually, when we talk about operating with irrational numbers, we are referring to working with radical expressions, that is, those involving square roots, cube roots, or other roots of numbers.
Properties of Irrational Numbers
Operations with irrationals also follow the properties below.
- The sum or product of two irrational numbers can result in either a rational or an irrational number.
- The sum or difference of a rational and an irrational number results in an irrational number.
- The product of a non-zero rational number and an irrational number results in an irrational number.
- The quotient of a non-zero rational number and an irrational number results in an irrational number.
- The multiplicative inverse of an irrational number is another irrational number.
Leave a Reply

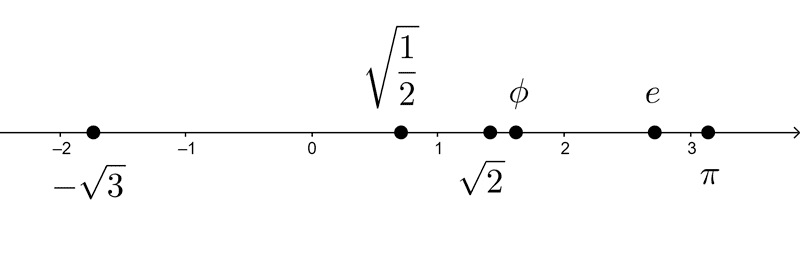



Related posts