
Number sets
Number sets are groups or collections of numbers organized according to their common mathematical properties. Each set has its own definition and properties that distinguish it from the others, allowing for a precise and effective approach to a variety of mathematical situations and problems.
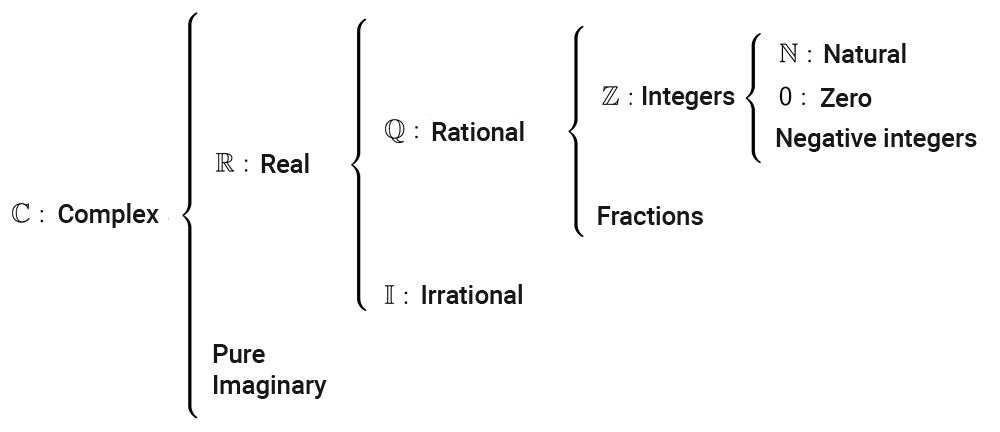
There are six fundamental number sets, which are: natural numbers (N), integers (Z), rational numbers (Q), irrational numbers (I), real numbers (R), and complex numbers (C). Throughout the historical development of mathematics, to overcome the limitations of a number set, other classes of numbers were successively introduced that allowed new problems to be solved. You can learn the definition and characteristics of each by visiting the corresponding article:
Table of Contents
Diagram of Number Sets
Number sets can be diagrammed as follows.
Natural Numbers
The natural numbers are the elements of the sequence 1, 2, 3, 4, … and were the first to be used by ancient civilizations for counting objects and representing quantities. Each one has a successor that is one unit greater; for example, the successor of 12 is 12 + 1 = 13.
The set of natural numbers is symbolized by the letter N:
$$ \mathbb{N}=\{1, 2, 3, 4, 5, …\} $$
Natural numbers are used for counting objects and representing discrete quantities; for instance, they are used to count the number of people at a meeting or the total elements in a set. They also allow for establishing a sequential order; for example, they can be used to number positions in a competition or stages in a process.
The number zero is sometimes considered a natural number, as it is necessary to mark the absence of elements to count. For instance, to express that there are no students in a classroom, one could say there are zero students. When zero is included with the natural numbers, we form the set of whole numbers, which is denoted by adding a subscript to the set symbol:
$$ \mathbb{N}_0=\{0, 1, 2, 3, 4, 5, …\} $$
Some examples of natural numbers are: 66, 210, 15, 50, 92, 103, 245. All natural numbers are positive (or non-negative if zero is included).
In this set, we can define the arithmetic operations of addition, subtraction, multiplication, division, exponentiation, and root extraction. We will consider zero as a natural number for the following properties.
The most important properties of the set of natural numbers are:
- It is infinite and ordered.
- It has a first element, but no last element.
- Every natural number has a successor.
- Between any two distinct natural numbers, there is a finite number of natural numbers.
Limitations of Natural Numbers
The set of natural numbers is limited in the sense that some operations cannot be performed with any two natural numbers, as the result may not be a natural number. For example:
- When subtracting two natural numbers, the minuend cannot be smaller than the subtrahend.
- Exact division cannot be performed if the dividend is not a multiple of the divisor.
- The nth root of a natural number cannot be extracted if the number is not itself the nth power of a natural number.
Division by zero is also forbidden, but this is not unique to natural numbers; it occurs in all number sets.
Integers
There are everyday expressions that cannot be indicated with natural numbers. For these, it is necessary to use negative numbers:
- When talking about temperatures below zero. For example, 5 °C below zero is expressed as -5 °C.
- When discussing debts. For example, if we owe $500, we say our balance is -$500.
- When referring to the floors of a building. Example: the basement is floor -1.
The integers arise as a solution to the limitation of natural numbers regarding subtraction. Introducing negative numbers -1, -2, -3, … allows the subtraction operation a - b to be performed even when a is less than b. We integrate negative numbers and zero with natural numbers to form a new number set.
The set of integers is represented by the letter Z and consists of the natural numbers (1, 2, 3, 4, ...), negative numbers (-1, -2, -3, -4, ...), and zero (0).
$$\mathbb{Z}=\{…, -4, -3, -2, -1, 0, 1, 2, 3, 4, … \}$$
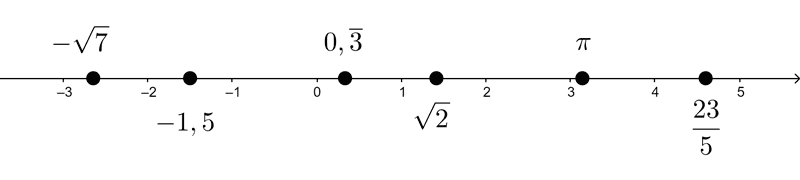
Some examples of integers are: -40, 2, 0, 27, -34, 18.

Operations with integers are defined so that whenever they involve positive numbers, the definitions and properties of natural numbers are preserved. Thus, to add two integers, if both have the same sign, that sign is used, and the corresponding natural numbers are added. If they have different signs, the sign of the larger number is prefixed, and the smaller is subtracted from the larger. For multiplication and division, the rule of signs is adopted: factors with the same sign yield a positive product, and factors with different signs yield a negative product.
The most important properties of the set of integers are:
- It is infinite and ordered.
- It has neither a first nor a last element.
- Every integer has a successor.
- Between any two distinct integers, there is a finite number of integers.
Limitations of Integers
When performing additions, subtractions, or multiplications with integers, the result is always an integer. However, we still retain some limitations from the natural numbers and encounter a new one:
- Exact division cannot be performed if the dividend is not a multiple of the divisor.
- The nth root of an integer cannot be extracted unless it is the nth power of an integer. Furthermore, even-indexed roots of negative numbers do not exist.
Subsets of Integers
From the set of integers, we can define a series of subsets:
- Positive integers *\mathbb{Z}^+:* all the natural numbers. *\mathbb{Z}^+=\{1,2,3,4,...\}.*
- Negative integers *\mathbb{Z}^-:* all negative numbers, opposites of the natural numbers. *\mathbb{Z}^-=\{-1,-2,-3,-4,...\}.*
- Non-negative integers *\mathbb{Z}^{+}_0:* all positive integers plus zero. *\mathbb{Z}^{+}_0=\{0,1,2,3,4,5,...\}.*
- Non-positive integers *\mathbb{Z}^{-}_0:* all negative integers plus zero. *\mathbb{Z}^{+}_0=\{0,-1,-2,-3,-4,-5,...\}.*
- Integers except zero: *\mathbb{Z}^{*}=\{-2,-1,1,2,3,...\}*
Note: These subset notations are maintained in the following number sets up to the real numbers. To indicate positive numbers, a + superscript is added to the set symbol; for negative numbers, a - superscript is used; to indicate the inclusion of zero, a 0 subscript is used; to indicate the exclusion of zero, an asterisk superscript is used.
Rational Numbers
The introduction of fractional numbers a / b allows for exact quotients a ÷ b between integers, even in cases where a is not a multiple of b. The integer a is called the numerator, and the integer b, which cannot be 0, is called the denominator.
Integers and fractional numbers together form the set of rational numbers, which we symbolize with the letter Q:
$$ \mathbb{Q}=\left\{\frac{a}{b}~\text{such that a and b are integers and b is not zero}\right\} $$
Fractional numbers serve, among other things, to represent parts of a whole quantity; for example, 1/4 of a cake means one piece of a cake divided into 4 equal parts. Fractions are also essential for expressing proportions and rates, such as interest rates, growth percentages, and ratios between quantities.
Some examples of rational numbers are: 1/2, 3/4, -5/3, 27/7.
The most important properties of the set of rational numbers are as follows:
- It is infinite and ordered.
- It has neither a first nor a last element.
- Between any two distinct rational numbers, there are infinitely many rational numbers.
An integer can be written as a fraction with a denominator of 1, which allows us to say that every integer is a rational number. Before defining operations between fractions, we will emphasize the property of equality:
*\dfrac{a}{b}=\dfrac{c}{d}* if and only if *ad=bc*
This relationship tells us that two fractional numbers are equal if their cross-products are equal. Two fractions that satisfy this condition are called equivalent fractions. For example, *1/2* is equivalent to *6/12,* because *1\cdot 12=2\cdot 6.*
To obtain a fraction equivalent to a given fraction, we can multiply the numerator and the denominator by the same integer. We can also divide the numerator and denominator by the same integer, as long as it is a divisor of both.
Operations with Rational Numbers
*\dfrac{a}{b}+\dfrac{c}{d}=\dfrac{ad+bc}{bd}*
*\dfrac{a}{b}-\dfrac{c}{d}=\dfrac{ad-bc}{bd}*
*\dfrac{a}{b}\cdot \dfrac{c}{d}=\dfrac{a\cdot c}{b\cdot d}*
*\dfrac{a}{b}:\dfrac{c}{d}=\dfrac{a}{b}\cdot \dfrac{d}{c}=\dfrac{a\cdot d}{b\cdot c}*
*\left(\dfrac{a}{b}\right)^n=\dfrac{a^n}{b^n}*
*\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}*
Limitations of Rational Numbers
When performing additions, subtractions, multiplications, and divisions (except division by zero) between rational numbers, the result is always a rational number. However, we still have a significant limitation:
- The nth root of a rational number cannot be extracted if it is not itself the nth power of a rational number. Also, even-indexed roots of negative numbers have no solution.
Subsets of Rational Numbers
Just as with integers, we can define a series of frequently used subsets.
- Positive rationals: *\mathbb{Q}^+=\left\{\dfrac{a}{b}~\text{such that}~\dfrac{a}{b}>0\right\}*
- Negative rationals: *\mathbb{Q}^-=\left\{\dfrac{a}{b}~\text{such that}~\dfrac{a}{b}<0\right\}*
- Non-negative rationals: *\mathbb{Q}^+_0=\left\{\dfrac{a}{b}~\text{such that}~\dfrac{a}{b}≥0\right\}*
- Non-positive rationals: *\mathbb{Q}^-_0=\left\{\dfrac{a}{b}~\text{such that}~\dfrac{a}{b}≤0\right\}*
- Rationals except zero: *\mathbb{Q}^{*}=\left\{\dfrac{a}{b}~\text{such that}~\dfrac{a}{b}≠0\right\}*
Decimal Numbers
Decimal numbers do not form a set in themselves but are a way of expressing numbers. Rational numbers are sometimes represented as decimals. For example, the numbers 3/4, 5/2, -2/3, and 7/66 can be represented as decimals simply by performing the division:
*\dfrac{3}{4}= 0.75*
*\dfrac{5}{2} = 2.5*
*-\dfrac{2}{3}=-0.6666… = -0. \overline{6}*
*\dfrac{7}{66}=0.1060606…=0.1 \overline{06}*
We observe that the decimal representation of 3/4 and 5/2 terminates or ends; these are called terminating decimals. The decimal representation of the other two numbers does not end, but a repeating pattern is visible. For -2/3, the 6 repeats indefinitely, as indicated by the bar over it; for 7/66, the block 06 repeats indefinitely, as indicated by the bar over 06. These last two are called repeating decimals.
It can be shown that every rational number can be represented by a decimal that either terminates or is repeating, and vice versa.
Irrational Numbers
There are numbers whose decimal expression does not fall into either of the two categories mentioned above; that is, they are neither terminating nor repeating decimals, but have infinite decimal places that do not follow any pattern.
These numbers cannot be written as fractions and, therefore, are not rational. They are another type of number, called irrational numbers. In other words, irrational numbers are those that cannot be written as a fraction a / b, where a and b are integers and b is not zero.
The set of irrational numbers is symbolized by the letter I:
*\mathbb{I}=\{x~\text{such that x cannot be written as a fraction}\}*
Irrational numbers arise naturally. For example, if we consider an isosceles right triangle whose legs have a length of 1, the hypotenuse measures *\sqrt{2}*, an irrational number.
Some famous irrational numbers are:
- *π=3.14159265…* which represents the ratio of a circle's circumference to its diameter.
- *e=2.71828182…* the base of natural logarithms.
- *ϕ=1.61803399…* the golden ratio.
Real Numbers
So far, we have two major groups of numbers: rationals and irrationals. The first can be written as fractions and include integers and natural numbers; the second group contains all numbers that cannot be written as fractions.
By joining rational and irrational numbers into a single set, we form the set of real numbers, which is symbolized by the letter R:
*\mathbb{R}=\mathbb{Q}\cup \mathbb{I}*
Real numbers allow us to solve roots that were not possible with rational numbers, for example: *\sqrt{2},~~\sqrt{\dfrac{5}{3}},~~\sqrt[3]{7}* are real numbers.
The most important properties of the set of real numbers are:
- It is infinite and ordered.
- It has neither a first nor a last element.
- Between any two distinct real numbers, there are infinitely many real numbers.
If a, b, and c are real numbers, addition has the following properties.
- Commutative property: *a+b=b+a*
- Associative property: *a+(b+c)=(a+b)+c*
- Identity element: is zero, *a+0=a*
- Inverse element: the inverse of *a* is *-a,* since *a+(-a)=0.*
If a, b, and c are real numbers, multiplication has the following properties.
- Commutative property: *ab=ba*
- Associative property: *a(bc)=(ab)c*
- Identity element: is one, *a\cdot 1=a*
- Inverse element: for every *a≠0,* its inverse is *1/a,* since *a\cdot \dfrac{1}{a}=1.*
- Distributive property: *a(b±c)=ab±ac*
- Multiplication by zero: if *ab=0,* then *a=0* or *b=0* (or both).
Limitations of Real Numbers
Integers solved subtractions where the minuend is smaller than the subtrahend. With the introduction of rational numbers, we solved divisions that did not yield integer results. Now, with real numbers, which include both rationals and irrationals, we solve a problem with nth roots, as it is no longer necessary for the radicand to be an nth power for the result to belong to the same set.
However, there is still a limitation related to roots: even-indexed roots of negative numbers cannot be extracted. For example, *\sqrt{-16}* has no solution in the set of real numbers, as there is no real number that, when squared, equals -16. To overcome this limitation, we move on to the final number set.
Subsets of Real Numbers
- Positive reals: *\mathbb{R}^+=\{x~\text{such that x is real and}~x>0\}*
- Negative reals: *\mathbb{R}^-=\{x~\text{such that x is real and}~x<0\}*
- Non-negative reals: *\mathbb{R}^+_0=\{x~\text{such that x is real and}~x≥0\}*
- Non-positive reals: *\mathbb{R}^-_0=\{x~\text{such that x is real and}~x≤0\}*
- Reals except zero: *\mathbb{R}^{*}=\{x~\text{such that x is real and}~x≠0\}*
Complex Numbers
To overcome the aforementioned restrictions, we introduce a new number set, which will include the real numbers and also allow for finding even-indexed roots of negative numbers. We start by defining a new number, called the imaginary unit and represented by the letter i, which has the following property:
*i^2=-1*
Note that i is not a real number, as no real number squared results in a negative number.
Numbers of the form *b\cdot i,* abbreviated as *bi,* where *b* is any real number, are called imaginary numbers, and binomials of the form *a+bi* where *a* and *b* are real, are called complex numbers. These complex numbers include real numbers as a special case (when b=0), and imaginary numbers (when a=0). If a=b=0, we have zero.
The set of all numbers corresponding to the form *a+bi,* where *a* and *b* are real numbers and *i^2=-1* is called the set of complex numbers and is symbolized by the letter C:
*\mathbb{C}=\{a+bi~~\text{such that a and b are real and}~~ i^2=-1\}*
In the complex number *a+bi,* the number *a* is called the real part, and the number *b,* the imaginary part. Two complex numbers are equal if their corresponding real and imaginary parts coincide.
*a+bi=c+di* if and only if *a=c* and *b=d*
An even-indexed root of a negative number can be rewritten and solved in this number set, keeping in mind that *i^2=-1.* For example:
*\sqrt{-4}=\sqrt{4\cdot (-1)}=\sqrt{4\cdot i^2}=\sqrt{4}\sqrt{i^2}=2i*
This result makes sense, since *(2i)^2=2^2\cdot i^2=4\cdot (-1)=-4*
With this in mind, the limitation of real numbers regarding even-indexed roots of negative numbers is overcome.
Complex numbers have various uses in both mathematics and science; they serve, among other things:
- To represent voltages, currents, and components in electrical circuits and control systems.
- To describe wave phenomena, such as the behavior of electromagnetic waves and oscillations in mechanical systems.
Addition of Complex Numbers
The sum of two complex numbers is another complex number where the real part is the sum of the real parts and the imaginary part is the sum of the imaginary parts.
*(a+bi)+(c+di)=(a+c)+(b+d)i*
Example:
*(2-4i) + (6+i)=*
*=(2+6) + (-4+1)i*
*=8-3i*
Multiplication of Complex Numbers
The multiplication of two complex numbers is performed as follows:
*(a+bi)(c+di)=(ac-bd)+(ad+bc)i*
It is not necessary to memorize the definition; we can simply use the distributive property, remembering that *i^2=-1*.
Example:
*(2+3i)(4-5i)=*
*=2\cdot 4+(2)(-5i)+(3i)(4)+(3i)(-5i)*
*= 8-10i+12i+(-3\cdot 5)i^2 *
*= 8+2i + (-15)(-1)*
*= 8+2i+15*
*= 23+2i*
According to these definitions, when adding or multiplying two complex numbers, the result will always be another complex number. It can also be shown that these operations are commutative and associative, and that multiplication is distributive over addition; that is, if *u, v, w* are complex numbers, then:
*u+v=v+u*
*uv=vu*
*(u+v)+w=u+(v+w)*
*(uv)w=u(vw)*
*u(v+w)=uv+uw*
Also, the identity element for addition is 0, which can be expressed as *0+0i.* The additive inverse of the complex number *a+bi* is the complex number *-a-bi,* since
*(a+bi)+(-a-bi)=[a+(-a)]+[b+(-b)]i=0+0i*
The multiplicative inverse (or reciprocal) of the complex number *a+bi* is defined as *\dfrac{1}{a+bi}.* Thus,
*(a+bi)\cdot \dfrac{1}{a+bi}=1*
Division of Complex Numbers
The division of complex numbers is performed by multiplying the numerator and denominator by the complex conjugate of the denominator, which is obtained by changing the sign of its imaginary part, and then carrying out the corresponding operations.
*\dfrac{a+bi}{c+di}=\dfrac{a+bi}{c+di}\cdot \dfrac{c-di}{c-di}*
For example:
*\dfrac{2+3i}{5-4i}=*
*=\dfrac{(2+3i)(5+4i)}{(5-4i)(5+4i)}*
*=\dfrac{10+8i+15i+12i^2}{5^2-(4i)^2} *
*=\dfrac{10+23i-12}{25-16i^2} *
*=\dfrac{-2+23i}{25+16} *
*=\dfrac{-2+23i}{41}*
In summary, by introducing complex numbers, we have overcome the limitation of real numbers, and with them, the "forbidden" operations are repealed, except for division by zero. One might then think of a new expansion of the number field that would allow this restriction to be lifted; but there is a theorem, called the final theorem of arithmetic, which asserts that the largest set of numbers that exists is that of complex numbers.
Leave a Reply







Related posts