
Set Operations
There are five set operations: union, intersection, difference, symmetric difference, and complement. Below, we will look at their definitions with solved examples for each.
Table of Contents
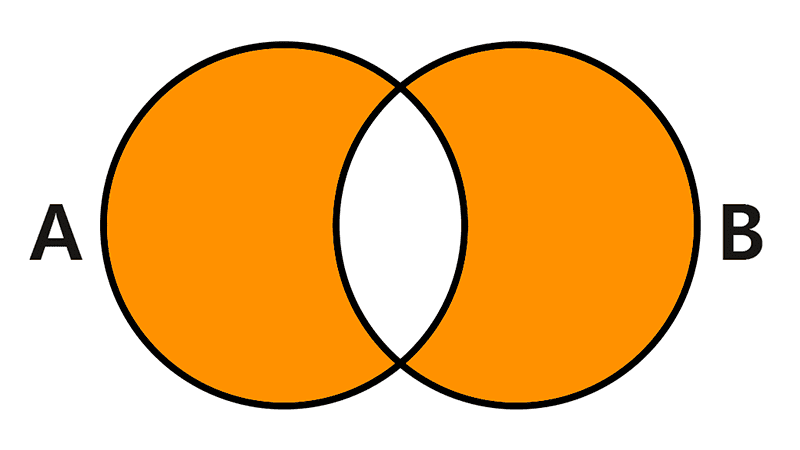
Union of sets
The union of A and B is the set formed by the elements of A or B or both. It is symbolized as A ∪ B and is read "A union B".
A ∪ B = {x | x ∈ A ∨ x ∈ B}
To calculate the union of two sets, we must combine the elements of both into a single set. For example:
If A = {1, 4, 6} and B = {7, 6, 9, 2}, then:
A ∪ B = {1, 2, 4, 6, 7, 9}
Note that if there are repeated elements, they are written only once in the union.
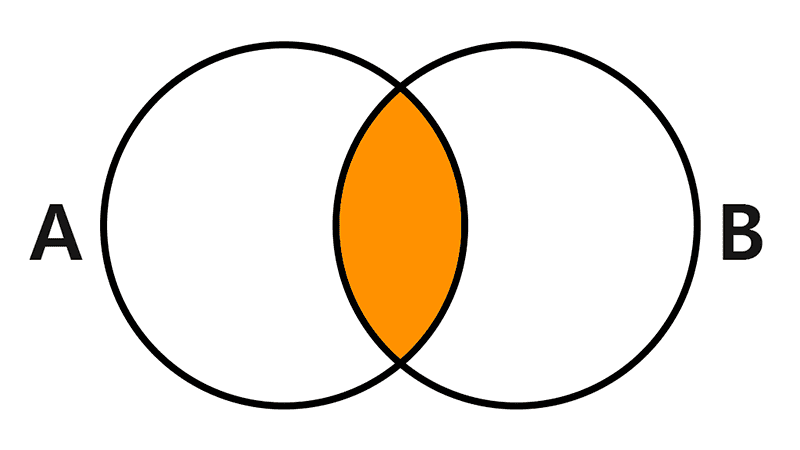
Intersection of sets
The intersection of A and B is the set formed by the elements that belong to both sets simultaneously. It is symbolized as A ∩ B and is read "A intersection B".
A ∩ B = {x | x ∈ A ∧ x ∈ B}
To calculate the intersection of two sets, we must look for the elements they have in common. For example:
If A = {1, 4, 6, 2} and B = {7, 6, 9, 2}, then:
A ∩ B = {2, 6}
If the sets have no elements in common, their intersection is the empty set, in which case the sets are said to be disjoint. For example, if C = {2, 5} and D = {3, 7}, then C ∩ D = ϕ.
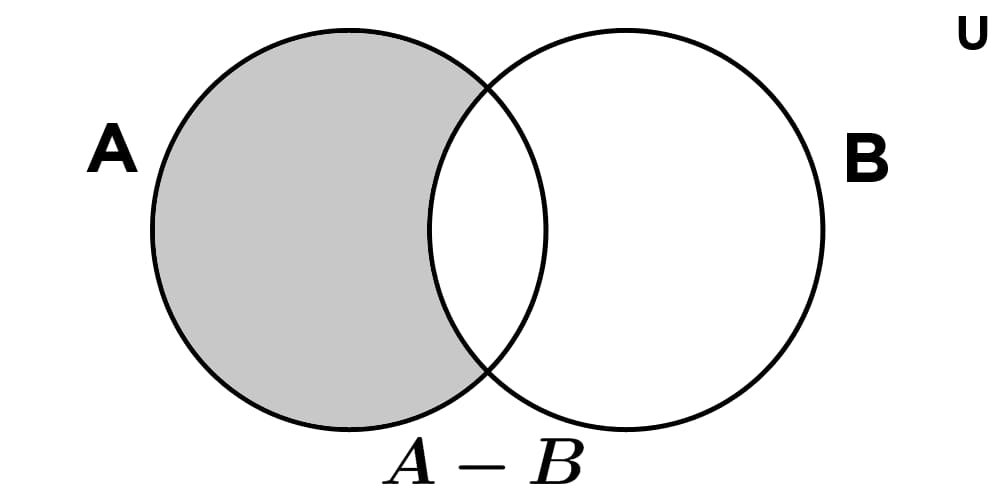
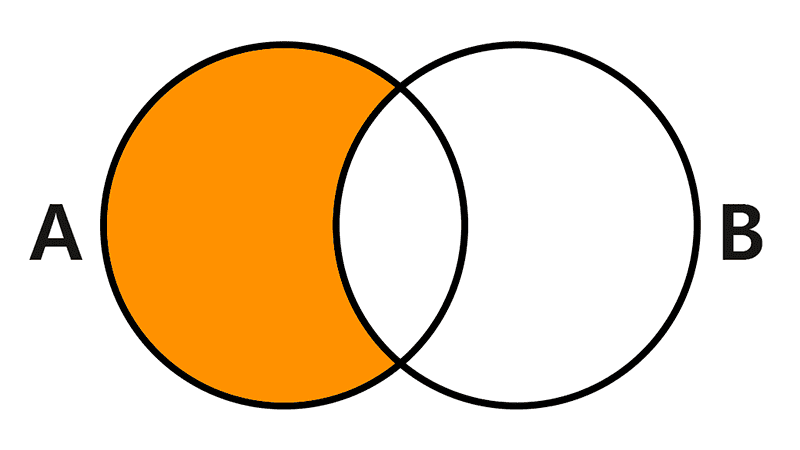
Difference of sets
The difference between two sets A and B is the set formed by the elements of the first set that do not belong to the second. It is symbolized as A - B and is read "A minus B".
A - B = {x | x ∈ A ∧ x ∉ B}
To calculate the difference between two sets, we must take the elements of the first set, excluding those it shares with the second. For example:
If A = {a, b, c, d} and B = {a, k, m}, then:
A - B = {b, c, d}
Symmetric difference of sets
The symmetric difference of two sets A and B, denoted by A Δ B, is the set of all elements that belong to either of the two sets, but not to both. In other words, it is the union of A - B and B - A:
A Δ B = (A - B) ∪ (B - A)
To calculate the symmetric difference of two sets, we must first calculate their differences and then unite them into a single set. For example:
Let A = {1, 4, 5} and B = {0, 4, 9}, we calculate:
A - B = {1, 5}
B - A = {0, 9}
With this, we get:
A Δ B = {1, 5, 0, 9}
Complement of a Set
We call the universal set, symbolized as U, the one that contains all the elements related to what we are working with. For example, if we are working with sets of letters like A = {c, d, e}, the universal set would be the one containing all the letters of the alphabet. If we work with sets of numbers, the set of real numbers is usually considered the universal set, unless otherwise indicated. In light of this, the following is defined:
The complement of a set A is the set whose elements belong to the universal set but do not belong to A. It is symbolized as CA, A', Ā, or Ac and is read "the complement of A".
Ac = {x | x ∈ U ∧ x ∉ A}
We can deduce that Ac = U - A
To calculate the complement of a set A, you must first know the universal set U, then exclude all elements of A from it. For example:
Let the universal set be U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and the set A = {1, 2, 3, 4}, the complement of A is:
Ac = {5, 6, 7, 8, 9, 10}
Properties of Operations
Next, we will see the most important properties of union, intersection, and complement. If A, B, and C are three sets, U is the universal set, and ϕ is the empty set, then the following laws hold:
| Property | Symbolic Form |
|---|---|
| Idempotent Laws | A ∪ A = A A ∩ A = A |
| Associative Laws | (A ∪ B) ∪ C = A ∪ (B ∪ C) (A ∩ B) ∩ C = A ∩ (B ∩ C) |
| Commutative Laws | A ∪ B = B ∪ A A ∩ B = B ∩ A |
| Distributive Laws | A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) |
| Identity Laws | A ∪ ϕ = A A ∩ U = A |
| Domination Laws | A ∪ U = U A ∩ ϕ = ϕ |
| Complement Laws | (Ac)c = A A ∪ Ac = U Ac = ϕ A ∩ Ac = ϕ ϕc = U |
| De Morgan's Laws | (A ∪ B)c = Ac ∩ Bc (A ∩ B)c = Ac ∪ Bc |
Practice Exercises
Exercise: Given the following sets:
U = { x | x is an integer between -3 and 10, inclusive }
A = {1, 3, 5, 7, 9}
B = {-3, -2, -1, 0, 1, 2, 3}
Find:
- A ∪ B
- A ∩ B
- A - B
- B - A
- A Δ B
- Ac
- Bc
Solutions:
- A ∪ B = {-3, -2, -1, 0, 1, 2, 3, 5, 7, 9}
- A ∩ B = {1, 3}
- A - B = {5, 7, 9}
- B - A = {-3, -2, -1, 0, 2}
- A Δ B = {-3, -2, -1, 0, 2, 5, 7, 9}
- Ac = {-3, -2, -1, 0, 2, 4, 6, 8, 10}
- Bc = {4, 5, 6, 7, 8, 9, 10}
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
More information about each operation
Leave a Reply

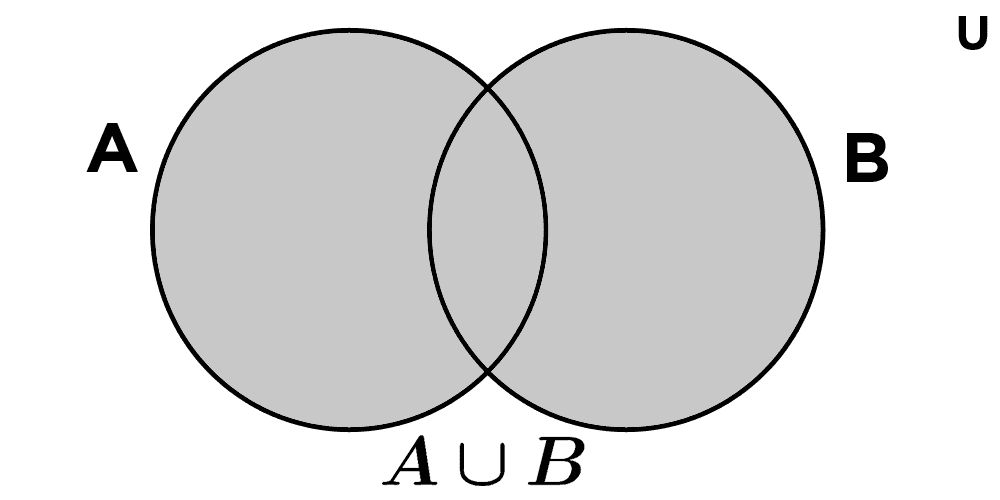
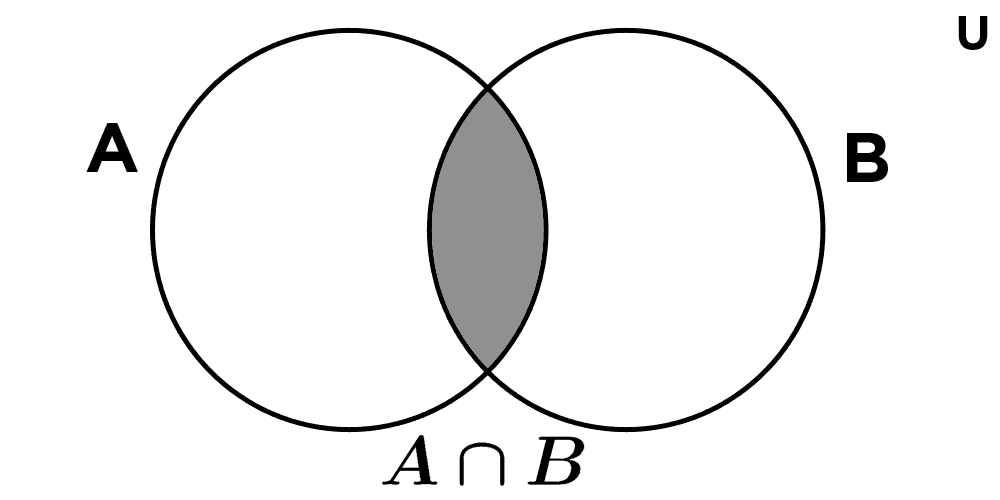
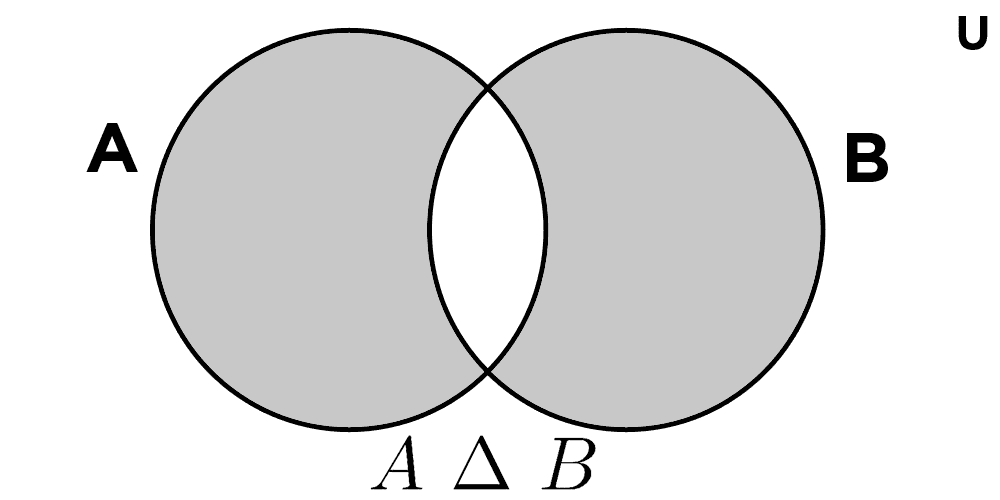



Related posts