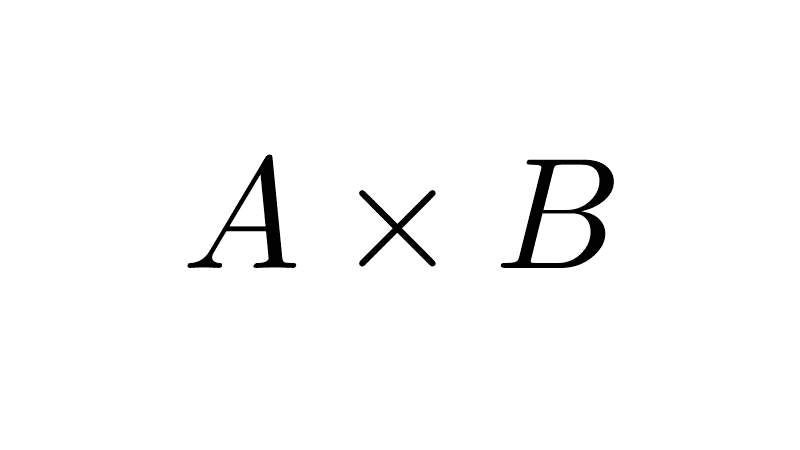
Equality of Sets
Two sets are equal if they have exactly the same elements, regardless of the order in which they are presented or if they are repeated. The equality relation is symbolized by "=". Thus, if A and B are two equal sets, it is written as A = B.
One way to determine if two sets are equal is to check if they are subsets of each other. This comes from the antisymmetric property of set inclusion:
A = B if and only if A ⊆ B and B ⊆ A
Two sets are not equal if one contains an element that the other does not. For inequality, the symbol "≠" is used. Therefore, if A and B are different, it is written as A ≠ B.
Unlike equivalence, where sets only need to have the same cardinality, to be equal, sets must have the same cardinality and also the same elements.
Table of Contents
Examples
- The set A = {1, 2, 3} is equal to the set B = {3, 1, 2} because both have the same elements, even though they are written in a different order, so A = B.
- The set C = {a, b, c, c, b} and D = {b, a, a, b, c} are equal, as both have the same elements, even if they appear in a different order or are repeated.
- The set E = {-1, 0, 1} is different from the set F = {1, 2, 4}, because the elements "-1" and "0" are in E but not in F, and in turn, "2" and "4" are in F but not in E. Therefore, E ≠ F.
- The set M = {-2, 2} is equal to the set N = { x | x2 = 4 }, because we can write N in roster form as N = {-2, 2}, and we conclude that M = N.
- The infinite set of positive integers Z+ = {1, 2, 3, 4,...} is equal to the set of natural numbers N = {1, 2, 3, 4,...} because both have the same elements, so Z+ = N.
- The set of real numbers R is different from the set of rational numbers Q, because there are real numbers that are not rational, but are irrational (like π, e, √2, etc.). Therefore, R ≠ Q.
Properties of Equality
The set equality relation satisfies the following properties.
- Reflexivity: Every set is equal to itself. That is, A = A for any set A.
- Symmetry: If a set is equal to another, then the second set is also equal to the first. That is, if A = B, then B = A.
- Transitivity: If a set is equal to another, and that one is equal to a third, then the first set is equal to the third. That is, if A = B and B = C, then A = C.
Practice Exercises
Exercise: If *A=\{-4; 9x+2y\}* is equal to the set *B=\{x+1; 27\},* determine the value of *x+y.*
Solution
Since sets A and B must be equal, all their elements must be equal. Now, since -4 cannot be equal to 27, it must be that *9x+2y=27.* At the same time, *x+1=-4.* That is, we must solve the system:
*\begin{cases} 9x+2y=27 \\ x+1=-4 \end{cases}*
We can easily solve for x: *x=-5* and substitute it into the first equation to solve for y:
*9\cdot (-5)+2y=27*
*-45+2y=27*
*2y=27+45*
*2y=72*
*y=36*
Therefore, the values *x=-5* and *y=36* make both sets equal. Their sum is *x+y=-5+36=31*
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

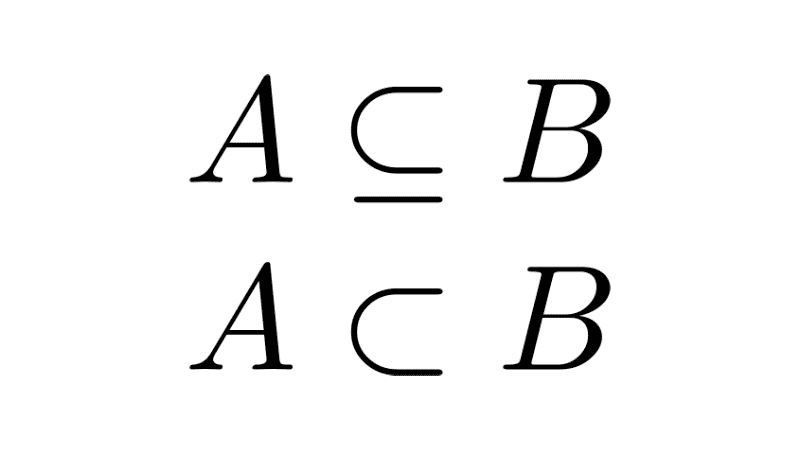

Related posts