Set Inclusion
Inclusion is a relation between two sets where all elements of the first set are also elements of the second. In other words, the first set is contained within the second. There are two types of inclusion: general (subset) and strict (proper subset).
Table of Contents
Inclusion
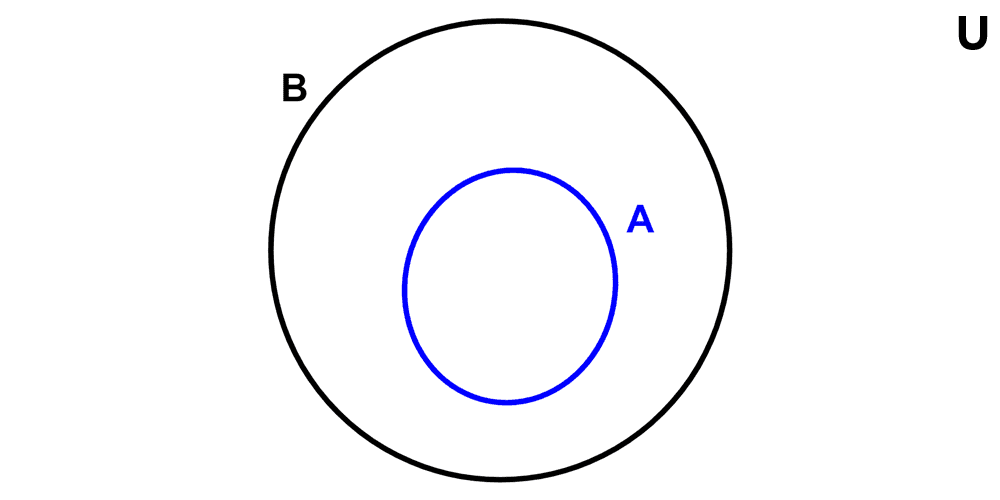
A set is a subset of another if the elements of the first are also elements of the second, and the two sets can be equal. This relationship is symbolized by ⊆:
A ⊆ B if and only if ∀x: (x ∈ A → x ∈ B)
If a set A is a subset of a set B, we say that A is a subset of B. Since this type of inclusion is the most commonly used, we will simply call it "inclusion"; when we want to refer to the other type, we will specify it accordingly.
To indicate that a set is not a subset of another, the crossed-out symbol ⊈ is used. Thus, A ⊈ B means that A is not a subset of B.
Examples
- The set A = {1, 2, 3} is a subset of the set B = {1, 2, 3, 4, 5} because the elements of A are also elements of B, so A ⊆ B.
- The set C = {a, b, c, d} is a subset of the set D = {1, 2, 3, a, b, c, d, e} because every element of C is also contained in D, so C ⊆ D.
- The set M = {-1, 0, 1} is not a subset of N = {1, 0} because M has elements that are not in N, so: M ⊈ N. However, we can note that N is a subset of M, so N ⊆ M.
- The set E = {1, 2} is a subset of F = {2, 1} because every element of E is also an element of F, so E ⊆ F. The reciprocal relationship is also true: F ⊆ E. This occurs because sets E and F are equal.
- The set of natural numbers N is a subset of the set of integers Z because every natural number is also an integer, so: N ⊆ Z. The reciprocal relationship is not true because there are integers that are not natural numbers (zero and the negative numbers), so Z ⊈ N.
Based on the examples, we can say that to prove a set is a subset of another, one must show that every element of the first is also an element of the second.
Properties of Inclusion
The subset relation satisfies the following properties:
1) Reflexivity: every set is a subset of itself, i.e., A ⊆ A.
2) Antisymmetry: if a set is a subset of another and the second is in turn a subset of the first, then both sets are equal. That is, if A ⊆ B and B ⊆ A, then A = B.
3) Transitivity: if a set is a subset of another, and the second is in turn a subset of a third, then the first set is also a subset of the third. That is, if A ⊆ B and B ⊆ C, then A ⊆ C.
4) The empty set is a subset of every set, including itself. That is, Ø ⊆ A, and also Ø ⊆ Ø. The proof of this property comes from the definition:
Ø ⊆ A if and only if ∀x: (x ∈ Ø → x ∈ A)
Since the proposition x ∈ Ø is false, because the empty set has no elements, the implication x ∈ Ø → x ∈ A is true because it has a false antecedent. Therefore, it follows that Ø ⊆ A.
Strict Inclusion
A set is a proper subset of another if the elements of the first are also elements of the second, but there are elements in the second set that are not in the first, meaning the sets cannot be equal. This relationship is symbolized by ⊂:
A ⊂ B if and only if ∀x: (x ∈ A → x ∈ B) and also A ≠ B
If a set A is a proper subset of a set B, we say that A is a proper subset of B. To indicate that a set is not a proper subset of another, the crossed-out symbol ⊄ is used. Thus, A ⊄ B means that A is not a proper subset of B.
Examples
- The set A = {1, 2, 3} is a proper subset of the set B = {1, 2, 3, 4, 5} because the elements of A are also elements of B, and there are also elements in B that are not in A ("4" and "5"). Therefore A ⊂ B.
- The set E = {1, 2} is not a proper subset of F = {2, 1} because, although every element of E is also an element of F, there are no elements in F that are not in E. In other words, set F is not larger than E, therefore, strict inclusion does not hold: E ⊄ F.
Every strict inclusion is also an inclusion, but not every inclusion is strict. A set may not be a proper subset of another, but it can still be a subset, as shown in the second example.
Notation
The following table summarizes the notation used for set inclusion.
| Symbol | Meaning |
|---|---|
| A ⊆ B | A is a subset of B |
| A ⊈ B | A is not a subset of B |
| A ⊂ B | A is a proper subset of B |
| A ⊄ B | A is not a proper subset of B |
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply



Related posts