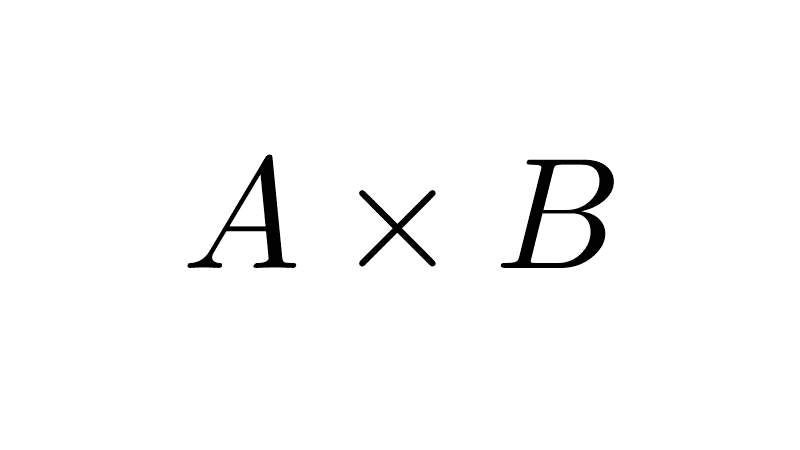
Cardinality of Sets
The cardinality of a set is the number of distinct elements it contains. The cardinality of a set A is denoted by |A| or Card(A).
For example, the set A = {a, b, c} has three elements, so its cardinality or size is that number: |A| = 3. The set B = {1, 2, 1} has two distinct elements, as "1" is listed twice, therefore |B| = 2.
If two sets have the same cardinality, they are said to be equivalent. For example, the sets C = {6, 9, 0} and D = {p, q, r} both have three distinct elements, therefore, they are equivalent and we can write |C| = |D|.
The cardinality of a set can be finite or infinite. For finite sets, like the previous cases, the cardinality is a non-negative integer that represents the number of distinct elements. For infinite sets, such as number sets, special notation is used.
Table of Contents
Cardinality of a finite set
To calculate the cardinality of a finite set, you simply count the number of unique elements it has.
Examples
- A = {1, 2, 3, 4, 4, 5} has five distinct elements, because the element "4" is repeated twice, so it is only counted once. Therefore, the cardinality of A is 5: |A| = 5.
- B = {-1, 5, 3, 7} has four unique elements, therefore, its cardinality is that number: |B| = 4.
- C = {green, blue, purple, blue} has three unique elements ("blue" is repeated twice and is only counted once), therefore, |C| = 3.
- D = {3, a, e, i, o, u, 3, o, 3} has six distinct elements, as "3" and "o" are repeated more than once and are only counted once. Thus, the cardinality is six: |D| = 6.
If the set is given in set-builder notation, you must first write it in roster form (if possible) to count its elements and thus determine its cardinality.
Examples
- J = {x | x is a letter in the word “sleepy”} is given in set-builder notation. Written in roster form, it is J = {s, l, e, e, p, y}, which has five distinct elements, because one of the letters is repeated twice, so: |J| = 5.
- The set E = { x | x+1 = 3 } is given in set-builder notation. Its equivalent in roster form is E = {2}, which has only one element, so its cardinality is one: |E| = 1. Sets with a cardinality of 1 are called singleton sets; in this example, E is a singleton set.
Exercise: determine the cardinality of the following sets.
A = {x | x is a vowel}
B = {x | x is a natural number, even, and less than or equal to 12}
C = {x | x-1=0}
D = {x, y, z, w, y}
Solutions:
|A| = 5
|B| = 6
|C| = 1
|D| = 4
Properties
The cardinality of a finite set has some properties that can be useful for calculating it.
1) Cardinality of the empty set
The cardinality of the empty set is zero, i.e., |Ø| = 0. This is evident because the empty set has no elements.
2) Cardinality of a subset
If a set A is a subset of another set B, then the cardinality of A is less than or equal to the cardinality of B. Symbolically, if A ⊆ B, then |A| ≤ |B|.
If A is a proper subset of B, then the cardinality of A is strictly less than the cardinality of B. In symbols, if A ⊂ B, then |A| < |B|.
3) Cardinality of the union
The cardinality of the union of two sets is the sum of their individual cardinalities minus the cardinality of their intersection. In symbols:
|A ∪ B| = |A| + |B| - |A ∩ B|
If sets A and B are disjoint (have no elements in common), then the cardinality of their union is simply the sum of their individual cardinalities, i.e.,
|A ∪ B| = |A| + |B|
4) Cardinality of the intersection
The cardinality of the intersection of two sets is the sum of their individual cardinalities minus the cardinality of their union. That is:
|A ∩ B| = |A| + |B| - |A ∪ B|
If A and B are disjoint sets, then the cardinality of their intersection is zero.
5) Cardinality of the difference
The cardinality of the difference between two sets A and B is equal to the cardinality of A minus the cardinality of the intersection of A and B, i.e.:
|A - B| = |A| - |A ∩ B|.
6) Cardinality of the complement
The cardinality of the complement of a set is equal to the cardinality of the universal set minus the cardinality of the set, i.e.,
|A’| = |U| - |A|
7) Cardinality of a Cartesian product
The cardinality of the Cartesian product of two sets A and B is the product of their respective cardinalities, i.e.:
|A × B| = |A| ⋅ |B|
8) Cardinality of a power set
The cardinality of a power set is equal to 2 raised to the power of the number of elements in the set. If a set has n elements, then the cardinality of its power set is 2n.
Cardinality of an infinite set
The cardinality of an infinite set is expressed with special symbols, as its elements cannot be counted. Mathematically, the cardinality of an infinite set is said to be a transfinite number.
For example, the cardinality of the set of natural numbers is symbolized as ℵ₀ (aleph-naught). The cardinality of the set of real numbers is symbolized as c (for continuum) or also as ℵ₁ (aleph-one).
It is intuitive to think that all infinite sets have the same number of elements, simply because they are infinite. However, this is not the case, and it can be proven that there are infinite sets that are "larger" than other infinite sets. In particular, the set of real numbers has more elements than the set of natural numbers: c > ℵ₀.
It can also be proven that infinite sets that seem to have more elements than others actually have the same number. Thus, the cardinalities of the set of integers and the set of rational numbers are equal to that of the natural numbers: |Q| = |Z| = |N| = ℵ₀. Also, any two intervals of real numbers have the same number of elements: c.
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

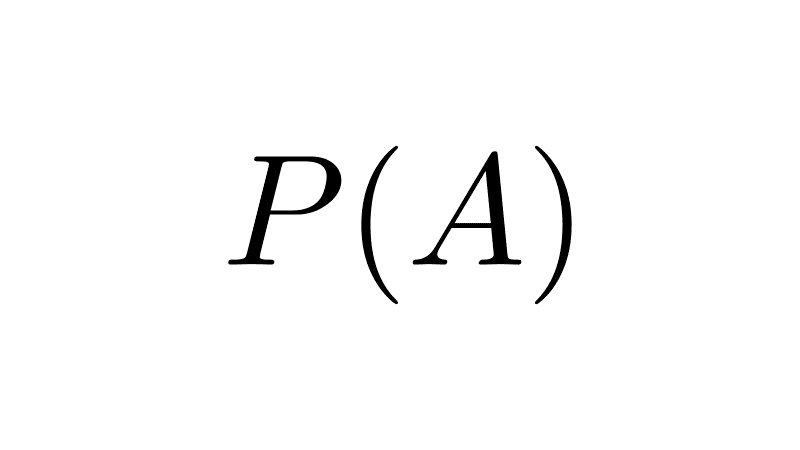
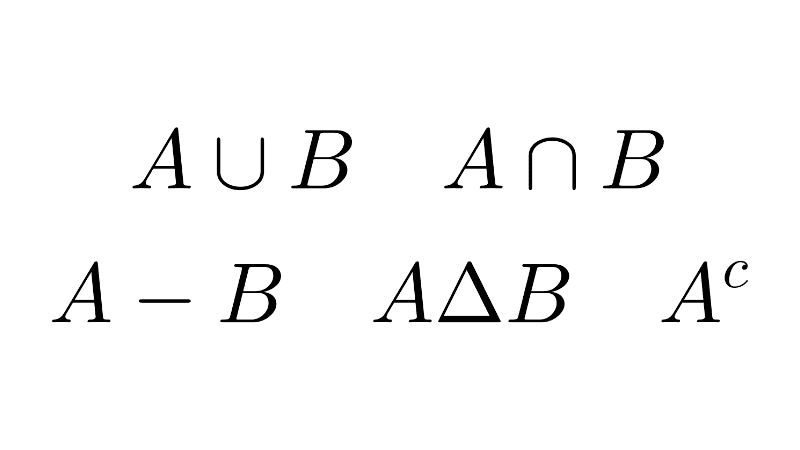
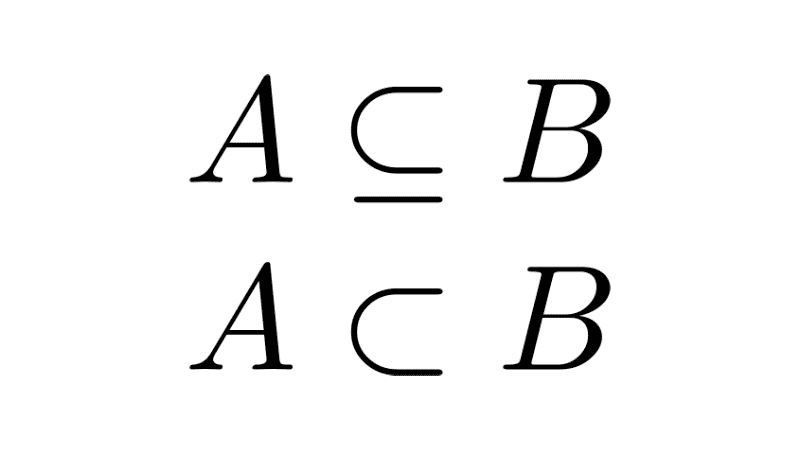
Related posts