What is a Set in Mathematics?
A set is a well-defined collection or grouping of objects, which are called elements. These objects can be concrete (people, animals, material objects, etc.) or abstract (numbers, ideas, concepts, relationships, etc.). The essential characteristic of a set is that it is clearly determined which elements belong to it and which do not.
A simple example of a well-defined collection is "the set of the days of the week": we know for certain that "Monday" belongs to the set, but "March" does not. In contrast, if we talk about "the set of beautiful songs," we cannot determine it precisely because it depends on each person's taste, so it does not constitute a valid mathematical set.
The notion of membership is key in set theory: an element can either belong or not belong to a set. To express this, specific symbols are used: if the element a belongs to the set A, it is written as a ∈ A; conversely, if it does not belong, it is written as a ∉ A.
In mathematics, sets are usually represented with uppercase letters (A, B, C, …), while elements are denoted with lowercase letters (a, b, c, …). It is important to note that, within the same set, the elements are unique (they are not repeated) and the order in which they are written does not alter the set. For example, the sets {1, 2, 3}, {1, 1, 2, 2, 3}, and {3, 1, 2} all represent exactly the same thing.
Although a set can in principle contain elements of any nature, even heterogeneous ones (like a number, a color, and an animal in the same set), in mathematics they are primarily used to organize and classify objects that share common properties. This allows for working with them in a structured way, establishing relationships between different collections, and performing operations on them.
Table of Contents
How Sets Are Represented
Expressing the elements that make up a set is known as defining the set. In mathematics, there are two main ways to do this in written form: in roster form, by listing each element, or using set-builder notation, by indicating the characteristic that the elements share. In addition to these written forms, sets can also be represented visually using Venn diagrams, which allow for the graphical illustration of the relationship between different sets.
Representation in Roster Form
This consists of explicitly writing all the elements that make up the set, separated by commas and enclosed in braces { }.
An important aspect we mentioned earlier is that the order of the elements does not matter and that elements are not repeated. For example, the sets {a, b, c}, {c, a, b}, and {a, b, b, c} all represent exactly the same thing.
Examples
- A = {a, b, c} is the set of the first three letters of the alphabet.
- B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} is the set of the first ten natural numbers.
- C = {-1, 1} is the set consisting of the numbers -1 and 1.
- D = {w, o, r, l, d} is the set of letters that form the word "world".
- E = {spring, summer, fall, winter} is the set of the seasons of the year.
Representation in roster form is clear and simple, but it is only practical when the set has a finite and small number of elements.
Representation Using Set-Builder Notation
Instead of listing the elements one by one, a common property or condition that all of them satisfy is described. The following notation is used for this purpose:
{ x | x satisfies a property }
This is read as "the set of all x such that x satisfies a certain property."
Examples
- P = { x | x is an even integer } is the set of all even integers.
- R = { x | x is a real number } is the set of all real numbers.
- { x | x is a real number and x ≥ 6 } is the set of all real numbers greater than or equal to 6.
- Q = { x | x is the square of a natural number } is the set of all perfect squares.
- V = { x | x is a vowel in the English alphabet } is the set of vowels.
The advantage of this form is that it allows for describing infinite or very large sets that could not be listed in roster form.
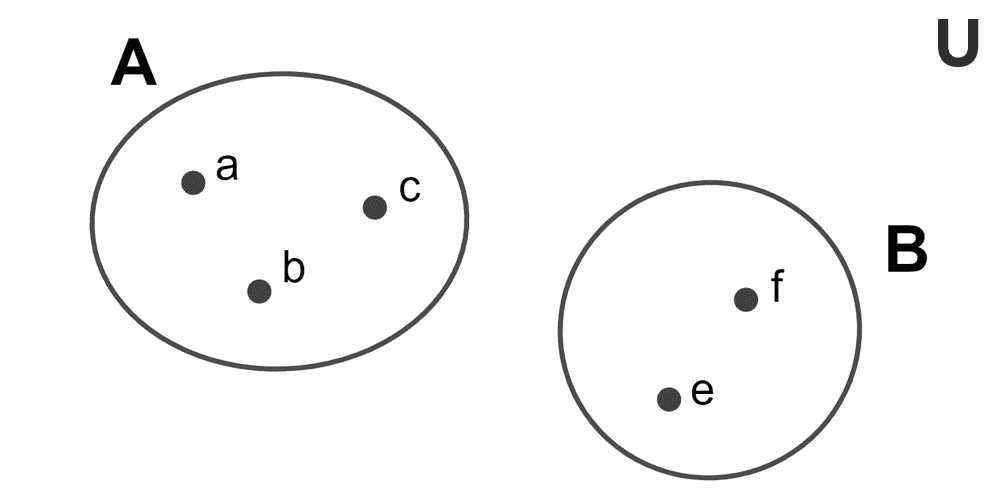
Representation Using Venn Diagrams
Venn diagrams are graphical representations that allow for the visualization of sets and their relationships. A rectangle is drawn for the universal set (all possible elements in the context), and within it, circles or ovals are used to represent particular sets.
For example: let the sets be A = {a, b, c} and B = {e, f}. In the diagram, they are represented as two distinct circles within the universal rectangle, with no intersection between them.
Types of Sets
There are different types of sets, some of which are:
- Finite set: a set that has a limited number of elements, such that we can count them all. For example, the set of the months of the year is finite because it contains twelve elements.
- Infinite set: a set that has no limit to its number of elements, and therefore, we cannot count them in their entirety. An example is the set of real numbers, which extends indefinitely towards both positive and negative values.
- Empty set (∅): a set that contains no elements. It is represented by the symbol ∅ or by empty braces {}. An example is the set of odd numbers that are divisible by 2, as no such number exists that satisfies this condition.
- Universal set (U): the set that contains all the elements relevant within a specific context and serves as a frame of reference for defining other sets. For example, if we are working with vowels, the universal set could be the entire alphabet.
Relationships Between Elements and Sets
So far, we have discussed the membership relation, which connects an element to a set. However, sets can also be related to each other, and one of the most important ways is through inclusion. Below, we will look at both relationships in more detail.
- Membership relation: an element belongs to a set if it is part of it, which is indicated by the symbol ∈. For example, if V = {a, e, i, o, u}, then a ∈ V because the letter 'a' is in V, whereas b ∉ V because 'b' is not part of the set of vowels.
- Inclusion relation: a set A is said to be a subset of B, written A ⊆ B, when all elements of A also belong to B. Thus, if A = {1, 2} and B = {1, 2, 3, 4}, then A ⊆ B because every element of A is found in B. When A is included in B but also A ≠ B, it is called a proper subset, symbolized as A ⊂ B.
Operations on Sets
Sets can be combined through various operations, which allows for constructing new collections from existing ones and analyzing how they interact. The most common ones are:
- Union (∪): the union of two sets A and B is the set of all elements that are in A, in B, or in both. It is defined as A ∪ B = {x | x ∈ A or x ∈ B}. For example, {1, 2} ∪ {2, 3} = {1, 2, 3}.
- Intersection (∩): the intersection of A and B is formed by the elements that belong to both sets simultaneously. It is written as A ∩ B = {x | x ∈ A and x ∈ B}. For example, {1, 2} ∩ {2, 3} = {2}.
- Difference (–): the difference A – B is the set of elements that belong to A but not to B. It is expressed as A – B = {x | x ∈ A and x ∉ B}. For example, {1, 2} – {2, 3} = {1}.
- Complement: the complement of a set A, with respect to a universal set U, is defined as Ac = {x | x ∈ U and x ∉ A}. Thus, if U = {1, 2, 3, 4, 5} and A = {2, 4}, then Ac = {1, 3, 5}.
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

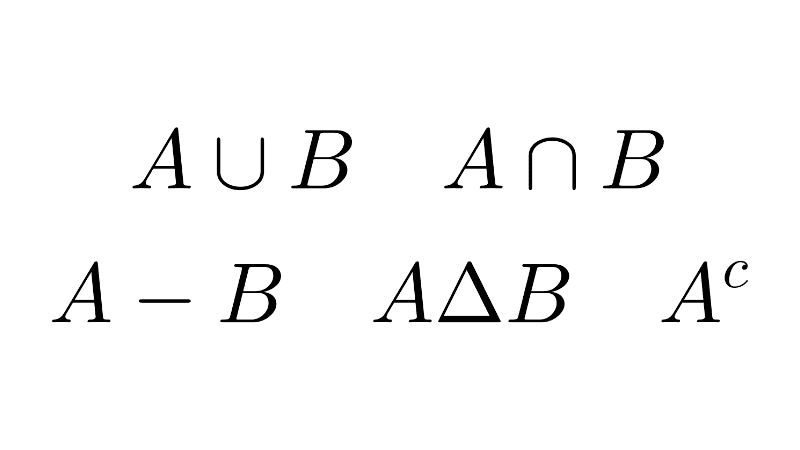
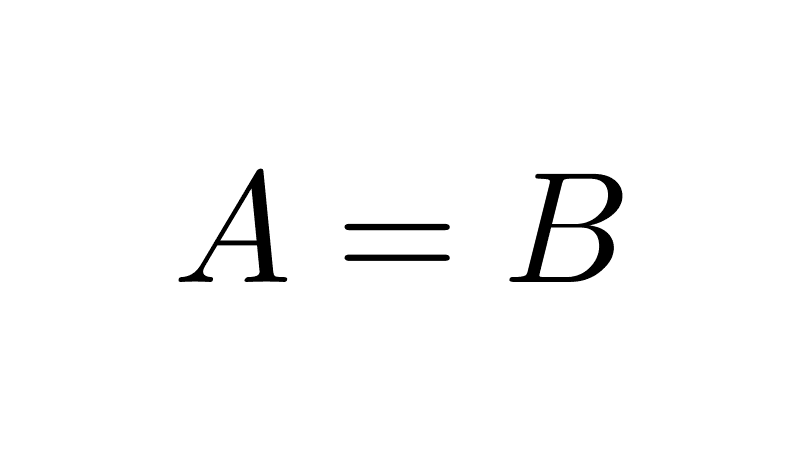
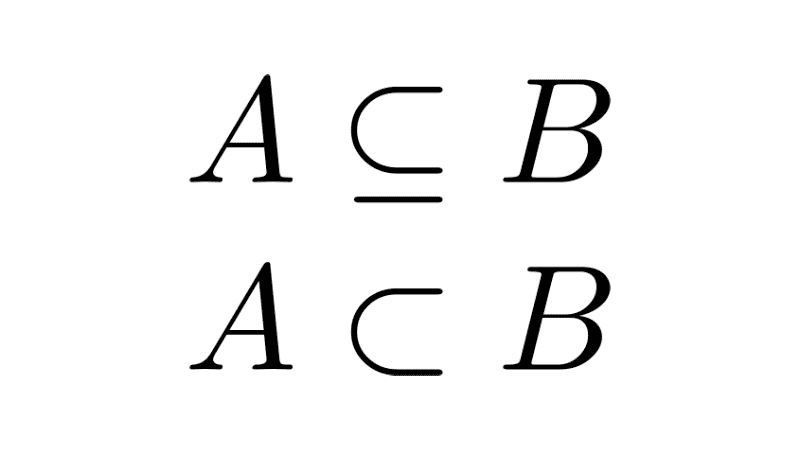
Related posts