Types of Mathematical Sets
There are different types of sets in set theory. We have compiled several of them in the following table:
| Name | Description | Examples |
|---|---|---|
| Finite set | A finite set is one that has a limited number of elements. | A = {a, e, i, o, u} B = {x | x is a vowel} |
| Infinite set | An infinite set is one that has an unlimited number of elements. | N = {1, 2, 3, ...} (the set of natural numbers). P = {x | x is an even integer} (the set of even integers). |
| Empty set | The empty set, represented by { } or Ø, is a set that has no elements. | The set of planets orbiting the moon is Ø. The set of solutions to the equation x ⋅ 0 = 4 is empty: Ø = {x | x ⋅ 0 = 4} |
| Singleton set | A singleton set is a set that contains only one element. | A = {z} is a singleton set. The set of solutions to the equation 2 ⋅ x = 4 is a singleton set: {x | 2⋅x = 4} = {2} |
| Universal set | The universal set is the set that contains all the relevant elements for a given context. | When working with natural numbers, the universal set is the set of all natural numbers: N. When working with triangles, the universal set is the set of all triangles. |
| Complement of a set | The complement of a set A, denoted as A', is the set of all elements that are in the universal set but are not in A. | The complement of the set of odd integers is the set of even integers. The complement of the set of equilateral triangles is the set of triangles that are not equilateral (isosceles and scalene). |
| Power set | The power set of a set is the set containing all possible subsets of that original set. | The power set of A = {a, b} is P(A) = {Ø, {a}, {b}, {a, b}}. The power set of Ø is P(Ø) = {Ø}. |
| Number sets | Number sets are sets that contain numbers with certain common characteristics. | Natural numbers (N) Integers (Z) Rational numbers (Q) Irrational numbers (I) Real numbers (R) Complex numbers (C) |
| Subset | A set A is a subset of another set B if all elements of A are also in B. | The set A = {dog, cat} is a subset of B = {dog, cat, bird}. The set of natural numbers N is a subset of the set of integers Z. |
| Proper subset | A set A is a proper subset of B if all elements of A are also in B, but A ≠ B. | A = {1, 2} is a proper subset of B = {1, 2, 3}. The set of even integers is a proper subset of the set of integers. |
| Equivalent sets | Two sets are equipotent or equivalent if they have the same number of elements (the same cardinality). | The sets A = {a, b, c} and B = {7, 8, 9} are equipotent because they have the same number of elements. The set of letters in the word "math" and the set of integers from 1 to 4 are equivalent because both have four elements. |
| Equal sets | Two sets are equal if they have the same elements, regardless of order. | The set A = {a, b, c} is equal to B = {c, b, a}. The set {1, -1} is equal to the set {x | x2 = 1} |
| Disjoint sets | Two sets are disjoint if they share no elements in common. | The sets A = {1, 2} and B = {3, 4} are disjoint because they share no elements. The set of positive real numbers and the set of negative real numbers are disjoint, because no number can be both positive and negative at the same time. |
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

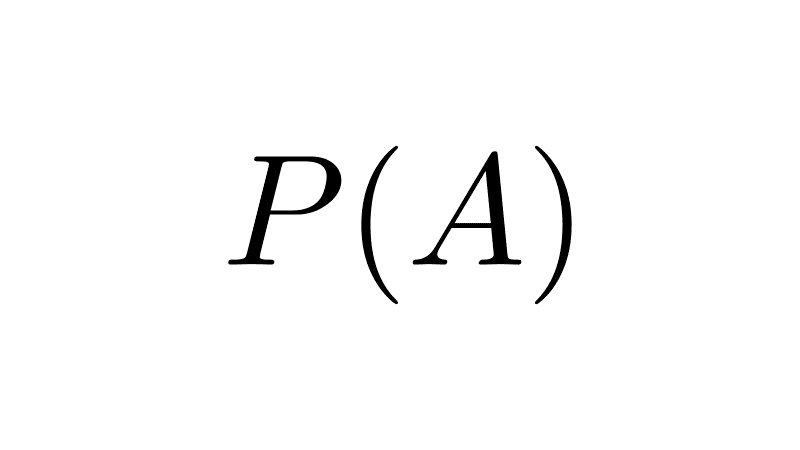
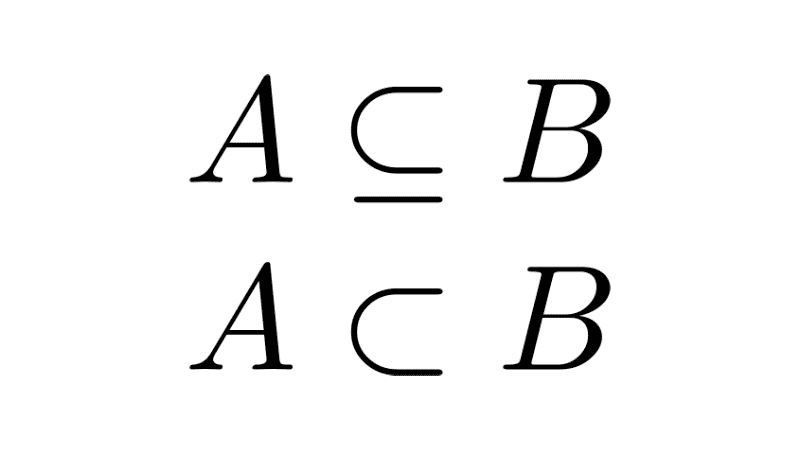
Related posts