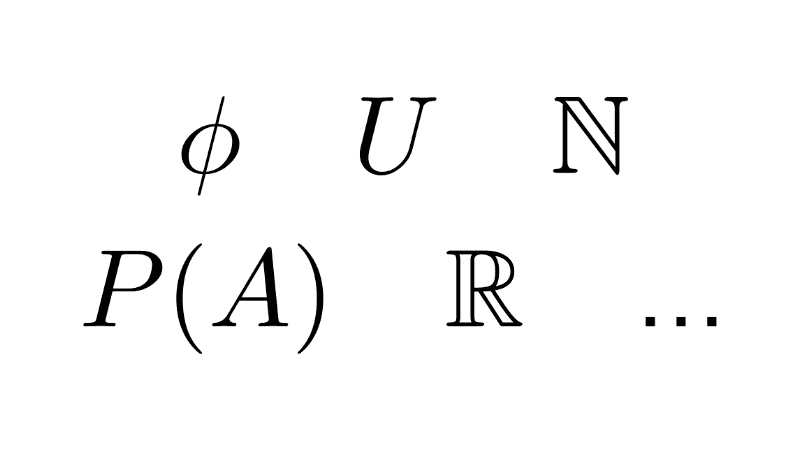
Set Theory
Set theory is a branch of mathematics that studies the properties and relationships of sets, which are well-defined collections of objects. These sets can contain numbers, letters, functions, or other sets, depending on the context.
Set theory was developed in the late 19th century by mathematicians such as Georg Cantor and Richard Dedekind. It provides a formal framework for constructing other mathematical structures and is used extensively in virtually all fields of mathematics, as well as in logic and computer science.
Table of Contents
Basic Concepts
The fundamental concepts of set theory are the set, element, and membership. Based on these, cardinality, inclusion relations, set equality, and other operations are defined.
Set
A set is a collection of well-defined and distinct objects. These objects can be concrete (numbers, letters) or abstract (ideas, concepts).
Sets are denoted by uppercase letters A, B, C, etc. The elements are written inside curly braces {}, separated by commas.
Examples:
- A = {1, 2, 3}
- B = {a, b, c}
- C = {red, green, blue}
Element
An element is an object that is part of a set. It can be anything, such as a number, a letter, a person, an animal, a physical object, or even an abstract concept.
Two identical elements in the same set are considered as one. Also, the order in which the elements are written does not matter; the set remains the same.
Examples:
- The set A = {1, 2, 3} has three elements: the number 1, the number 2, and the number 3.
- The set B = {a, b, c} has three elements: the letter "a", the letter "b", and the letter "c".
- The set C = {red, green, blue} has three elements: the color red, the color green, and the color blue.
Membership
Membership is the relationship an element has with a set, indicating whether it is part of the set or not. To indicate that an element belongs to a set, the symbol ∈ is used; otherwise, the symbol ∉ is used.
Examples:
- 1 ∈ A (the number 1 belongs to set A)
- c ∈ B (the letter "c" belongs to set B)
- red ∈ C (the color red belongs to set C)
- 4 ∉ A (the number 4 does not belong to set A)
- d ∉ B (the letter "d" does not belong to set B)
Cardinality
The cardinality of a set is a measure that indicates how many elements the set has. In other words, it is the number of distinct elements contained in the set. The cardinality of a set A is symbolized by Card(A) or |A|.
Examples:
- The cardinality of the set B = {a, b, c} is |B|=3, because it has three elements.
- The cardinality of the set D = {1, 2, e, f, g} is |D|=5, because it has five elements.
The cardinality of a set can be finite or infinite. For finite sets, like the examples above, the cardinality is simply the number of elements in the set. For infinite sets, such as the set of all natural numbers (1, 2, 3, 4, ...), the cardinality is infinite and is expressed using special symbols, like ℵ₀ (aleph-null).
Equality of Sets
Two sets are equal if they have exactly the same elements, regardless of the order in which they are written.
Examples:
- A = {1, 2, 3} and E = {3, 1, 2} are equal sets.
- C = {red, green, blue} and F = {red, blue, green} are equal sets.
- B = {a, b, c} and G={a, b, c, d} are not equal sets, because they do not have the same elements.
Set Inclusion
If every element of a set A is also an element of a set B, then A is said to be included in B, or that A is a subset of B. Symbolically, this is written as A⊆B.
A ⊆ B if and only if ∀x: (x ∈ A → x ∈ B)
If at least one element of A is not in B, A is said to be not a subset of B, written as A⊈B. If every element of A is in B, but B has at least one element that is not in A, then A is a proper subset of B, symbolized as A⊂B.
Examples:
- A = {1, 2} is a subset of B = {1, 2, 3, 4, 5}, because every element of A is also an element of B: A⊆B. It is also true that A⊂B, because B has elements that are not in A.
- C = {red, green} is a subset of D = {red, green, blue}, so C ⊆ D.
Set Operations
There are several operations that can be performed between two or more sets, also known as set algebra. They are:
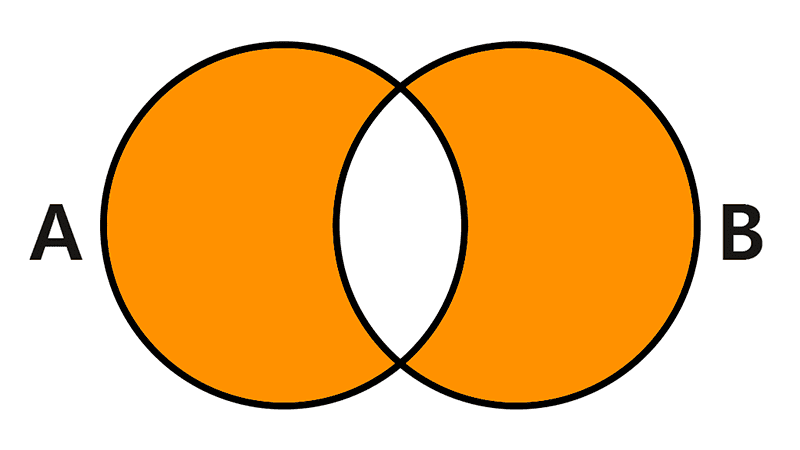
- Union: The union of two sets A and B is the set containing all elements that are in A, or in B, or in both. It is denoted by A ∪ B.
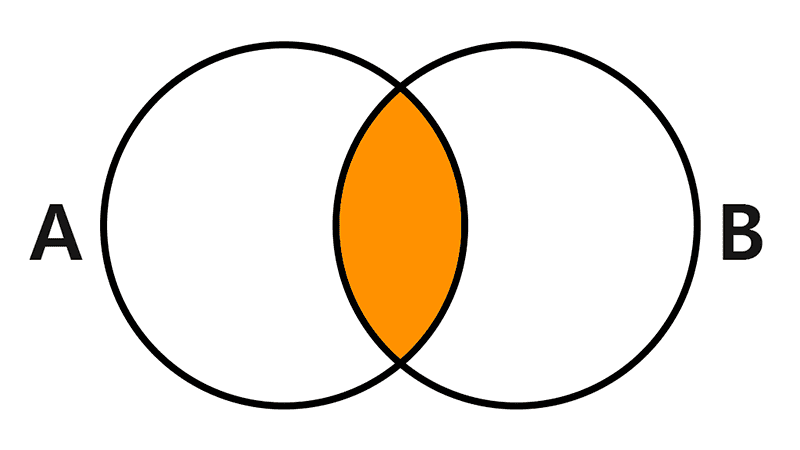
- Intersection: The intersection of two sets A and B is the set containing all elements that are in both A and B. It is denoted by A ∩ B.
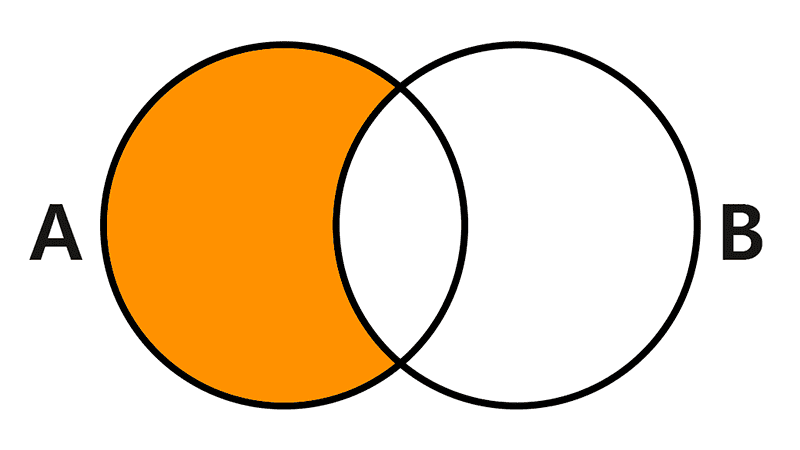
- Difference: The difference of two sets A and B is the set containing all elements that are in A but not in B. It is denoted by A-B.
- Symmetric Difference: The symmetric difference between two sets A and B is the set of elements which are in either of the sets, but not in their intersection. It is denoted by A Δ B.
- Complementation: The complement of a set A is the set A' composed of all the elements of the universal set U that are not in A. The universal set is the set that contains all the elements relevant to the particular context of study.
Types of Sets
In set theory, there are several types of sets, some of which are:
- Finite set: A set that has a finite number of elements.
- Infinite set: A set that has an infinite number of elements.
- Empty set: The set that has no elements. It is denoted by Ø.
- Singleton set: A set that contains exactly one element.
- Universal set: A set that contains all the relevant elements in a given context. It is typically denoted as U.
- Power set: The power set of A, denoted as P(A), is the set containing all possible subsets of A, including the empty set and A itself.
Some special sets that can be highlighted are the number sets, which contain numbers with certain common properties: natural (N), integers (Z), rational (Q), irrational (I), real (R), complex (C).
Venn Diagrams
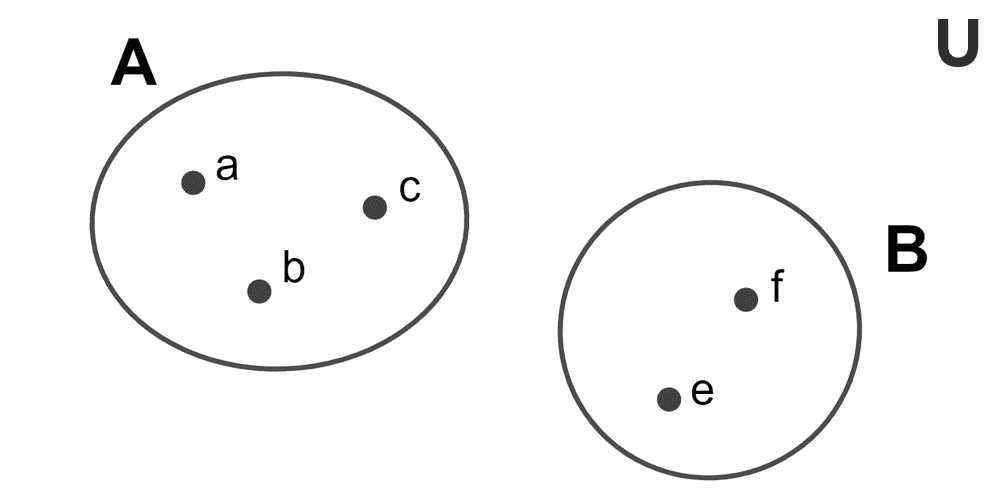
Sets are often represented graphically using what are called Venn diagrams. These diagrams are closed planar figures; typically, the universal set is represented by the interior of a rectangle, and other sets by circles within the rectangle. The corresponding elements are placed inside these figures.
For example, for the sets A = {a, b, c} and B = {e, f}, the Venn diagram is as follows:
Notation
The following tables show all the necessary notation for working with set theory, along with their meanings.
Basic Set Notation and Operations
| Symbol | Meaning |
|---|---|
| { } | Set: a collection of well-defined objects. |
| a ∈ A | The element a belongs to set A. |
| b ∉ A | The element b does not belong to set A. |
| |A| | Cardinality of set A. |
| A = B | Sets A and B are equal. |
| A ⊆ B | A is a subset of B. |
| A ⊂ B | A is a proper subset of B. |
| A ⊈ B | A is not a subset of B. |
| A ⊄ B | A is not a proper subset of B. |
| A ∪ B | Union of sets A and B. |
| A ∩ B | Intersection of sets A and B. |
| A - B | Difference between sets A and B. |
| A Δ B | Symmetric difference between sets A and B. |
| U | Universal set |
| A' | Complement of set A. |
| Ø | Empty set. |
| P(A) | Power set of set A. |
| A x B | Cartesian product A by B. |
Predicate Logic Notation for Sets
| Symbol | Meaning |
|---|---|
| | | such that |
| : | such that |
| ∀ | Universal quantifier: "for all" |
| ∃ | Existential quantifier: "there exists" |
| ∃! | Unique existential quantifier: "there exists only one" |
| ∴ | Therefore |
Number Sets
| Symbol | Set |
|---|---|
| N | Natural numbers |
| Z | Integers |
| Q | Rational numbers |
| I | Irrational numbers |
| R | Real numbers |
| C | Complex numbers |
Content About Sets
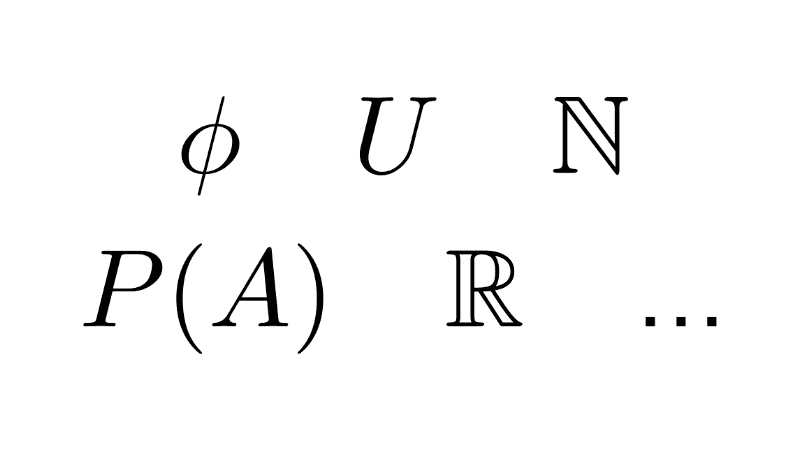
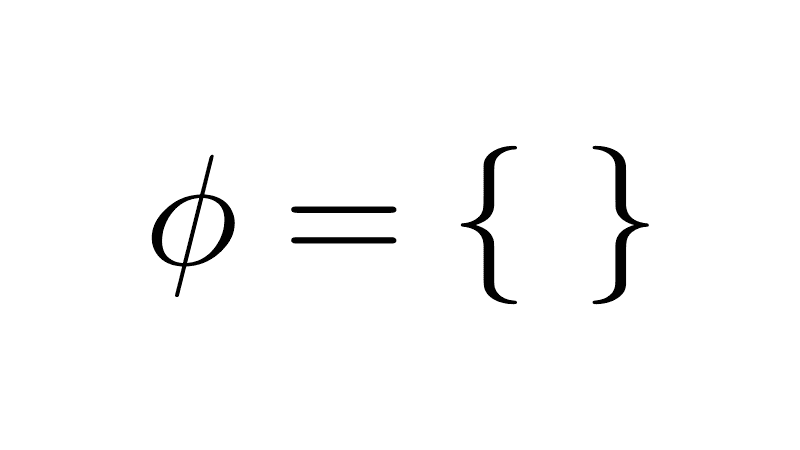
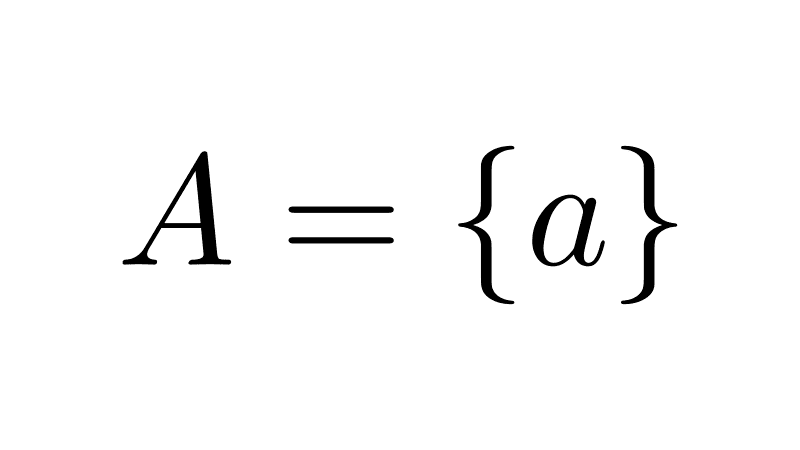
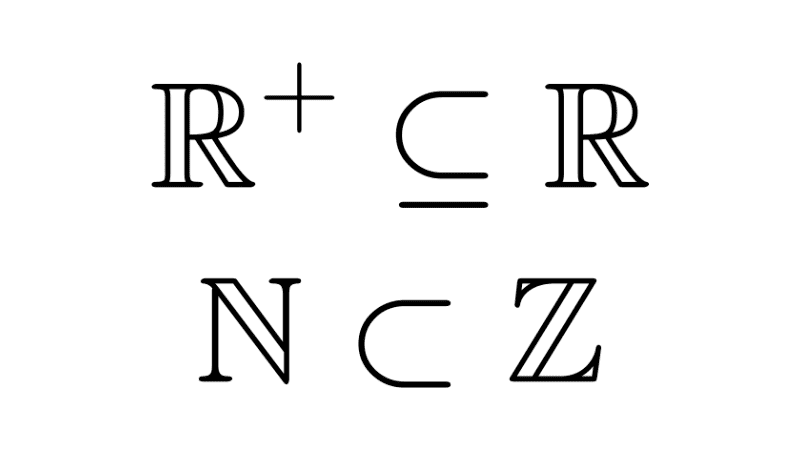
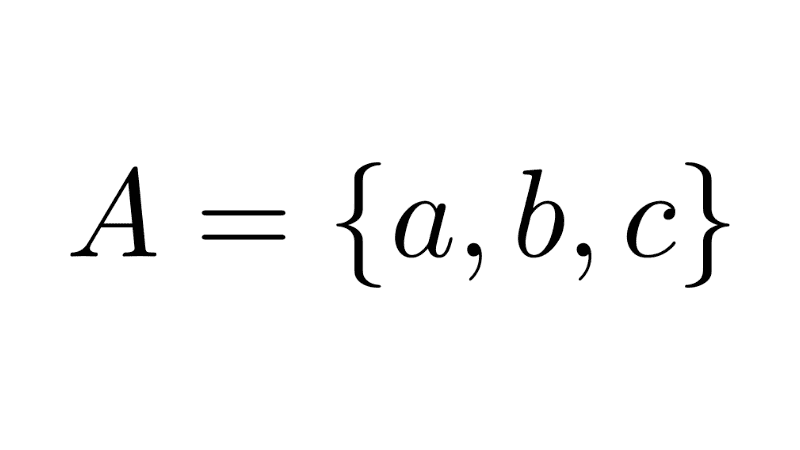

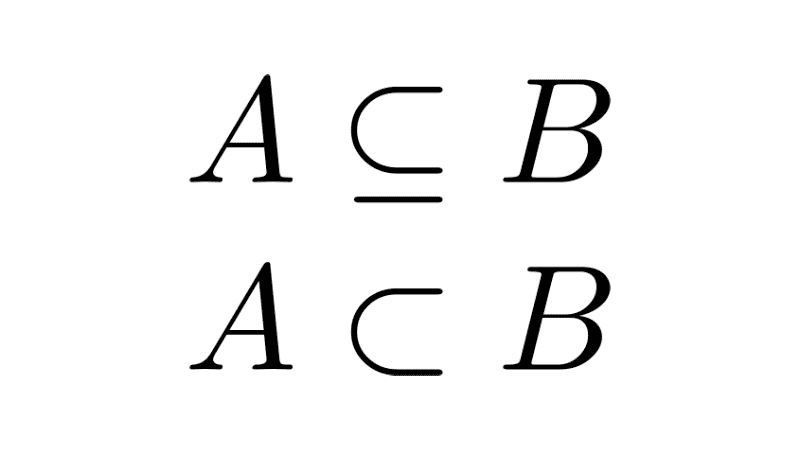
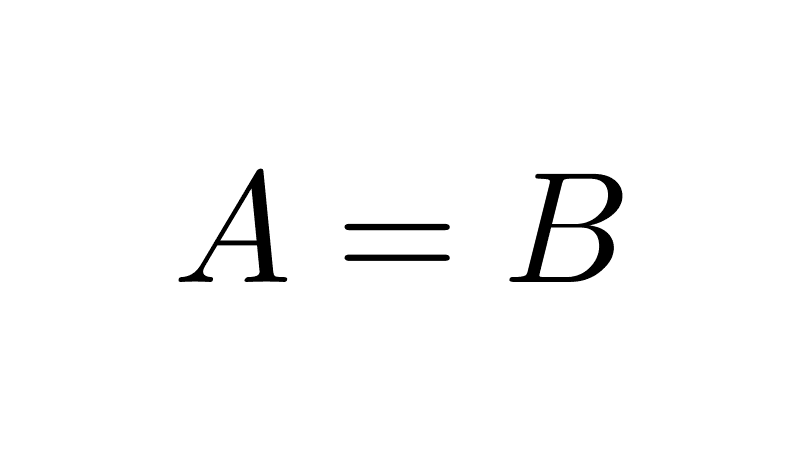
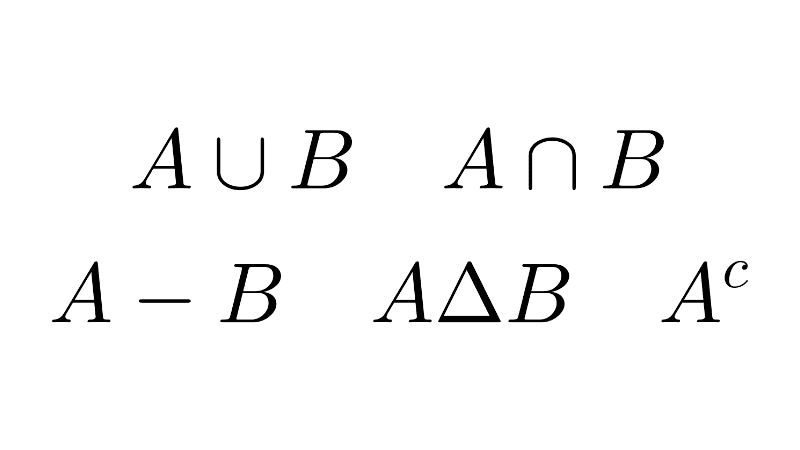
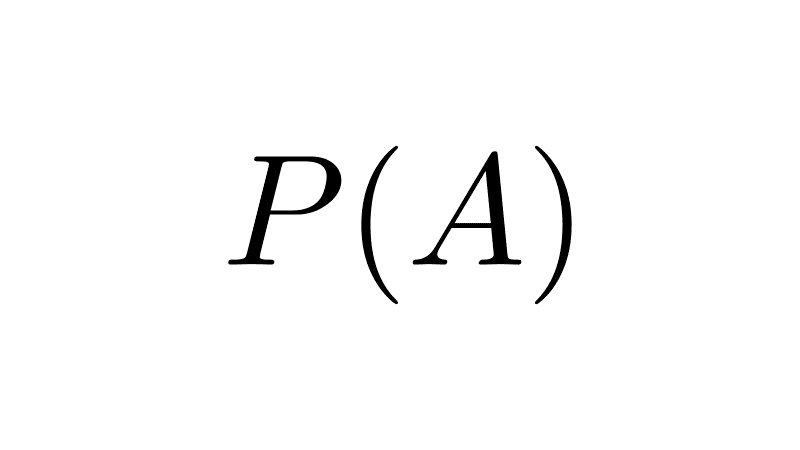
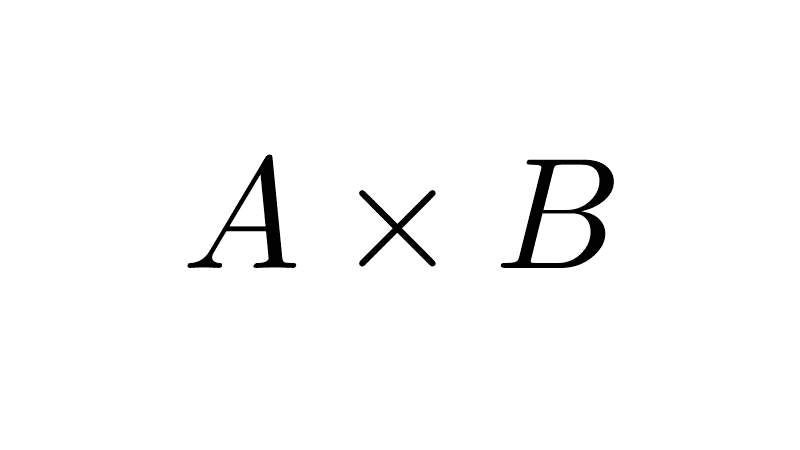



Leave a Reply