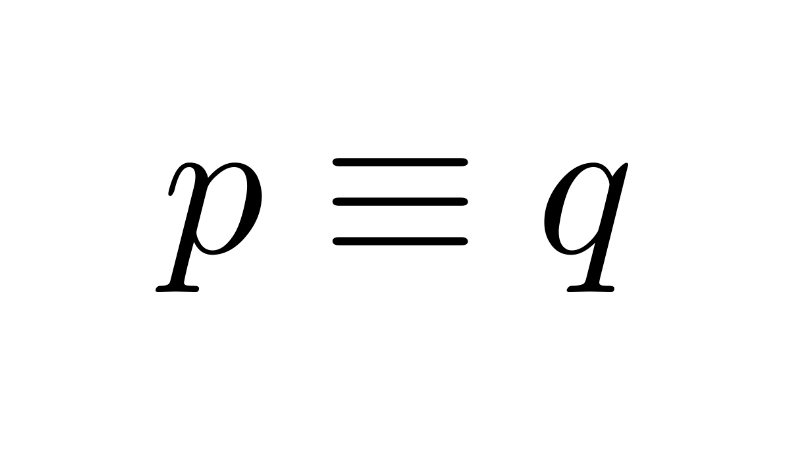
Propositional Function

A propositional function is an expression containing one or more variables that becomes a logical proposition (i.e., a statement that can be either true or false) when specific values are assigned to its variables or the expression is quantified.

Statements of this type are also called propositional schemas, open propositional formulas, or open propositions. They are symbolized using capital letters P, Q, R, S, etc., with the variables in parentheses. For example:

• P(x): x > 3
• Q(y): y + 5 = 8
• R(x, y): x + 5 = y + 3
• S(x): “x is an even number”
• T(z): “z has black hair”

These statements are not propositions because it cannot be determined whether they are true or false, as the values of the variables x, y, and z are unknown. If, for example, we take the expression "P(x): x > 3" and assign x the value 5, the statement becomes "P(5): 5 > 3," which is a proposition and, in this case, is true. If we were to set x = 0, it would become "P(0): 0 > 3," which is a false proposition.

How to Convert a Propositional Function into a Proposition

There are two ways to convert a propositional function into a proposition: by substitution and by quantification.

Substitution

Substitution consists of assigning a specific value to the variable or variables of the propositional function. By doing so, the ambiguity is removed, and a concrete proposition that can be either true or false is obtained.

The set of all possible terms that can be used in the substitution is called the universe of discourse, U. This universe is the set of all values that the variables can take.

Example

Let the propositional function be: P(x): x > 0 with the universe of discourse: U = {1, 2, 3, -1, -2, -3}. By substituting x = 3, we get the proposition 3 > 0, which is true. By substituting x = -2, we get -2 > 0, which is a false proposition.

The truth set is the set of all elements from the universe of discourse that make the proposition true when substituted for the variable. In the previous example, the truth set is {1, 2, 3}, as the other values will make the proposition false.

Quantification

Quantification is a different process where, instead of assigning a specific value to the variables, a symbol called a quantifier is placed before the expression. The quantifier indicates how the propositional function will be evaluated with respect to all or some elements of the domain. The most common quantifiers are the universal and existential quantifiers.

Some examples of quantification in everyday language are: "all Argentinians are Latin American," "some students passed the exam."

1) Universal quantifier (∀): means "for all," "for any," or "for each." Symbolically, it is written as ∀x: P(x), which is read as "for all x, P(x) holds true." The quantified proposition is true when all values in the domain (universe of discourse) satisfy the property.

Examples

• ∀ x ∈ N: x + 1 > x (for every natural number, adding 1 to it results in a larger number).
• ∀ x ∈ R: x² ≥ 0 (the square of any real number is greater than or equal to zero).
• ∀ x ∈ Z: x + (-x) = 0 (the sum of an integer and its opposite is zero).
• ∀ x ∈ Q: 2x ∈ Q (twice a rational number is still a rational number).

2) Existential quantifier (∃): which means "there exists at least one." Symbolically, it is written as ∃x / P(x), which is read as "there exists an x such that P(x)." The quantified proposition is true when at least one element in the domain satisfies the property.

Examples

• ∃x ∈ Z / x² = 4 (there exists an integer whose square is 4).
• ∃x ∈ Q / x² = 2 (there exists a rational number whose square is 2; this proposition is false).
• ∃x ∈ R / x < 0 (there exists at least one real number that is negative).
• ∃x ∈ N / “x is a multiple of 10” (there exists a natural number that is a multiple of 10).

Quantifiers, both universal and existential, apply to the closest propositional function unless modified by parentheses. For example: ∀x: P(x) ∨ Q(x) is interpreted as [∀x: P(x)] ∨ Q(x). If we wanted the quantifier to apply to both functions, we must write ∀x: [ P(x) ∨ Q(x) ].

Negation of Quantifiers

In predicate logic, when a proposition containing a quantifier is negated, the quantifier changes type, and the inner proposition is also negated. This is known as the quantifier negation rule and is fundamental for transforming or proving logical equivalences.

The rules are as follows:

1) The negation of a universal quantifier becomes an existential quantifier: 

¬(∀x: P(x)) ≡ ∃x / ¬P(x)

That is, "it is not true that all x satisfy P(x)" is equivalent to "there exists at least one x that does not satisfy P(x)."

2) The negation of an existential quantifier becomes a universal quantifier:

¬(∃x / P(x)) ≡ ∀x: ¬P(x)

That is, "there is no x that satisfies P(x)" is equivalent to "all x do not satisfy P(x)."

Examples

1) Let P(x): x > 0, then:

¬(∀x: x > 0) ≡ ∃x / x ≤ 0

That is, "not all numbers are positive" is equivalent to "there exists at least one number that is not positive."

2) Let Q(x): x² < 0, then:

¬(∃x ∈ R / x² < 0) ≡ ∀x ∈ R : x² ≥ 0

That is, "there is no real number whose square is negative" is equivalent to "all real numbers squared are non-negative."

Bibliography

• Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
• Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
• Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
• Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
• Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
• Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
• Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.