Logical Conjunction
Conjunction is a logical connective that connects two propositions and is true only if both propositions are true. If at least one of the two propositions is false, the conjunction is false. It is represented by the symbol ∧, which is usually read as "and".
Some examples of conjunction are:
- If p is "it is cold" and q is "it is snowing," their conjunction is p ∧ q: "it is cold and it is snowing."
- If p is "4 is an even number" and q is "5 is an odd number," the conjunction is p ∧ q: "4 is an even number and 5 is an odd number."
- If r is "John studies hard" and s is "John is a good writer," the compound proposition r ∧ s is "John studies hard and is a good writer."
The symbols "&" or "and" are also sometimes used, mainly in computer science. The conjunction symbol "∧" should not be confused with the disjunction symbol "∨". While conjunction is a "peak" pointing upwards, disjunction is one pointing downwards.
Table of Contents
Truth Table
As mentioned before, in propositional logic, conjunction is true when the simple propositions that form it are true, and it is false otherwise, whether one of them is false or both are. The truth table that represents this is:
| p | q | p ∧ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
For example, the proposition "it is cold and it is snowing" is true only when it is true that it is cold and it is snowing. The statement "4 is an even number and 5 is an odd number" is true because it is true that 4 is even and 5 is odd. The proposition "a triangle has three sides and a square has eight sides" is false, because while it is true that a triangle has three sides, it is not true that a square has eight.
Properties of Conjunction
1) Commutative Law: the order of the propositions does not affect the meaning.
p ∧ q ≡ q ∧ p
2) Associative Law: the grouping of the propositions does not affect the meaning.
p ∧ (q ∧ r) ≡ (p ∧ q) ∧ r
3) Identity element: the identity element for conjunction is the true value (T).
p ∧ T ≡ p
4) Absorbing element: the absorbing element for conjunction is the false value (F).
p ∧ F ≡ F
5) Distributive Law over disjunction: conjunction distributes over disjunction and vice versa.
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
6) Negation of conjunction (De Morgan's Law): the negation of a conjunction can be expressed in terms of the disjunction of the negations.
¬(p ∧ q) ≡ ¬p ∨ ¬q
7) Idempotence: the conjunction of a proposition with itself is equivalent to the original proposition.
p ∧ p ≡ p
8) Conjunction elimination: this is a valid rule of inference that allows one to assert one of the components of a conjunction from the truth of the entire conjunction. Symbolically:
p ∧ q → p
p ∧ q → q
9) The conjunction of a proposition and its negation is a contradiction, meaning p ∧ ¬p is always false.
Conjunction in Set Theory
In set theory, logical conjunction is used to define the intersection of sets, which is an operation that combines two sets to form a new set containing only the elements that belong to both original sets.
A ∩ B = {x | x ∈ A ∧ x ∈ B}
Examples:
- If A = {1, 2, 3} and B = {2, 3, 4}, then A ∩ B = {2, 3}.
- Given A = {a, b, c, d} and B = {d, e, f, g}, then A ∩ B = {d}.
- If A = {red, blue, green} and B = {yellow, orange}, then A ∩ B = ∅ (empty set), since there are no elements common to both sets.
Intersection has several properties similar to conjunction:
- Commutativity: A ∩ B = B ∩ A.
- Associativity: (A ∩ B) ∩ C = A ∩ (B ∩ C).
- Distributivity over union: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).
- Idempotence: A ∩ A = A.
- Identity element: A ∩ U = A, where U is the universal set.
- Absorbing element: A ∩ ∅ = ∅.
- Complement law: A ∩ A’ = ∅.
Conjunction in a Logic Circuit
Logical conjunction is an important concept in the field of digital circuits and is implemented using the AND gate, a crucial electronic component for the operation of various computational systems. This concept comes from Boolean algebra, a branch of mathematics that focuses on logical operations and is fundamental to the design of digital circuits.
An AND gate takes two or more input signals and produces an output that is true (1) only if all inputs are true (1). If any of the inputs is false (0), the output will be false (0).
AND gates have several applications in digital circuits, including:
- Implementation of logical functions: AND gates are combined to create circuits that perform various logical functions, such as comparators, decoders, and multiplexers.
- Construction of arithmetic units: Basic arithmetic units, such as for addition and subtraction, can be built using AND gates in combination with other logic gates.
- Design of control systems: AND gates are used in control systems to implement logical conditions that determine the system's behavior.
Logical conjunction is often represented by specific operators that vary depending on the programming language. Some common examples are:
- C/C++: &&
- Java: &&
- Python: and
- JavaScript: &&
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

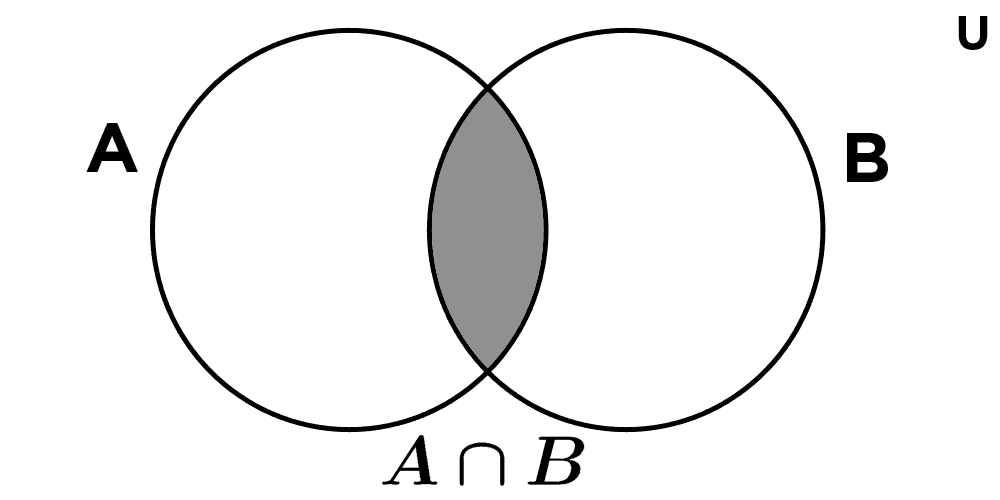
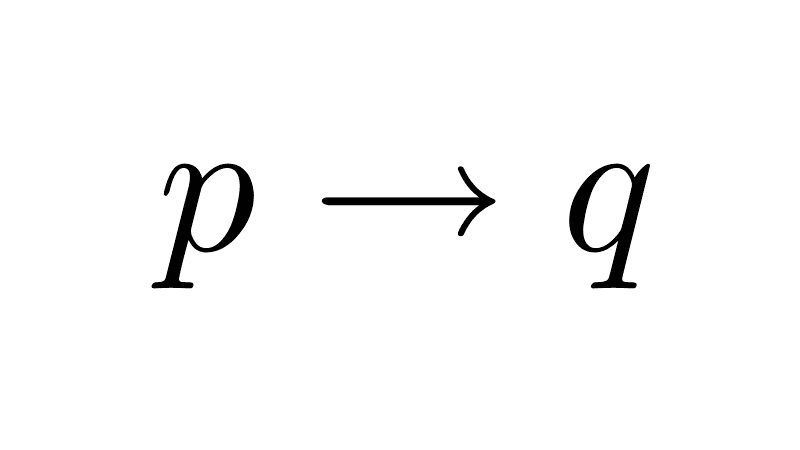
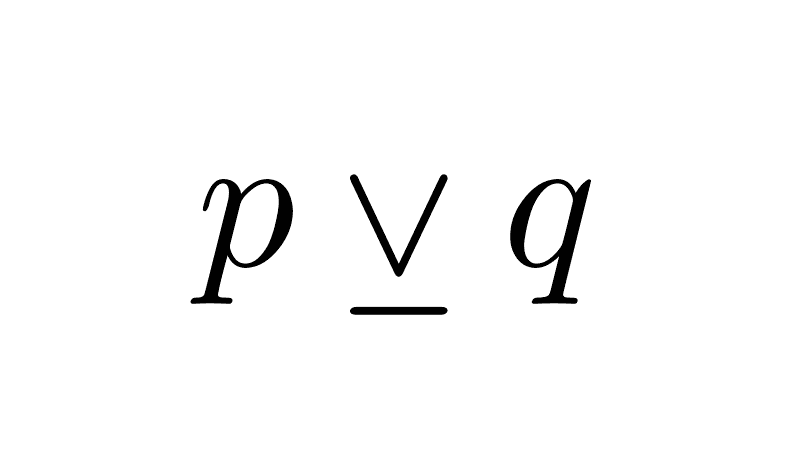
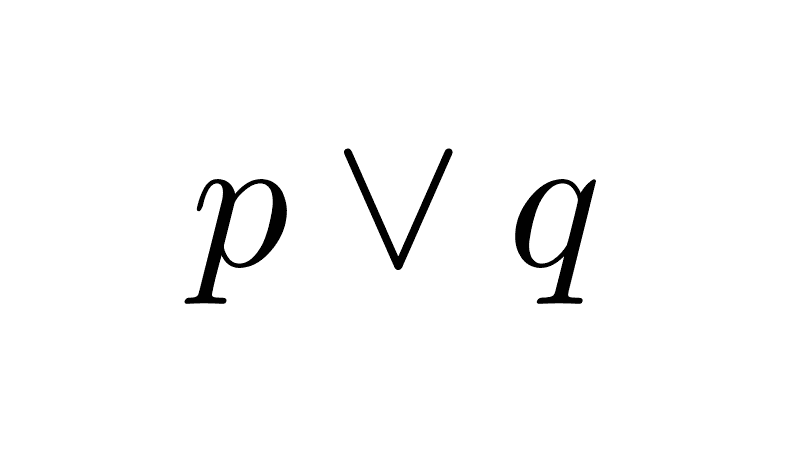
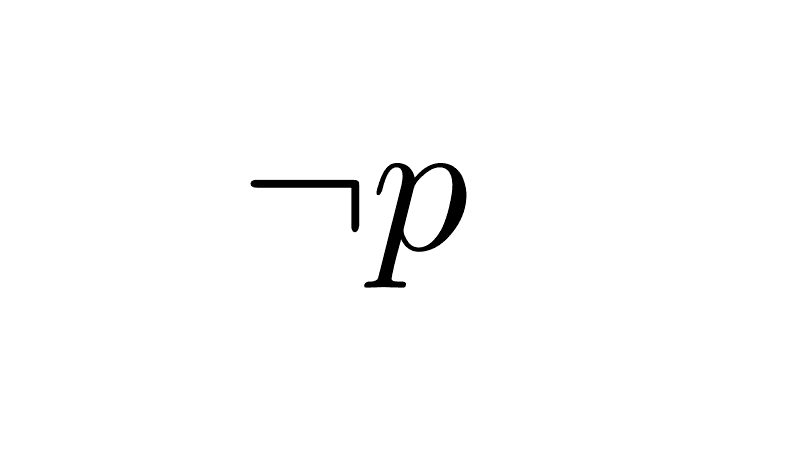
Related posts