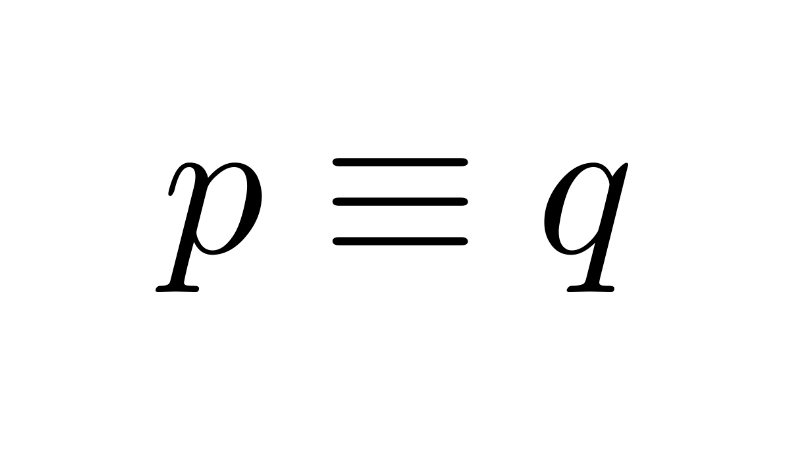
Logical Symbols
Logical symbols are characters used in mathematical logic to formally and precisely represent propositions, connectives, quantifiers, and relationships. These symbols allow us to structure arguments, prove theorems, and analyze the validity of reasoning.
To represent propositions, the letters p, q, r, s... are used.
| Symbol | Name | Meaning | Example |
|---|---|---|---|
| ¬ | Negation | "not" | ¬p ("not p") |
| ∧ | Conjunction | "and" | p ∧ q ("p and q") |
| ∨ | Inclusive disjunction | "or" (can be both) | p ∨ q ("p or q, or both") |
| ⊻ | Exclusive disjunction | "or" (but not both) | p ⊻ q ("p or q, but not both") |
| → | Conditional (Implication) | "if… then" | p → q ("if p, then q") |
| ↔ | Biconditional (Double implication) | "if and only if" | p ↔ q ("p if and only if q") |
| ∀ | Universal quantifier | "for all" | ∀x ∈ ℕ : x ≥ 0 ("every natural number is non-negative") |
| ∃ | Existential quantifier | "there exists at least one" | ∃x ∈ ℝ / x2 = 2 ("there exists a real number whose square is 2") |
| ∃! | Unique existential quantifier | "there exists only one" | ∃! x ∈ ℤ / 1 + x = 2 ("there exists only one integer which, when added to 1, results in 2") |
| ∄ | Negated existential quantifier | "there does not exist" | ∄ x ∈ ℚ / x2 = 2 ("there is no rational number whose square is 2") |
Leave a Reply

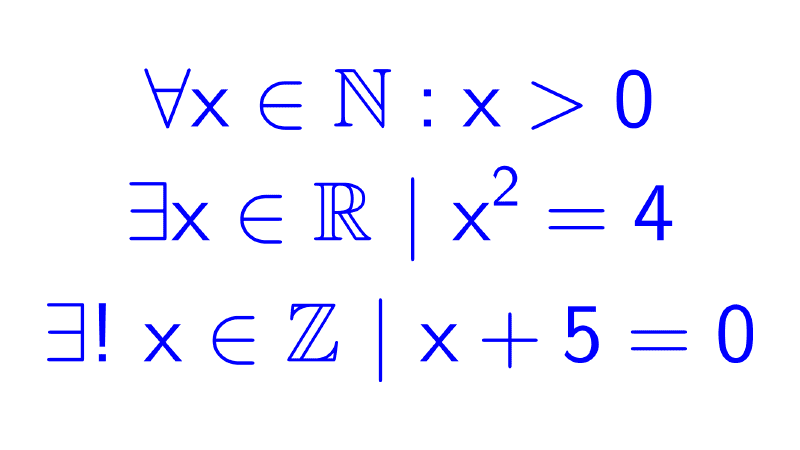
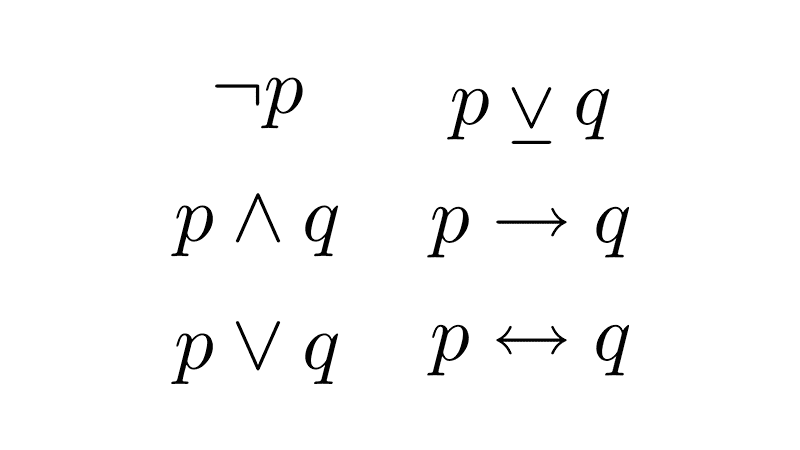
Related posts