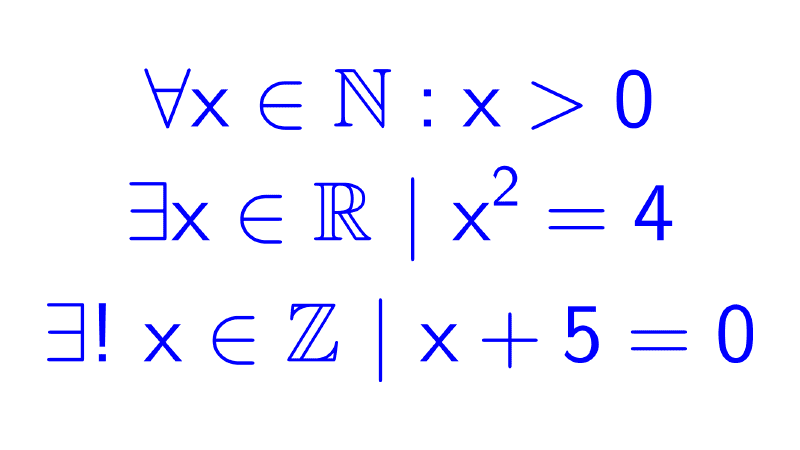
Logical Tautology
In propositional logic, a tautology or logical law is a compound proposition that is always true regardless of the truth values of the simple propositions that make it up.
For example, the following propositions are tautologies:
- p ∨ ¬p, also called the law of the excluded middle.
- ¬(p ∧ ¬p), called the law of non-contradiction.
- ¬(¬p) ↔ p, called the double negation law.
- (p ∧ q) → q, is a law of simplification.
- ¬(p ∧ q) ↔ ¬p ∨ ¬q, called De Morgan's law for conjunction.
- ¬(p ∨ q) ↔ ¬p ∧ ¬q, called De Morgan's law for disjunction.
Truth tables
To verify if a proposition is a tautology, one can construct a truth table. If the proposition's column turns out to be true for all possible combinations of the variables' truth values, then the proposition is a tautology.
Example 1
The truth table for the law of the excluded middle, p ∨ ¬p, is:
| p | ¬p | p ∨ ¬p |
|---|---|---|
| T | F | T |
| F | T | T |
Note that the last column, for the original proposition, only has true values.
Example 2
We can construct the truth table for the double negation law, ¬(¬p) ↔ p:
| p | ¬p | ¬(¬p) | ¬(¬p) ↔ p |
|---|---|---|---|
| T | F | T | T |
| F | T | F | T |
Example 3
The truth table for (p ∧ q) → q shows that it is a tautology:
| p | q | p ∧ q | (p ∧ q) → q |
|---|---|---|---|
| T | T | T | T |
| T | F | F | T |
| F | T | F | T |
| F | F | F | T |
Example 4
The following is the truth table for De Morgan's law for conjunction, ¬(p ∧ q) ↔ ¬p ∨ ¬q:
| p | q | ¬p | ¬q | p ∧ q | ¬(p ∧ q) | ¬p ∨ ¬q | ¬(p ∧ q) ↔ ¬p ∨ ¬q |
|---|---|---|---|---|---|---|---|
| T | T | F | F | T | F | F | T |
| T | F | F | T | F | T | T | T |
| F | T | T | F | F | T | T | T |
| F | F | T | T | F | T | T | T |
Tautologies differ from contingencies, which are propositions that can be true or false depending on the truth values of the simple propositions. Tautological propositions are also the opposite of contradictions, which are always false. Every tautology is the negation of a contradiction.
To obtain the tautology associated with a contradiction, it is sufficient to negate that proposition. Thus, for example, the negation of the contradiction p ∧ ¬p is ¬(p ∧ ¬p), which is the law of non-contradiction, a tautology.
Tautologies are fundamental in symbolic logic because they allow, among other things:
- Demonstrate the validity of arguments: if an argument can be shown to be a tautology, it means it is valid in all possible interpretations.
- Help simplify logical expressions: they can be used to rewrite or simplify more complex logical expressions.
- Design logic circuits: tautologies can be used to create logic circuits that always produce the correct result, regardless of the inputs.
Bibliography
- Epp, S. (2020). Discrete Mathematics with Applications (5th ed.). Cengage.
- Gallier, J., & Quaintance, J. (2025). Mathematical foundations and aspects of discrete mathematics.
- Haggard, G., Schlipf, J., & Whitesides, S. (2006). Discrete mathematics for computer science. Thomson Brooks/Cole.
- Hunter, D. (2017). Essentials of discrete mathematics (3rd ed.). Jones & Bartlett Learning.
- Johnsonbaugh, R. (2018). Discrete Mathematics (8th ed.). Pearson.
- Levin, O. (2024). Discrete mathematics: An open introduction (4th ed.).
- Lipschutz, S., & Lipson, M. (2007). Theory and problems of discrete mathematics (3rd ed.). McGraw-Hill.
Leave a Reply

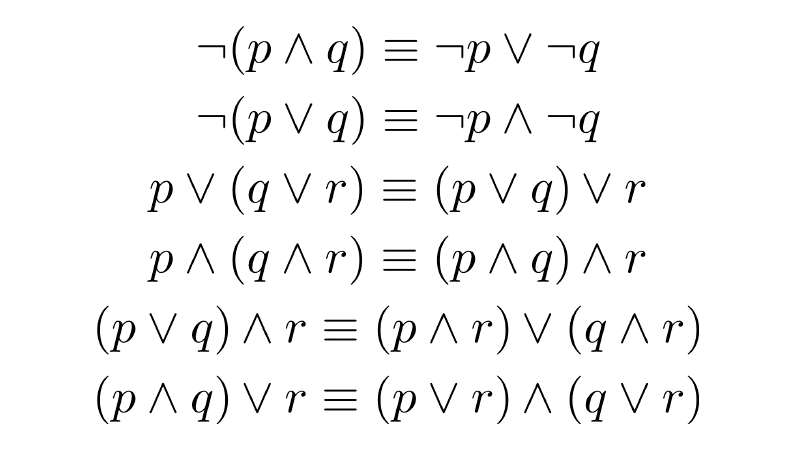
Related posts